11.1 एक लम्बवृत्तीय शंकु का पृष्ठीय क्षेत्रफल

हम पहले ही घन, घनाभ और बेलन के पृष्ठीय क्षेत्रफलों का अध्ययन कर चुके हैं। अब हम शंकु के पृष्ठीय क्षेत्रफल का अध्ययन करेंगे।
अब तक हम सर्वांगसम आकृतियों को एक के ऊपर एक चढ़ाकर ठोस बनाते आए हैं। संयोगवश ऐसी आकृतियों को प्रिज़्म कहा जाता है। अब आइए एक अन्य प्रकार के ठोस की ओर देखें जो प्रिज़्म नहीं होता (इस प्रकार के ठोसों को पिरामिड कहा जाता है)। आइए देखें कि हम उन्हें कैसे बना सकते हैं।

गतिविधि : एक समकोण त्रिभुज $\mathrm{ABC}$ काटें जो $\mathrm{B}$ पर समकोण है। त्रिभुज की एक लम्बवत् भुजा, मान लीजिए AB, के साथ एक मोटा लंबा डोर चिपकाएं [देखें आकृति 11.1(a)]। डोर को त्रिभुज के दोनों ओर अपने हाथों से पकड़ें और त्रिभुज को डोर के चारों ओर कई बार घुमाएं। क्या होता है? क्या आप वह आकृति पहचानते हैं जो त्रिभुज डोर के चारों ओर घूमते हुए बना रहा है [देखें आकृति 11.1(b)]? क्या यह आपको उस समय की याद दिलाता है जब आपने आइस-क्रीम को उसी आकार के डिब्बे में ढेर करके खाया था [देखें आकृति 11.1(c) और (d)]?

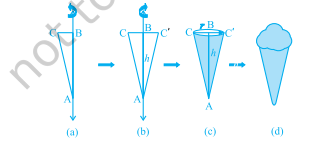
आकृति 11.1

इसे लम्ब वृत्तीय शंकु कहा जाता है। आकृति 11.1(c) के लम्ब वृत्तीय शंकु में बिंदु $\mathrm{A}$ शीर्ष कहलाता है, $\mathrm{AB}$ ऊँचाई कहलाती है, $\mathrm{BC}$ त्रिज्या कहलाती है और $AC$ शंकु की तिर्यक ऊँचाई कहलाती है। यहाँ $B$ शंकु के वृत्तीय आधार का केंद्र होगा। शंकु की ऊँचाई, त्रिज्या और तिर्यक ऊँचाई को सामान्यतः क्रमशः $h$, $r$ और $l$ से दर्शाया जाता है। एक बार फिर, आइए देखें कि हम किस प्रकार के शंकु को लम्ब वृत्तीय शंकु नहीं कह सकते। यह रहा आप (देखिए आकृति 11.2)! जो आप इन आकृतियों में देख रहे हैं वे लम्ब वृत्तीय शंकु नहीं हैं; क्योंकि (a) में, उसका शीर्ष जो आधार के केंद्र से जुड़ता है वह रेखा आधार पर लम्ब कोण पर नहीं है, और (b) में आधार वृत्ताकार नहीं है।

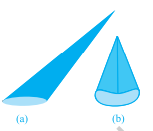
आकृति 11.2

जैसा कि बेलन के मामले में था, चूँकि हम केवल लम्ब वृत्तीय शंकुओं के बारे में पढ़ रहे हैं, याद रखिए कि इस अध्याय में ‘शंकु’ शब्द से हमारा तात्पर्य ‘लम्ब वृत्तीय शंकु’ से होगा।

गतिविधि : (i) एक साफ-सुथरा कागज़ का शंकु काटिए जिसमें कोई ओवरलैप्ड कागज़ न हो, उसे उसकी भुजा के साथ सीधा काटिए और खोलिए, ताकि यह देखा जा सके कि शंकु की सतह बनाने वाला कागज़ किस आकार का है। (जिस रेखा के साथ आप शंकु को काटते हैं वह शंकु की तिर्यक ऊँचाई है जिसे $l$ से दर्शाया गया है)। यह एक गोल केक के एक हिस्से जैसा दिखता है।

(ii) यदि आप अब सिरों पर चिह्नित A और B भुजाओं को एक साथ लाते हैं, तो आप देख सकते हैं कि आकृति 11.3 (c) का वक्रित भाग शंकु के वृत्तीय आधार का निर्माण करेगा।

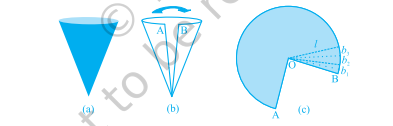
आकृति 11.3

(iii) यदि आकृति 11.3 (c) जैसे कागज़ को अब बिंदु $\mathrm{O}$ से खींची गई रेखाओं के साथ सैकड़ों छोटे टुकड़ों में काटा जाए, तो प्रत्येक कटा हुआ भाग लगभग एक छोटा त्रिभुज है, जिसकी ऊँचाई शंकु की तिर्यक ऊँचाई $l$ है।

(iv) अब प्रत्येक त्रिभुज का क्षेत्रफल $=\frac{1}{2} \times$ प्रत्येक त्रिभुज का आधार $\times l$।

इसलिए, पूरे कागज़ का क्षेत्रफल

$$ \begin{aligned} & =\text { सभी त्रिभुजों के क्षेत्रफलों का योग } \\ & =\frac{1}{2} b_{1} l+\frac{1}{2} b_{2} l+\frac{1}{2} b_{3} l+\cdots=\frac{1}{2} l\left(b_{1}+b_{2}+b_{3}+\cdots\right) \\ & =\frac{1}{2} \times l \times \text { आकृति 11.3(c) की संपूर्ण वक्र सीमा की लंबाई } \end{aligned} $$

$\quad$(चूँकि $b_{1}+b_{2}+b_{3}+\ldots$ आकृति के वक्रित भाग का निर्माण करता है)

परंतु आकृति का वक्रित भाग शंकु के आधार की परिधि बनाता है और शंकु के आधार की परिधि $=2 \pi r$, जहाँ $r$ शंकु की आधार त्रिज्या है।

इसलिए, शंकु का वक्र पृष्ठीय क्षेत्रफल $=\frac{1}{2} \times l \times 2 \pi r=\pi r l$

जहाँ $r$ इसकी आधार त्रिज्या है और $l$ इसकी तिर्यक ऊँचाई है।

ध्यान दें कि $l^{2}=r^{2}+h^{2}$ (जैसा कि चित्र 11.4 से देखा जा सकता है), पाइथागोरस प्रमेय लागू करने पर। यहाँ $h$ शंकु की ऊँचाई है।

इसलिए, $l=\sqrt{r^{2}+h^{2}}$

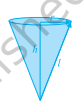
चित्र 11.4

अब यदि शंकु के आधार को बंद करना है, तो त्रिज्या $r$ का एक वृत्ताकार कागज़ का टुकड़ा भी चाहिए जिसका क्षेत्रफल $\pi r^{2}$ है।

इसलिए, शंकु का कुल पृष्ठीय क्षेत्रफल $=\pi r l+\pi r^{2}=\pi r(l+r)$

उदाहरण 1 : एक लंब वृत्ताकार शंकु का वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए जिसकी तिर्यक ऊँचाई $10 \mathrm{~cm}$ है और आधार की त्रिज्या $7 \mathrm{~cm}$ है।

हल : वक्र पृष्ठीय क्षेत्रफल $=\pi r l$

$$ \begin{aligned} & =\frac{22}{7} \times 7 \times 10 \mathrm{~cm}^{2} \\ & =220 \mathrm{~cm}^{2} \end{aligned} $$

उदाहरण 2 : एक शंकु की ऊँचाई $16 \mathrm{~cm}$ है और इसकी आधार की त्रिज्या $12 \mathrm{~cm}$ है। शंकु का वक्र पृष्ठीय क्षेत्रफल और कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए ($\pi=3.14$ प्रयोग कीजिए)।

हल : यहाँ, $h=16 \mathrm{~cm}$ और $r=12 \mathrm{~cm}$।

इसलिए, $l^{2}=h^{2}+r^{2}$ से, हमें मिलता है

$$ l=\sqrt{16^{2}+12^{2}} \mathrm{~cm}=20 \mathrm{~cm} $$

इसलिए, वक्र पृष्ठीय क्षेत्रफल $=\pi r l$

$$ \begin{aligned} & =3.14 \times 12 \times 20 \mathrm{~cm}^{2} \\ & =753.6 \mathrm{~cm}^{2} \end{aligned} $$

इसके अतिरिक्त, कुल पृष्ठीय क्षेत्रफल $=\pi r l+\pi r^{2}$

$$ \begin{aligned} & =(753.6+3.14 \times 12 \times 12) \mathrm{cm}^{2} \ & =(753.6+452.16) \mathrm{cm}^{2} \ & =1205.76 \mathrm{~cm}^{2} \end{aligned} $$

उदाहरण 3 : एक मकई की बाली (देखें चित्र 11.5), जो कि लगभग एक शंकु के आकार की होती है, के सबसे चौड़े सिरे की त्रिज्या $2.1 \mathrm{~cm}$ और लंबाई (ऊँचाई) $20 \mathrm{~cm}$ है। यदि बाली की सतह के प्रत्येक $1 \mathrm{~cm}^{2}$ पर औसतन चार दाने होते हैं, तो पूरी बाली पर कितने दाने पाए जाएंगे, यह ज्ञात कीजिए।

चित्र 11.5

हल : चूँकि मकई के दाने केवल मकई की बाली के वक्र सतह पर पाए जाते हैं, इसलिए उस पर कुल दानों की संख्या ज्ञात करने के लिए हमें बाली के वक्र सतह क्षेत्र की आवश्यकता होगी। इस प्रश्न में हमें शंकु की ऊँचाई दी गई है, इसलिए हमें उसकी तिर्यक ऊँचाई ज्ञात करनी होगी।

यहाँ, $\quad l=\sqrt{r^{2}+h^{2}}=\sqrt{(2.1)^{2}+20^{2}} \mathrm{~cm}$

$$ =\sqrt{404.41} \mathrm{~cm}=20.11 \mathrm{~cm} $$

इसलिए, मकई की बाली का वक्र सतह क्षेत्र $=\pi r l$

$$ =\frac{22}{7} \times 2.1 \times 20.11 \mathrm{~cm}^{2}=132.726 \mathrm{~cm}^{2}=132.73 \mathrm{~cm}^{2} \text { (लगभग) } $$

मकई की बाली की सतह के $1 \mathrm{~cm}^{2}$ पर मकई के दानों की संख्या $=4$

इसलिए, बाली की पूरी वक्र सतह पर दानों की संख्या

$$ =132.73 \times 4=530.92=531 \text { (लगभग) } $$

इसलिए, मकई के भुट्टे पर लगभग 531 दाने होंगे।

11.2 एक गोले का पृष्ठीय क्षेत्रफल

गोला क्या होता है? क्या यह वृत्त के समान होता है? क्या आप कागज़ पर वृत्त बना सकते हैं? हाँ, आप बना सकते हैं, क्योंकि वृत्त एक समतलीय बंद आकृति होती है जिसका प्रत्येक बिंदु एक निश्चित बिंदु, जिसे वृत्त का केंद्र कहा जाता है, से एक नियत दूरी (जिसे त्रिज्या कहा जाता है) पर स्थित होता है। अब यदि आप एक वृत्ताकार डिस्क के व्यास के साथ एक डोरी चिपकाएँ और उसे घुमाएँ जैसे आपने पिछले भाग में त्रिभुज घुमाया था, तो आपको एक नई ठोस आकृति दिखाई देती है (देखिए चित्र 11.6)। यह किससे मिलती-जुलती है? एक गेंद से? हाँ। इसे गोला कहा जाता है।

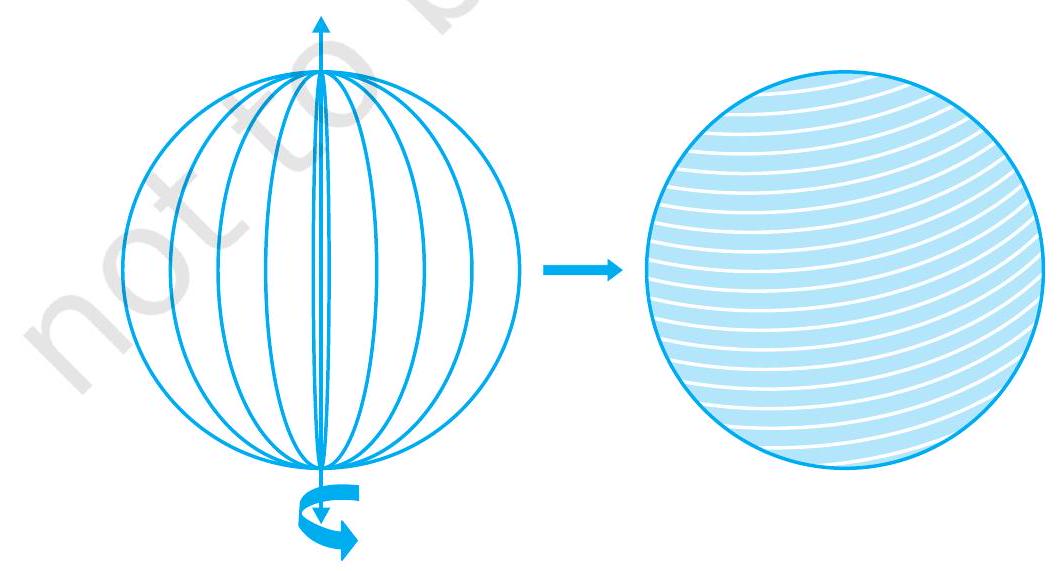
चित्र 11.6

क्या आप अनुमान लगा सकते हैं कि वृत्त का केंद्र घूमने पर गोला बनाते समय क्या बन जाता है? निश्चित ही, यह गोले का केंद्र बन जाता है। इसलिए, एक गोला एक त्रिविमीय आकृति (ठोस आकृति) होता है, जो उन सभी बिंदुओं से बना होता है जो अंतरिक्ष में एक निश्चित बिंदु, जिसे गोले का केंद्र कहा जाता है, से एक नियत दूरी, जिसे त्रिज्या कहा जाता है, पर स्थित होते हैं।

नोट : एक गोला एक गेंद की सतह के समान होता है। ठोस गोले शब्द का प्रयोग उस ठोस के लिए किया जाता है जिसकी सतह एक गोला होता है।

गतिविधि : क्या आपने कभी लट्टू खेला है या कम-से-कम किसी को लट्टू खेलते हुए देखा है? आपको यह तो पता ही होगा कि उसके चारों ओर डोरी कैसे लपेटी जाती है। अब हम एक रबर की गेंद लें और उसमें एक कील गाड़ दें। कील का सहारा लेकर गेंद के चारों ओर डोरी लपेटें। जब आप गेंद के ‘सबसे चौड़े’ हिस्से तक पहुँच जाएँ, तो डोरी को वहीं रोकने के लिए पिन लगा दें और बाकी बचे हिस्से को भी डोरी से ढकते हुए आगे बढ़ें, जब तक कि पूरी गेंद ढक न जाए [देखें चित्र 11.7(a)]। डोरी पर शुरुआत और खत्म होने की जगह चिह्नित करें और फिर धीरे-धीरे डोरी को गेंद की सतह से खोल लें।

अब अपने शिक्षक से कहें कि वे गेंद का व्यास मापने में आपकी मदद करें, जिससे आप आसानी से उसकी त्रिज्या निकाल सकें। फिर एक कागज़ की शीट पर, गेंद की त्रिज्या के बराबर त्रिज्या वाले चार वृत्त बनाएँ। इन वृत्तों को एक-एक करके उस डोरी से भरना शुरू करें, जो आपने गेंद के चारों ओर लपेटी थी [देखें चित्र 11.7(b)]।

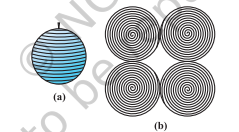
चित्र 11.7

इन सबसे आपने क्या हासिल किया?

वह डोरी, जिसने गोले की संपूर्ण सतह को ढक लिया था, का उपयोग करके चार वृत्तों—जिनकी त्रिज्या गोले की त्रिज्या के बराबर है—के क्षेत्रों को पूरी तरह भर दिया गया।

तो इसका क्या अर्थ है? इससे संकेत मिलता है कि त्रिज्या $r$ वाले गोले का पृष्ठीय क्षेत्रफल $=4$ गुना उस वृत्त का क्षेत्रफल जिसकी त्रिज्या $r$ है $=4 \times\left(\pi r^{2}\right)$

इसलिए, $\quad$एक गोले का पृष्ठीय क्षेत्रफल $=4 \pi r^{2}$

जहाँ $r$ गोले की त्रिज्या है।

आप एक गोले की सतह में कितने फलक देखते हैं? इसमें केवल एक ही है, जो वक्र होता है।

अब, आइए एक ठोस गोले को लें, और इसे ठीक ‘बीच से’ इस तरह काटें कि वह तल इसके केंद्र से होकर गुजरे। गोले को क्या होता है?

हाँ, यह दो बराबर भागों में बंट जाता है (देखिए चित्र 11.8)! प्रत्येक आधे भाग को क्या कहा जाएगा? इसे अर्धगोला कहा जाता है। (क्योंकि ‘हेमी’ का अर्थ भी ‘आधा’ होता है)

चित्र 11.8

और अर्धगोले की सतह के बारे में क्या? इसमें कितने फलक होते हैं?

दो! इसमें एक वक्र फलक और एक समतल फलक (आधार) होता है।

अर्धगोले का वक्र पृष्ठीय क्षेत्रफल गोले के पृष्ठीय क्षेत्रफल का आधा होता है, जो $4 \pi r^{2}$ का $\frac{1}{2}$ है।

इसलिए, अर्धगोले का वक्र पृष्ठीय क्षेत्रफल $=\mathbf{2} \boldsymbol{\pi} r^{2}$

जहाँ $r$ उस गोले की त्रिज्या है जिसका एक भाग अर्धगोला है।

अब अर्धगोले के दोनों फलकों को लेते हुए, इसका पृष्ठीय क्षेत्रफल $2 \pi r^{2}+\pi r^{2}$

इसलिए, अर्धगोले का कुल पृष्ठीय क्षेत्रफल $=3 \pi r^{2}$

उदाहरण 4 : त्रिज्या $7 \mathrm{~cm}$ वाले गोले का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

हल : त्रिज्या $7 \mathrm{~cm}$ वाले गोले का पृष्ठीय क्षेत्रफल होगा

$$ 4 \pi r^{2}=4 \times \frac{22}{7} \times 7 \times 7 \mathrm{~cm}^{2}=616 \mathrm{~cm}^{2} $$

उदाहरण 5 : एक अर्धगोले की त्रिज्या $21 \mathrm{~cm}$ है, तो (i) वक्र पृष्ठीय क्षेत्रफल और (ii) कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

हल : त्रिज्या $21 \mathrm{~cm}$ वाले अर्धगोले का वक्र पृष्ठीय क्षेत्रफल

$$ =2 \pi r^{2}=2 \times \frac{22}{7} \times 21 \times 21 \mathrm{~cm}^{2}=2772 \mathrm{~cm}^{2} $$

(ii) अर्धगोले का कुल पृष्ठीय क्षेत्रफल होगा

$$ 3 \pi r^{2}=3 \times \frac{22}{7} \times 21 \times 21 \mathrm{~cm}^{2}=4158 \mathrm{~cm}^{2} $$

उदाहरण 6 : सर्कस के मोटरसाइकिल चालक जिस खोखले गोले में अपने करतब दिखाता है, उसका व्यास $7 \mathrm{~m}$ है। चालक के चलने के लिए उपलब्ध क्षेत्रफल ज्ञात कीजिए।

हल : गोले का व्यास $=7 \mathrm{~m}$। इसलिए, त्रिज्या $3.5 \mathrm{~m}$ है। अतः मोटरसाइकिल चालक के लिए उपलब्ध राइडिंग स्थान ‘गोले’ का पृष्ठीय क्षेत्रफल है, जो कि

$$ \begin{aligned} 4 \pi r^{2} & =4 \times \frac{22}{7} \times 3.5 \times 3.5 \mathrm{~m}^{2} \ & =154 \mathrm{~m}^{2} \end{aligned} $$

उदाहरण 7 : एक इमारत के अर्धगोलाकार गुंबद को पेंट करना है (देखिए आकृति 11.9)। यदि गुंबद के आधार की परिधि $17.6 \mathrm{~m}$ है, तो इसे पेंट करने की लागत ज्ञात कीजिए, यदि पेंटिंग की दर ₹ 5 प्रति $100 \mathrm{~cm}^{2}$ है।

चित्र 11.9

हल : चूँकि गुंबद की केवल गोलाकार सतह को पेंट किया जाना है, हमें गोलार्ध के वक्र पृष्ठीय क्षेत्रफल को ज्ञात करना होगा ताकि यह जाना जा सके कि कितने क्षेत्रफल पर पेंट करना है। अब, गुंबद की परिधि = 17.6 m। इसलिए, 17.6 = 2πr।

अतः, गुंबद की त्रिज्या = 17.6 × 7/(2 × 22) m = 2.8 m

गुंबद का वक्र पृष्ठीय क्षेत्रफल = 2πr²

$$ \begin{aligned} & = 2 × \frac{22}{7} × 2.8 × 2.8 \text{ m²} \ & = 49.28 \text{ m²} \end{aligned} $$

अब, 100 cm² पेंट करने की लागत ₹5 है।

इसलिए, 1 m² पेंट करने की लागत = ₹500

अतः, पूरे गुंबद को पेंट करने की लागत = ₹500 × 49.28 = ₹24640

11.3 एक लंब वृत्तीय शंकु का आयतन

पिछली कक्षाओं में हम घन, घनाभ और बेलन के आयतनों का अध्ययन कर चुके हैं

चित्र 11.11 में, क्या आप देख सकते हैं कि एक लंब वृत्तीय बेलन और एक लंब वृत्तीय शंकु हैं जिनकी आधार त्रिज्या और ऊँचाई समान हैं?

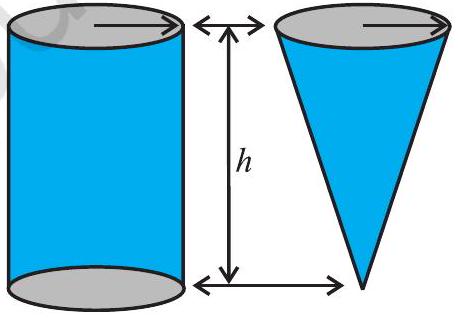
चित्र 11.11

गतिविधि : कोशिश करें कि एक खोखला बेलन और एक खोखला शंकु इसी तरह बनाएँ जिनकी आधार त्रिज्या और ऊँचाई समान हों (देखें आकृति 11.11)। फिर हम एक प्रयोग कर सकते हैं जो व्यावहारिक रूप से दिखाएगा कि एक लंब वृत्तीय शंकु का आयतन कितना होता है!

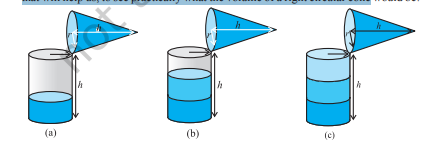
आकृति 11.12

तो चलिए इस तरह शुरू करते हैं।

शंकु को एक बार ऊपर तक रेत से भरें और उसे बेलन में खाली कर दें। हम पाते हैं कि यह बेलन का केवल एक भाग ही भरता है [देखें आकृति 11.12(a)]।

जब हम शंकु को फिर से ऊपर तक भरते हैं और उसे बेलन में खाली करते हैं, तो देखते हैं कि बेलन अब भी पूरा नहीं भरा [देखें आकृति 11.12(b)]।

जब शंकु को तीसरी बार भरा जाता है और बेलन में खाली किया जाता है, तो देखा जा सकता है कि बेलन भी ऊपर तक भर गया है [देखें आकृति 11.12(c)]।

इससे हम निश्चित रूप से निष्कर्ष निकाल सकते हैं कि शंकु का आयतन तीन गुना करने पर वह बेलन के आयतन के बराबर होता है, जिसकी आधार त्रिज्या और ऊँचाई शंकु के समान है, जिसका अर्थ है कि शंकु का आयतन बेलन के आयतन का एक-तिहाई होता है।

इसलिए, $\quad \text { एक शंकु का आयतन }=\frac{1}{3} \pi r^{2} h$

जहाँ $r$ आधार त्रिज्या है और $h$ शंकु की ऊँचाई है।

उदाहरण 8 : एक शंकु की ऊँचाई और तिर्यक ऊँचाई क्रमशः $21 \mathrm{~cm}$ और $28 \mathrm{~cm}$ हैं। शंकु का आयतन ज्ञात कीजिए।

हल : $l^{2}=r^{2}+h^{2}$ से, हम पाते हैं

$$ r=\sqrt{l^{2}-h^{2}}=\sqrt{28^{2}-21^{2}} \mathrm{~cm}=7 \sqrt{7} \mathrm{~cm} $$

अतः, शंकु का आयतन $=\frac{1}{3} \pi r^{2} h=\frac{1}{3} \times \frac{22}{7} \times 7 \sqrt{7} \times 7 \sqrt{7} \times 21 \mathrm{~cm}^{3}$

$=7546 \mathrm{~cm}^{3}$

उदाहरण 9 : मोनिका के पास कैनवास का एक टुकड़ा है जिसका क्षेत्रफल $551 \mathrm{~m}^{2}$ है। वह इसका उपयोग एक शंक्वाकार तम्बू बनाने के लिए करती है, जिसकी आधार त्रिज्या $7 \mathrm{~m}$ है। यह मानते हुए कि सिलाई के किनारे और काटने के दौरान होने वाली बर्बादी लगभग $1 \mathrm{~m}^{2}$ है, उस तम्बू का आयतन ज्ञात कीजिए जो इससे बनाया जा सकता है।

हल : चूँकि कैनवास का क्षेत्रफल $=551 \mathrm{~m}^{2}$ है और बर्बादी में खोया गया कैनवास का क्षेत्रफल $1 \mathrm{~m}^{2}$ है, इसलिए तम्बू बनाने के लिए उपलब्ध कैनवास का क्षेत्रफल $(551-1) \mathrm{m}^{2}=550 \mathrm{~m}^{2}$ है।

अब, तम्बू का पृष्ठीय क्षेत्रफल $=550 \mathrm{~m}^{2}$ है और शंक्वाकार तम्बू के लिए आवश्यक आधार त्रिज्या $=7 \mathrm{~m}$ है।

ध्यान दें कि एक तम्बू में केवल वक्र पृष्ठ होता है (तम्बू की फर्श कैनवास से ढकी नहीं होती!!)।

इसलिए, तम्बू का वक्र पृष्ठीय क्षेत्रफल $=550 \mathrm{~m}^{2}$ है।

अर्थात,$\quad \pi r l=550$

या,$\quad \frac{22}{7}\times 7 \times l=550$

या,$\quad l=3 \frac{550}{22} \mathrm{~m}=25 \mathrm{~m}$

अब,$\quad l^{2}=r^{2}+h^{2}$

$$ \begin{aligned} \text{इसलिए,}\quad h=\sqrt{l^{2}-r^{2}} & =\sqrt{25^{2}-7^{2}} \mathrm{~m}=\sqrt{625-49} \mathrm{~m}=\sqrt{576} \mathrm{~m} \\ & =24 \mathrm{~m} \end{aligned} $$

अतः शंक्वाकार तंबू का आयतन $=\frac{1}{3} \pi r^{2} h=\frac{1}{3} \times \frac{22}{7} \times 7 \times 7 \times 24 \mathrm{~m}^{3}=1232 \mathrm{~m}^{3}$ है।

11.4 गोले का आयतन

अब आइए देखें कि गोले का आयतन मापने के बारे में कैसे आगे बढ़ें। सबसे पहले, विभिन्न त्रिज्याओं के दो या तीन गोले लें, और एक ऐसा पात्र लें जो पर्याप्त बड़ा हो ताकि प्रत्येक गोले को एक समय में उसमें रखा जा सके। साथ ही, एक बड़ा ट्रफ लें जिसमें आप पात्र को रख सकें। फिर, पात्र को पानी से ऊपर तक भर दें [देखें चित्र 11.13(a)]।

अब, सावधानी से गोलों में से एक को पात्र में रखें। पात्र में से कुछ पानी ट्रफ में जिसमें यह रखा गया है, में बह जाएगा [देखें चित्र 11.13(b)]। ट्रफ से पानी को सावधानी से मापन सिलिंडर (अर्थात् एक ग्रेजुएटेड बेलनाकार जार) में डालें और बह गए पानी को मापें [देखें चित्र 11.13(c)]। मान लीजिए डूबे हुए गोले की त्रिज्या $r$ है (आप गोले के व्यास को मापकर त्रिज्या ज्ञात कर सकते हैं)। फिर $\frac{4}{3} \pi r^{3}$ का मूल्यांकन करें। क्या आपको यह मान बह गए आयतन के माप से लगभग बराबर लगता है?

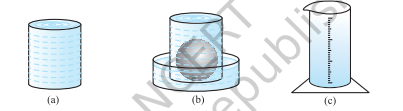
चित्र 11.13

एक बार फिर से अभी-अभी किए गए प्रक्रिया को दोहराएँ, गोले के एक भिन्न आकार के साथ। इस गोले की त्रिज्या $R$ ज्ञात कीजिए और फिर $\frac{4}{3} \pi R^{3}$ का मान निकालिए। एक बार फिर यह मान लगभग उसी जल के आयतन के बराबर है जो गोले द्वारा विस्थापित (बाहर बह गया) है। यह हमें क्या बताता है? हम जानते हैं कि गोले का आयतन उस जल के आयतन के बराबर होता है जिसे वह विस्थापित करता है। विभिन्न त्रिज्याओं वाले गोलों के साथ यह प्रयोग बार-बार करने पर हमें एक ही परिणाम मिलता है, अर्थात् गोले का आयतन उसकी त्रिज्या के घन का $\frac{4}{3} \pi$ गुना होता है। यह हमें यह विचार देता है कि

$\quad$ गोले का आयतन $=\frac{4}{3} \pi r^{3}$

जहाँ $r$ गोले की त्रिज्या है।

बाद में, उच्च कक्षाओं में इसे सिद्ध भी किया जा सकता है। परंतु इस स्तर पर हम इसे सत्य मान लेंगे।

चूँकि अर्धगोला एक गोले का आधा होता है, क्या आप अनुमान लगा सकते हैं कि अर्धगोले का आयतन क्या होगा? हाँ, यह $\frac{4}{3} \pi r^{3}$ का $\frac{1}{2}$ होता है $=\frac{2}{3} \pi r^{3}$।

इसलिए, $\quad$ अर्धगोले का आयतन $=\frac{\mathbf{2}}{\mathbf{3}} \pi r^{3}$

जहाँ $r$ अर्धगोले की त्रिज्या है।

आइए इन सूत्रों के प्रयोग को दर्शाने के लिए कुछ उदाहरण लें।

उदाहरण 10 : त्रिज्या $11.2 \mathrm{~cm}$ वाले गोले का आयतन ज्ञात कीजिए।

हल : अभीष्ट आयतन $=\frac{4}{3} \pi r^{3}$

$$ =\frac{4}{3} \times \frac{22}{7} \times 11.2 \times 11.2 \times 11.2 \mathrm{~cm}^{3}=5887.32 \mathrm{~cm}^{3} $$

उदाहरण 11 : एक शॉट-पुट एक धातु का गोला है जिसकी त्रिज्या $4.9 \mathrm{~cm}$ है। यदि धातु का घनत्व $7.8 \mathrm{~g} \mathrm{per} \mathrm{cm}^{3}$ हो, तो शॉट-पुट का द्रव्यमान ज्ञात कीजिए।

हल : चूँकि शॉट-पुट एक ठोस धातु का गोला है और इसका द्रव्यमान इसके आयतन और घनत्व के गुणनफल के बराबर होता है, हमें गोले का आयतन ज्ञात करना होगा।

अब, गोले का आयतन $=\frac{4}{3} \pi r^{3}$

$$ \begin{aligned} & =\frac{4}{3} \times \frac{22}{7} \times 4.9 \times 4.9 \times 4.9 \mathrm{~cm}^{3} \\ & =493 \mathrm{~cm}^{3} \text { (लगभग) } \end{aligned} $$

आगे, $1 \mathrm{~cm}^{3}$ धातु का द्रव्यमान $7.8 \mathrm{~g}$ है।

इसलिए, शॉट-पुट का द्रव्यमान $=7.8 \times 493 \mathrm{~g}$

$$ =3845.44 \mathrm{~g}=3.85 \mathrm{~kg} \text { (लगभग) } $$

उदाहरण 12 : एक अर्धगोलाकार कटोरे की त्रिज्या $3.5 \mathrm{~cm}$ है। इसमें आया जा सकने वाले पानी का आयतन क्या होगा?

हल : कटोरे में आया जा सकने वाले पानी का आयतन

$$ \begin{aligned} & =\frac{2}{3} \pi r^{3} \\ & =\frac{2}{3} \times \frac{22}{7} \times 3.5 \times 3.5 \times 3.5 \mathrm{~cm}^{3}=89.8 \mathrm{cm}^{3} \end{aligned} $$

11.5 सारांश

इस अध्याय में, आपने निम्नलिखित बिंदुओं का अध्ययन किया है:

1. शंकु का वक्र पृष्ठीय क्षेत्रफल $=\pi r l$

2. लंब वृत्तीय शंकु का कुल पृष्ठीय क्षेत्रफल $=\pi r l +\pi r^{2}$, अर्थात् $\pi r(l+r)$

3. त्रिज्या $r$ वाले गोले का पृष्ठीय क्षेत्रफल $=4 \pi r^{2}$

4. अर्धगोले का वक्र पृष्ठीय क्षेत्रफल $=2 \pi r^{2}$

5. अर्धगोले का कुल पृष्ठीय क्षेत्रफल $=3 \pi r^{2}$

6. शंकु का आयतन $=\frac{1}{3} \pi r^{2} h$

7. त्रिज्या $r$ वाले गोले का आयतन $=\frac{4}{3} \pi r^{3}$

8. अर्धगोले का आयतन $=\frac{2}{3} \pi r^{3}$

[यहाँ अक्षर $l, b, h, a, r$ आदि अपने सामान्य अर्थों में प्रयोग किए गए हैं, संदर्भ के अनुसार।]