अध्याय 09 वृत्त
9.1 एक जीवा द्वारा किसी बिंदु पर अंतरित कोण
आपने पहले ही छठी कक्षा में वृत्त और उसके भागों के बारे में पढ़ा है।
एक रेखाखंड PQ लीजिए और एक बिंदु R जो PQ को सम्मिलित करने वाली रेखा पर नहीं है। PR और QR को मिलाइए (देखिए चित्र 9.1)। तब $\angle \mathrm{PRQ}$ को रेखाखंड $\mathrm{PQ}$ द्वारा बिंदु $\mathrm{R}$ पर अंतरित कोण कहा जाता है।
चित्र 9.2 में कोण POQ, PRQ और PSQ को क्या कहा जाता है? $\angle$ POQ वह कोण है जो जीवा $\mathrm{PQ}$ केंद्र $\mathrm{O}$ पर अंतरित करती है, $\angle \mathrm{PRQ}$ और $\angle \mathrm{PSQ}$ क्रमशः $\mathrm{PQ}$ द्वारा बड़े और छोटे चाप $\mathrm{PQ}$ पर स्थित बिंदुओं $\mathrm{R}$ और $\mathrm{S}$ पर अंतरित कोण हैं।

चित्र 9.1
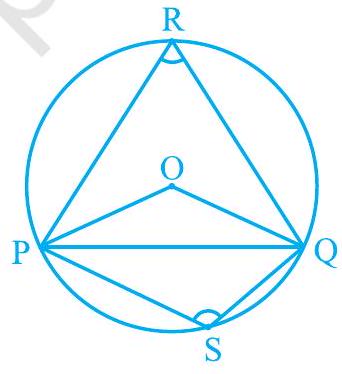
चित्र 9.2
आइए जांचते हैं कि जीवा के आकार और केंद्र पर इसके द्वारा अंतरित कोण के बीच क्या संबंध है। आप एक वृत्त की विभिन्न जीवाएँ खींचकर और उनके द्वारा केंद्र पर अंतरित कोणों को देखकर यह अनुभव कर सकते हैं कि जितनी लंबी जीवा होगी, उतना ही बड़ा कोण वह केंद्र पर अंतरित करेगी। यदि आप एक वृत्त की दो समान जीवाएँ लें तो क्या होगा? क्या केंद्र पर अंतरित कोण समान होंगे या नहीं?
एक वृत्त की दो या अधिक समान जीवाएँ खींचिए और उनके द्वारा केंद्र पर अंतरित कोणों को मापिए (देखिए आकृति 9.3)। आप पाएँगे कि वे सभी केंद्र पर समान कोण अंतरित करती हैं। आइए इस तथ्य का प्रमाण दें।
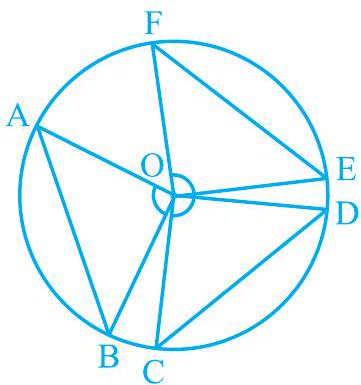
आकृति 9.3
प्रमेय 9.1 : एक वृत्त की समान जीवाएँ केंद्र पर समान कोण अंतरित करती हैं।
प्रमाण : आपको एक वृत्त की दो समान जीवाएँ AB और CD दी गई हैं जिसका केंद्र O है (देखिए आकृति 9.4)। आपको यह सिद्ध करना है कि $\angle \mathrm{AOB}=\angle \mathrm{COD}$
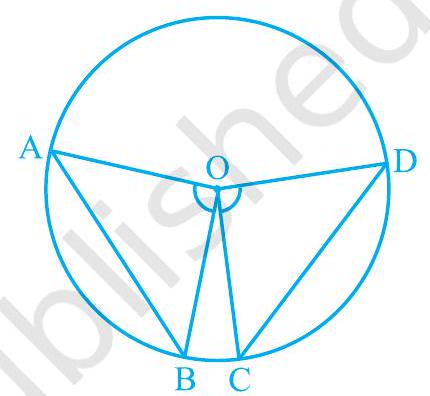
आकृति 9.4
त्रिभुजों $\mathrm{AOB}$ और $\mathrm{COD}$ में,
$$ \begin{array}{ll} \mathrm{OA}=\mathrm{OC} & (\text { एक वृत्त की त्रिज्याएँ }) \\ \mathrm{OB}=\mathrm{OD} & (\text { एक वृत्त की त्र�्याएँ }) \\ \mathrm{AB}=\mathrm{CD} & (\text { दिया है }) \end{array} $$
इसलिए
$$ \Delta \mathrm{AOB} \cong \Delta \mathrm{COD} \quad(\mathrm{SSS} \text { नियम }) $$
इससे प्राप्त होता है $\angle \mathrm{AOB}=\angle \mathrm{COD}$
(सर्वांगसम त्रिभुजों के संगत भाग)
टिप्पणी : सुविधा के लिए, संक्षेप में CPCT का प्रयोग ‘सर्वांगसम त्रिभुजों के संगत भाग’ के स्थान पर किया जाएगा, क्योंकि हम इसे बहुधा प्रयोग करेंगे जैसा कि आप देखेंगे।
अब यदि एक वृत्त की दो जीवाएँ केंद्र पर समान कोण बनाती हैं, तो आप उन जीवाओं के बारे में क्या कह सकते हैं? क्या वे समान हैं या नहीं? आइए इसे निम्नलिखित क्रियाकलाप द्वारा जाँचें:
एक ट्रेसिंग पेपर लें और उस पर एक वृत्त ट्रेस करें। वृत्त के साथ काटकर एक डिस्क प्राप्त करें। इसके केंद्र $\mathrm{O}$ पर एक कोण $\mathrm{AOB}$ बनाएँ जहाँ $\mathrm{A}, \mathrm{B}$ वृत्त पर बिंदु हैं। केंद्र पर एक अन्य कोण $\mathrm{POQ}$ बनाएँ जो $\angle A O B$ के समान हो। डिस्क को $A B$ और $P Q$ के साथ काटें (देखें चित्र 9.5)। आपको वृत्त के दो खंड ACB और PRQ प्राप्त होंगे। यदि आप एक को दूसरे पर रखें, तो आप क्या देखते हैं? वे एक-दूसरे को ढक लेते हैं, अर्थात् वे सर्वांगसम हैं। $\mathrm{इसलिए} \mathrm{AB}=\mathrm{PQ}$।
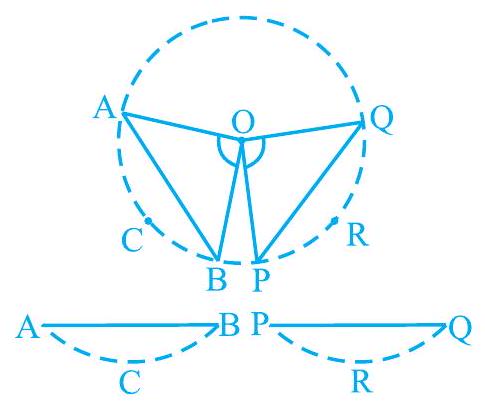
चित्र 9.5
हालाँकि आपने इस विशेष स्थिति में इसे देखा है, इसे अन्य समान कोणों पर भी आज़माएँ। निम्नलिखित प्रमेय के कारण सभी जीवाएँ समान सिद्ध होंगी:
प्रमेय 9.2: यदि किसी वृत्त की जीवाओं द्वारा केंद्र पर अंतरित कोण समान हों, तो जीवाएँ समान होती हैं।
उपरोक्त प्रमेय प्रमेय 9.1 का व्युत्क्रम है। ध्यान दें कि चित्र 9.4 में, यदि आप $\angle \mathrm{AOB}=\angle \mathrm{COD}$ लें, तो
$\triangle \mathrm{AOB} \cong \triangle \mathrm{COD}$ (क्यों?)
क्या आप अब देख सकते हैं कि $\mathrm{AB}=\mathrm{CD}$ ?
9.2 केंद्र से जीवा पर लंब
क्रियाकलाप: ट्रेसिंग पेपर पर एक वृत्त खींचें। मान लें कि इसका केंद्र $\mathrm{O}$ है। एक जीवा AB खींचें। पेपर को $\mathrm{O}$ से होकर जाने वाली एक रेखा के साथ इस प्रकार मोड़ें कि जीवा का एक भाग दूसरे पर आ जाए। मान लें कि क्रीज जीवा AB को बिंदु $\mathrm{M}$ पर काटती है। तब, $\angle \mathrm{OMA}=\angle \mathrm{OMB}=90^{\circ}$ या $\mathrm{OM}$ जीवा AB पर लंब है। क्या बिंदु B, A के साथ मेल खाता है (देखें चित्र 9.6)?
हाँ, यह मेल खाएगा। इसलिए MA=MB।
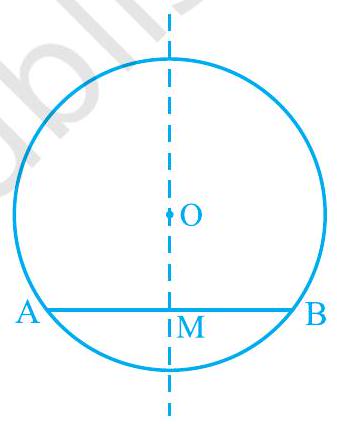
चित्र 9.6
$\mathrm{OA}$ और $\mathrm{OB}$ को मिलाकर स्वयं प्रमाण दें और समकोण त्रिभुजों OMA और OMB को सर्वांगसम सिद्ध करें। यह उदाहरण निम्नलिखित परिणाम का एक विशेष उदाहरण है:
प्रमेय 9.3 : वृत्त के केंद्र से जीवा पर डाला गया लंब जीवा को समद्विभाजित करता है।
इस प्रमेय का विलोम क्या है? यह लिखने के लिए पहले स्पष्ट कर लें कि प्रमेय 9.3 में क्या मान लिया गया है और क्या सिद्ध किया गया है। दिया गया है कि वृत्त के केंद्र से जीवा पर एक लंब डाला गया है और सिद्ध करना है कि वह जीवा को समद्विभाजित करता है। इस प्रकार विलोम में, कल्पना यह है कि ‘यदि केंद्र से जाने वाली एक रेखा वृत्त की जीवा को समद्विभाजित करती है’ और सिद्ध करना है कि ‘रेखा जीवा पर लंब है’। इसलिए विलोम है:
प्रमेय 9.4 : वृत्त के केंद्र से होकर जीवा को समद्विभाजित करने के लिए खींची गई रेखा जीवा पर लंब होती है।
क्या यह सत्य है? कुछ मामलों के लिए आजमाकर देखें। आप देखेंगे कि यह इन मामलों के लिए सत्य है। यह देखने के लिए कि क्या यह सामान्य रूप से सत्य है, निम्न अभ्यास करें। हम चरण लिखेंगे और आप कारण बताइए।
मान लीजिए (\mathrm{AB}) केंद्र (\mathrm{O}) वाले वृत्त की एक जीवा है और (\mathrm{O}) को (\mathrm{AB}) के मध्य-बिंदु (\mathrm{M}) से मिलाया गया है। आपको सिद्ध करना है कि (\mathrm{OM} \perp \mathrm{AB}) है। (\mathrm{OA}) और (\mathrm{OB}) को मिलाइए (देखिए आकृति 9.7)। त्रिभुजों OAM और OBM में,
$$ \begin{aligned} \mathrm{OA} & =\mathrm{OB}\quad \text{(क्यों ?)}\\ \mathrm{AM} & =\mathrm{BM}\quad \text{(क्यों ?)} \\ \mathrm{OM} & =\mathrm{OM}\quad \text{(उभयनिष्ठ)} \end{aligned} $$
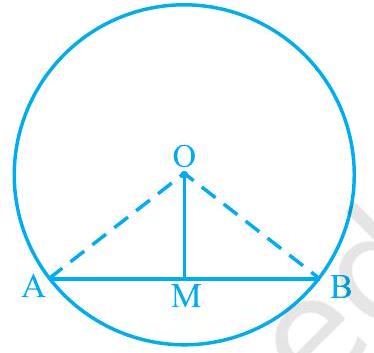
आकृति 9.7
इसलिए, $\triangle \mathrm{OAM} \cong \triangle \mathrm{OBM}\quad \text{(कैसे ?)}$
इससे प्राप्त होता है $\angle \mathrm{OMA}=\angle \mathrm{OMB}=90^{\circ} \quad$ (क्यों?)
9.3 समान जीवाएँ और उनकी केंद्र से दूरी
मान लीजिए $\mathrm{AB}$ एक रेखा है और $\mathrm{P}$ एक बिंदु है। चूँकि एक रेखा पर अनगिनत बिंदु होते हैं, यदि आप इन बिंदुओं को $\mathrm{P}$ से मिलाते हैं, तो आपको अनगिनत रेखाखंड $\mathrm{PL_1}, \mathrm{PL_2}, \mathrm{PM}, \mathrm{PL_3}, \mathrm{PL_4}$, आदि प्राप्त होंगे। इनमें से कौन-सा रेखाखंड AB की P से दूरी है? आप थोड़ा सोचें और उत्तर प्राप्त करें। इन सभी रेखाखंडों में से, रेखा AB पर बिंदु P से डाला गया लंब, अर्थात् आकृति 9.8 में $\mathrm{PM}$, सबसे छोटा होगा। गणित में हम इस न्यूनतम लंबाई $P M$ को $AB$ की $P$ से दूरी मानते हैं। तो आप कह सकते हैं कि:
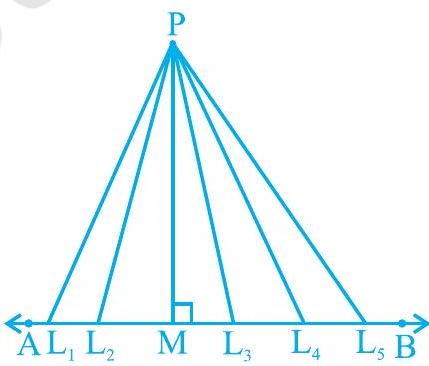
आकृति 9.8
एक बिंदु से किसी रेखा पर डाले गए लंब की लंबाई उस रेखा की उस बिंदु से दूरी होती है।
ध्यान दें कि यदि बिंदु रेखा पर स्थित है, तो रेखा की उस बिंदु से दूरी शून्य होती है।
एक वृत्त में अनंत जीवाएँ हो सकती हैं। आप एक वृत्त की जीवाएँ खींचकर देख सकते हैं कि बड़ी जीवा छोटी जीवा की तुलना में केंद्र के निकट होती है। आप एक वृत्त की विभिन्न लंबाइयों की कई जीवाएँ खींचकर और उनकी केंद्र से दूरी मापकर यह प्रेक्षण कर सकते हैं। व्यास, जो सबसे बड़ी जीवा है, की केंद्र से दूरी क्या है? चूँकि केंद्र उस पर स्थित होता है, इसलिए दूरी शून्य है। क्या आपको लगता है कि जीवाओं की लंबाई और उनकी केंद्र से दूरी के बीच कोई संबंध है? आइए देखें कि ऐसा है या नहीं।
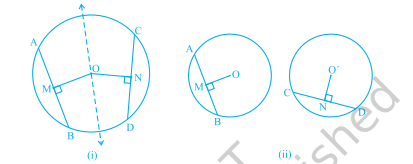
आकृति 9.9
गतिविधि : ट्रेसिंग पेपर पर किसी भी त्रिज्या का एक वृत्त खींचें। उसमें दो बराबर जीवाएँ $\mathrm{AB}$ और $\mathrm{CD}$ खींचें और केंद्र O से उन पर लंब $\mathrm{OM}$ और $\mathrm{ON}$ भी खींचें। आकृति को इस प्रकार मोड़ें कि D, B पर आ जाए और C, A पर आ जाए [देखें चित्र 9.9 (i)]। आप देख सकते हैं कि $\mathrm{O}$ क्रीज़ पर स्थित है और $\mathrm{N}$, $\mathrm{M}$ पर आ जाता है। इसलिए, $\mathrm{OM}=\mathrm{ON}$। गतिविधि को दोहराएँ केंद्रों $\mathrm{O}$ और $\mathrm{O}^{\prime}$ वाले सर्वांगसम वृत्त खींचकर और प्रत्येक पर बराबर जीवाएँ $A B$ और $C D$ लेकर। उन पर लंब $O M$ और $O^{\prime} N$ खींचें [देखें चित्र 9.9(ii)]। एक वृत्ताकार डिस्क को काटें और दूसरे पर इस प्रकार रखें कि $A B$, $\mathrm{CD}$ के संपाती हो जाएँ। तब आप पाएँगे कि $\mathrm{O}$, $\mathrm{O}^{\prime}$ के संपाती हो जाता है और $\mathrm{M}$, $\mathrm{N}$ के संपाती हो जाता है। इस प्रकार आपने निम्न को सत्यापित किया:
प्रमेय 9.5 : एक वृत्त (या सर्वांगसम वृत्तों) की बराबर जीवाएँ केंद्र (या केंद्रों) से समदूरस्थ होती हैं।
अब यह देखा जाएगा कि क्या इस प्रमेय का विलोम सत्य है या नहीं। इसके लिए, केंद्र O से एक वृत्त खींचिए। केंद्र O से, दो रेखाखंड OL और OM समान लंबाई के और वृत्त के अंदर स्थित खींचिए [देखिए आकृति 9.10(i)]। फिर वृत्त की जीवाएँ PQ और RS खींचिए जो क्रमशः OL और OM पर लंबवत हों [देखिए आकृति 9.10(ii)]। PQ और RS की लंबाइयाँ मापिए। क्या ये भिन्न हैं? नहीं, दोनों समान हैं। इस क्रिया को और अधिक समान रेखाखंडों के लिए दोहराइए और उन पर लंबवत जीवाएँ खींचिए। यह प्रमेय 9.5 के विलोम को सत्यापित करता है जो इस प्रकार कहा गया है:
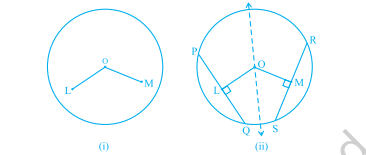
आकृति 9.10
प्रमेय 9.6 : वृत्त के केंद्र से समान दूरी पर स्थित जीवाएँ लंबाई में समान होती हैं। अब हम उपरोक्त परिणामों के उपयोग को दर्शाने के लिए एक उदाहरण लेते हैं:
उदाहरण 1 : यदि किसी वृत्त की दो प्रतिच्छेदी जीवाएँ उस व्यास के साथ समान कोण बनाती हैं जो उनके प्रतिच्छेद बिंदु से गुजरता है, तो सिद्ध कीजिए कि जीवाएँ समान हैं।
हल : दिया गया है कि $\mathrm{AB}$ और $\mathrm{CD}$ किसी वृत्त की दो जीवाएँ हैं, जिसका केंद्र $\mathrm{O}$ है और ये बिंदु $\mathrm{E}$ पर प्रतिच्छेद करती हैं। $\mathrm{PQ}$ एक व्यास है जो $\mathrm{E}$ से गुजरता है, इस प्रकार कि $\angle \mathrm{AEQ}=\angle \mathrm{DEQ}$ (देखिए आकृति 9.11)। आपको सिद्ध करना है कि $\mathrm{AB}=\mathrm{CD}$। जीवाओं $\mathrm{AB}$ और $\mathrm{CD}$ पर लंबवत लंब OL और OM खींचिए। अब
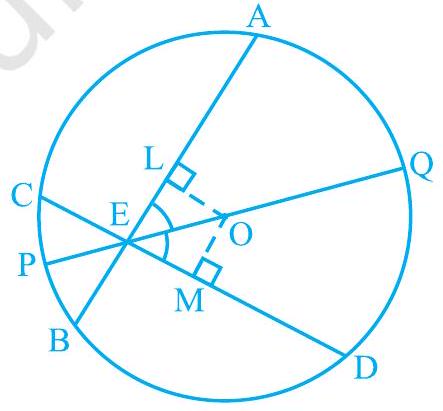
चित्र 9.11
$$ \begin{aligned} \angle \mathrm{LOE}= & 180^{\circ}-90^{\circ}-\angle \mathrm{LEO}=90^{\circ}-\angle \mathrm{LEO} \\ & \quad(\text{ त्रिभुज का कोण योग गुणधर्म }) \\ = & 90^{\circ}-\angle \mathrm{AEQ}=90^{\circ}-\angle \mathrm{DEQ} \\ = & 90^{\circ}-\angle \mathrm{MEO}=\angle \mathrm{MOE} \end{aligned} $$
त्रिभुज OLE और OME में,
$$ \begin{aligned} \angle \mathrm{LEO} & =\angle \mathrm{MEO}\quad \quad \text{(क्यों ?)} \\ \angle \mathrm{LOE} & =\angle \mathrm{MOE}\quad \quad \text{(ऊपर सिद्ध किया गया)} \\ \mathrm{EO} & =\mathrm{EO}\quad \quad \text{(उभयनिष्ठ)} \\ \text{इसलिए},\quad\Delta \mathrm{OLE} & \cong \Delta \mathrm{OME}\quad \quad \text{(क्यों ?)} \\ \text{इससे प्राप्त होता है}\quad\mathrm{OL} & =\mathrm{OM}\quad \quad \text{(CPCT)} \\ \text{ इसलिए, }\quad\mathrm{AB} & =\mathrm{CD}\quad \quad \text{(क्यों?)} \end{aligned} $$
9.4 वृत्त के चाप द्वारा अंतरित कोण
आपने देखा है कि एक वृत्त के व्यास के अतिरिक्त किसी जीवा के अंतिम बिंदु उसे दो चापों में विभाजित करते हैं — एक बड़ा और एक छोटा। यदि आप दो समान जीवाएँ लें, तो आप इन चापों के आकार के बारे में क्या कह सकते हैं? क्या पहली जीवा द्वारा बना हुआ चाप दूसरी जीवा द्वारा बने संगत चाप के बराबर है? वास्तव में, वे केवल लंबाई में समान नहीं हैं। वे सर्वांगसम (congruent) हैं इस अर्थ में कि यदि एक चाप को दूसरे चाप पर, मोड़े या तोड़े बिना रखा जाए, तो वह पूरी तरह से दूसरे के ऊपर आ जाता है।
आप इस तथ्य की पुष्टि इस प्रकार कर सकते हैं: जीवा $\mathrm{CD}$ के संगत चाप को वृत्त से $\mathrm{CD}$ के साथ-साथ काटकर उस चाप पर रखें जो समान जीवा AB द्वारा बनाई गई है। आप पाएंगे कि चाप CD पूरी तरह से चाप AB के ऊपर आ जाता है (देखें आकृति 9.13)। इससे यह सिद्ध होता है कि समान जीवाएँ सर्वांगसम चाप बनाती हैं और इसके विपरीत, सर्वांगसम चाप समान जीवाएँ बनाती हैं। आप इसे इस प्रकार कह सकते हैं:
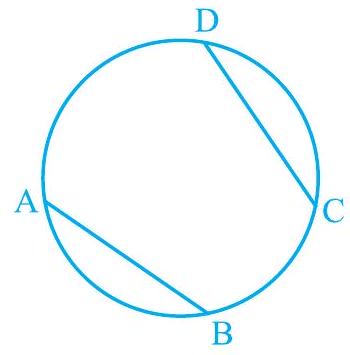
आकृति 9.13
यदि किसी वृत्त की दो जीवाएँ समान हैं, तो उनके संगत चाप सर्वांगसम होते हैं और इसके विपरीत, यदि दो चाप सर्वांगसम हैं, तो उनकी संगत जीवाएँ समान होती हैं।
साथ ही, किसी चाप द्वारा केंद्र पर बनाया गया कोण उस संगत जीवा द्वारा केंद्र पर बनाए गए कोण के रूप में परिभाषित किया जाता है, इस अर्थ में कि लघु चाप कोण बनाता है और दीर्घ चाप प्रतिबिंबित कोण बनाता है। इसलिए, चित्र 9.14 में, लघु चाप $\mathrm{PQ}$ द्वारा $\mathrm{O}$ पर बनाया गया कोण $\angle \mathrm{POQ}$ है और दीर्घ चाप $\mathrm{PQ}$ द्वारा $\mathrm{O}$ पर बनाया गया कोण प्रतिबिंबित कोण POQ है।
उपरोक्त गुणधर्म और प्रमेय 9.1 के दृष्टिकोण से, निम्नलिखित परिणाम सत्य है:
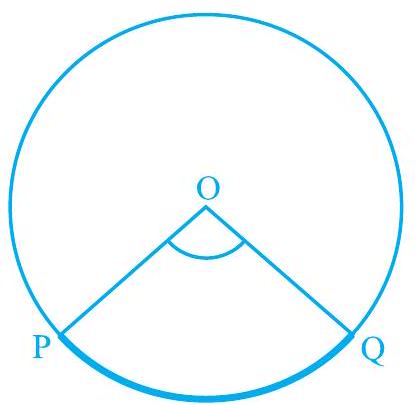
चित्र 9.14
एक वृत्त के सर्वांगसम चाप (या समान चाप) केंद्र पर समान कोण बनाते हैं।
इसलिए, एक वृत्त की जीवा द्वारा उसके केंद्र पर बनाया गया कोण, संगत (लघु) चाप द्वारा केंद्र पर बनाए गए कोण के बराबर होता है। निम्नलिखित प्रमेय एक चाप द्वारा केंद्र और वृत्त पर किसी बिंदु पर बनाए गए कोणों के बीच संबंध देती है।
प्रमेय 9.7 : एक चाप द्वारा केंद्र पर बनाया गया कोण, वृत्त के शेष भाग पर किसी बिंदु पर बनाए गए कोण का दुगना होता है।
प्रमाण : दिया गया है कि एक वृत्त के चाप PQ केंद्र $\mathrm{O}$ पर कोण POQ और वृत्त के शेष भाग पर बिंदु $A$ पर कोण PAQ बनाता है। हमें यह सिद्ध करना है कि $\angle \mathrm{POQ}=2 \angle \mathrm{PAQ}$।
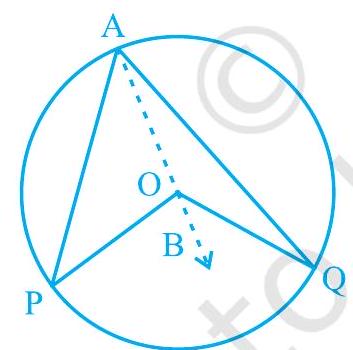
(i)
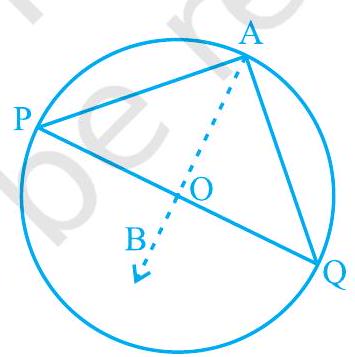
(ii)
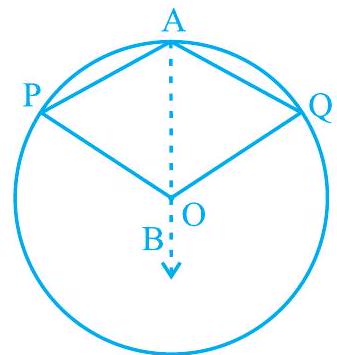
(iii)
Fig. 9.15
Fig. 9.15 में दिए गए तीन भिन्न-भिन्न स्थितियों पर विचार करें। (i) में, चाप PQ लघु है; (ii) में, चाप PQ अर्धवृत्त है और (iii) में, चाप PQ दीर्घ है।
आइए $\mathrm{AO}$ को मिलाकर उसे बिंदु $\mathrm{B}$ तक बढ़ाते हैं।
सभी स्थितियों में,
$$ \angle \mathrm{BOQ}=\angle \mathrm{OAQ}+\angle \mathrm{AQO} $$
क्योंकि त्रिभुज का बाह्य कोण उसके दो आंतरिक विपरीत कोणों के योग के बराबर होता है।
इसके अतिरिक्त $\triangle \mathrm{OAQ}$ में,
$\quad \quad \quad \mathrm{OA}=\mathrm{OQ}\quad \text{(एक वृत्त की त्रिज्याएँ)}$
इसलिए, $\quad \angle \mathrm{OAQ}=\angle \mathrm{OQA} \quad \text{(प्रमेय 7.5)}$
इससे प्राप्त होता है $\quad \angle \mathrm{BOQ}=2 \angle \mathrm{OAQ} \quad (1)$
इसी प्रकार, $ \quad \angle \mathrm{BOP}=2 \angle \mathrm{OAP} \quad (2)$
(1) और (2) से, $\quad \angle \mathrm{BOP}+\angle \mathrm{BOQ}=2(\angle \mathrm{OAP}+\angle \mathrm{OAQ})$
यह $\quad \angle \mathrm{POQ}=2 \angle \mathrm{PAQ}\quad (3)$ के समान है
स्थिति (iii) के लिए, जहाँ $\mathrm{PQ}$ बड़ा चाप है, (3) को इससे बदल दिया जाता है
$\text { उल्लम्ब कोण } \mathrm{POQ}=2 \angle \mathrm{PAQ}$
टिप्पणी : मान लीजिए हम बिंदुओं $\mathrm{P}$ और $\mathrm{Q}$ को मिलाते हैं और उपरोक्त आकृतियों में एक जीवा PQ बनाते हैं। तब $\angle \mathrm{PAQ}$ को खंड PAQP में बना कोण भी कहा जाता है।
प्रमेय 9.7 में, A वृत्त के शेष भाग पर कोई भी बिंदु हो सकता है। इसलिए यदि आप वृत्त के शेष भाग पर कोई अन्य बिंदु $\mathrm{C}$ लेते हैं (देखें आकृति 9.16), तो आपके पास
$\quad \quad \quad \angle \mathrm{POQ}=2 \angle \mathrm{PCQ}=2 \angle \mathrm{PAQ}$
इसलिए, $\quad \angle \mathrm{PCQ}=2 \angle \mathrm{PAQ}$।
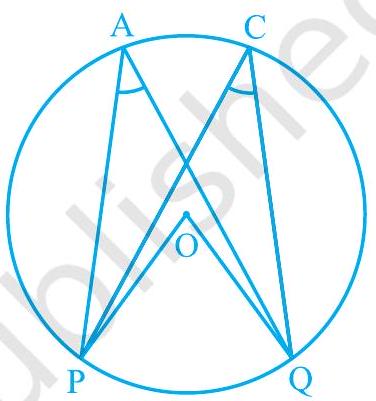
आकृति 9.16
इससे निम्नलिखित सिद्ध होता है:
प्रमेय 9.8 : वृत्त के समान खंड में बने कोण समान होते हैं।
आइए एक बार फिर से प्रमेय 10.8 की स्थिति (ii) पर अलग से चर्चा करें। यहाँ $\angle \mathrm{PAQ}$ एक खंड में बना कोण है, जो अर्धवृत्त है। साथ ही, $\angle \mathrm{PAQ}=\frac{1}{2} \angle \mathrm{POQ}=\frac{1}{2} \times 180^{\circ}=90^{\circ}$। यदि आप अर्धवृत्त पर कोई अन्य बिंदु $\mathrm{C}$ लेते हैं, तो आपको फिर से यही मिलता है
$\angle \mathrm{PCQ}=90^{\circ}$
इसलिए, आप वृत्त का एक अन्य गुणधर्म पाते हैं:
अर्धवृत्त में कोण समकोण होता है।
प्रमेय 9.8 का प्रतिकथन भी सत्य है। इसे इस प्रकार कहा जा सकता है:
प्रमेय 9.9 : यदि दो बिंदुओं को मिलाने वाली एक रेखाखंड उस रेखा के एक ही ओर स्थित दो अन्य बिंदुओं पर समान कोण अंतरित करती है, तो चारों बिंदु एक वृत्त पर स्थित होते हैं (अर्थात् वे संवृत्त हैं)।
आप इस परिणाम की सत्यता इस प्रकार देख सकते हैं:
चित्र 9.17 में, $\mathrm{AB}$ एक रेखाखंड है, जो दो बिंदुओं $\mathrm{C}$ और $\mathrm{D}$ पर समान कोण अंतरित करता है। अर्थात्
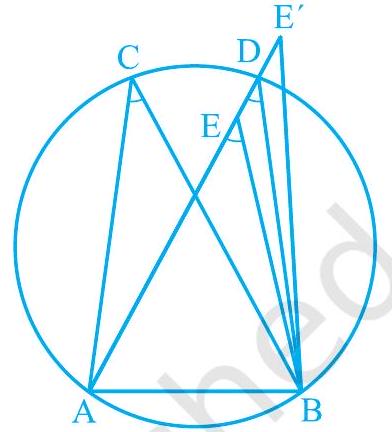
चित्र 9.17
$$ \angle \mathrm{ACB}=\angle \mathrm{ADB} $$
यह दिखाने के लिए कि बिंदु $\mathrm{A}, \mathrm{B}, \mathrm{C}$ और $\mathrm{D}$ एक वृत्त पर स्थित हैं, आइए बिंदुओं A, C और B से होकर जाने वाला एक वृत्त खींचें। मान लीजिए यह बिंदु $\mathrm{D}$ से नहीं गुजरता। तब यह $\mathrm{AD}$ (या विस्तारित $\mathrm{AD}$) को एक बिंदु, मान लीजिए $\mathrm{E}$ (या $\mathrm{E}^{\prime}$) पर काटेगा।
यदि बिंदु $\mathrm{A}, \mathrm{C}, \mathrm{E}$ और $\mathrm{B}$ एक वृत्त पर स्थित हैं,
$$ \angle \mathrm{ACB}=\angle \mathrm{AEB} \quad \text{(क्यों?)} $$
परंतु दिया गया है कि $\quad \angle \mathrm{ACB}=\angle \mathrm{ADB}$।
इसलिए, $\quad \quad \angle \mathrm{AEB}=\angle \mathrm{ADB} .$
यह संभव नहीं है जब तक $\mathrm{E}$, $\mathrm{D}$ के संपाती न हो। (क्यों?)
इसी प्रकार, E’ को भी D के संपाती होना चाहिए।
9.5 चक्रीय चतुर्भुज
एक चतुर्भुज $\mathrm{ABCD}$ को चक्रीय कहा जाता है यदि इसके सभी चार शीर्ष एक वृत्त पर स्थित हों (देखें चित्र 9.18)। आप ऐसे चतुर्भुजों में एक विचित्र गुणधर्म पाएंगे। विभिन्न भुजाओं वाले कई चक्रीय चतुर्भुज बनाएं और प्रत्येक को ABCD नाम दें। (यह विभिन्न त्रिज्याओं के कई वृत्त बनाकर और प्रत्येक पर चार बिंदु लेकर किया जा सकता है।) विपरीत कोणों को मापिए और अपने प्रेक्षण निम्न सारणी में लिखिए।
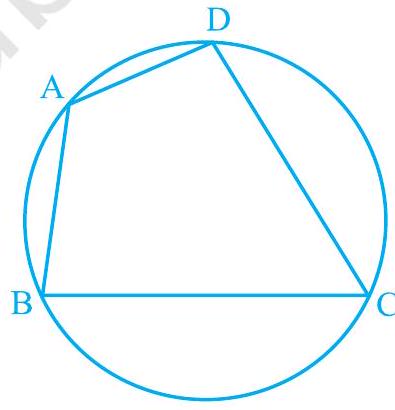
चित्र 9.18
| चतुर्भुज का क्रम सं. | $\angle \mathrm{A}$ | $\angle \mathrm{B}$ | $\angle \mathrm{C}$ | $\angle \mathrm{D}$ | $\angle \mathrm{A}+\angle \mathrm{C}$ | $\angle \mathrm{B}+\angle \mathrm{D}$ |
|---|---|---|---|---|---|---|
| 1. | ||||||
| 2. | ||||||
| 3. | ||||||
| 4. | ||||||
| 5. | ||||||
| 6. |
आप सारणी से क्या निष्कर्ष निकालते हैं?
आप पाते हैं कि $\angle \mathrm{A}+\angle \mathrm{C}=180^{\circ}$ और $\angle \mathrm{B}+\angle \mathrm{D}=180^{\circ}$ है, मापन की त्रुटि को नजरअंदाज करते हुए। यह निम्नलिखित को सत्यापित करता है:
प्रमेय 9.10 : एक चक्रीय चतुर्भुज के विपरीत कोणों के किसी भी युग्म का योग $180^{\circ}$ होता है।
वास्तव में, इस प्रमेय का विलोम, जो नीचे दिया गया है, भी सत्य है।
प्रमेय 9.11 : यदि किसी चतुर्भुज के विपरीत कोणों के एक युग्म का योग $180^{\circ}$ है, तो चतुर्भुज चक्रीय है।
आप इस प्रमेय की सत्यता को प्रमेय 9.9 के लिए अपनाई गई विधि के समान विधि का अनुसरण करके देख सकते हैं।
उदाहरण 2 : चित्र 9.19 में, $\mathrm{AB}$ वृत्त का व्यास है, $\mathrm{CD}$ एक जीवा है जो वृत्त की त्रिज्या के बराबर है। $\mathrm{AC}$ और $\mathrm{BD}$ को बढ़ाने पर वे बिंदु $\mathrm{E}$ पर प्रतिच्छेद करते हैं। सिद्ध कीजिए कि $\angle \mathrm{AEB}=60^{\circ}$ है।
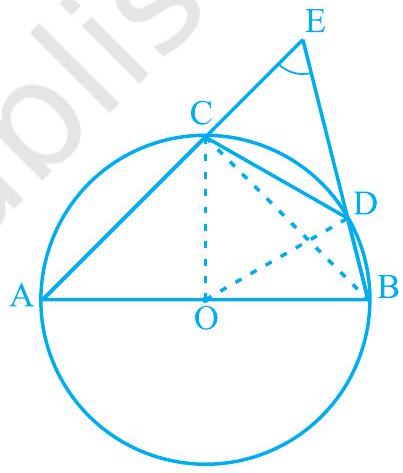
चित्र 9.19
हल : OC, OD और BC को मिलाइए।
त्रिभुज ODC समबाहु है $\quad$ (क्यों?)
इसलिए, $\angle \mathrm{COD}=60^{\circ}$
अब, $\quad \angle \mathrm{CBD}=\frac{1}{2} \angle \mathrm{COD} \quad$ (प्रमेय 9.7)
इससे प्राप्त होता है $\quad \angle \mathrm{CBD}=30^{\circ}$
पुनः, $\quad \angle \mathrm{ACB}=90^{\circ}\quad $(क्यों?)
इसलिए, $\quad \angle \mathrm{BCE}=180^{\circ}-\angle \mathrm{ACB}=90^{\circ}$
जिससे प्राप्त होता है $\angle \mathrm{CEB}=90^{\circ}-30^{\circ}=60^{\circ}$, अर्थात् $\angle \mathrm{AEB}=60^{\circ}$
उदाहरण 3 : आकृति 9.20 में, ABCD एक चक्रीय चतुर्भुज है जिसमें $\mathrm{AC}$ और $\mathrm{BD}$ इसके विकर्ण हैं। यदि $\angle \mathrm{DBC}=55^{\circ}$ और $\angle \mathrm{BAC}=45^{\circ}$ है, तो $\angle \mathrm{BCD}$ ज्ञात कीजिए।
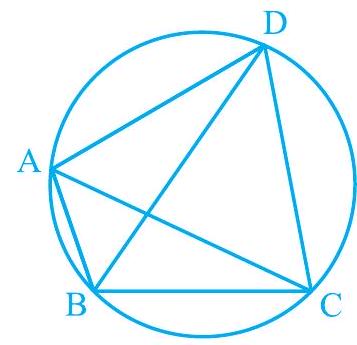
आकृति 9.20
हल : $\quad \angle \mathrm{CAD}=\angle \mathrm{DBC}=55^{\circ}$ (एक ही खंड में स्थित कोण)
$$ \begin{aligned} \text{इसलिए,}\quad \angle \mathrm{DAB} & =\angle \mathrm{CAD}+\angle \mathrm{BAC} \ & =55^{\circ}+45^{\circ}=100^{\circ} \end{aligned} $$
लेकिन $\quad \angle \mathrm{DAB}+\angle \mathrm{BCD}=180^{\circ}$
(चक्रीय चतुर्भुज के सम्मुख कोण)
इसलिए,$\quad \angle \mathrm{BCD}=180^{\circ}-100^{\circ}=80^{\circ}$
उदाहरण 4 : दो वृत्त दो बिंदुओं A और $\mathrm{B}$ पर प्रतिच्छेद करते हैं। $\mathrm{AD}$ और $\mathrm{AC}$ दोनों वृत्तों के व्यास हैं (देखिए आकृति 9.21)। सिद्ध कीजिए कि B रेखाखंड DC पर स्थित है।
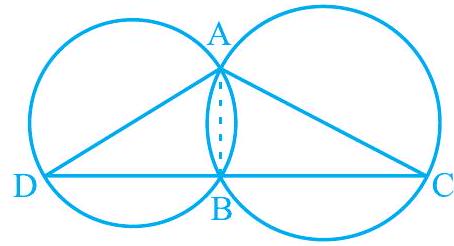
आकृति 9.21
हल : AB को मिलाइए।
$$ \begin{aligned} & \angle \mathrm{ABD}=90^{\circ} \quad(\text{अर्धवृत्त में कोण}) \ & \angle \mathrm{ABC}=90^{\circ} \quad(\text{अर्धवृत्त में कोण}) \end{aligned} $$
इसलिए, $\quad \angle \mathrm{ABD}+\angle \mathrm{ABC}=90^{\circ}+90^{\circ}=180^{\circ}$
अतः, $\mathrm{DBC}$ एक रेखा है। अर्थात् $\mathrm{B}$ बिन्दु रेखाखण्ड $\mathrm{DC}$ पर स्थित है।
उदाहरण 5 : सिद्ध कीजिए कि किसी भी चतुर्भुज के आंतरिक कोण समद्विभाजकों द्वारा बनाया गया चतुर्भुज (यदि संभव हो) चक्रीय होता है।
हल : आकृति 9.22 में, ABCD एक चतुर्भुज है जिसमें आंतरिक कोणों A, B, C और D के कोण समद्विभाजक $\mathrm{AH}, \mathrm{BF}, \mathrm{CF}$ और $\mathrm{DH}$ क्रमशः एक चतुर्भुज $\mathrm{EFGH}$ बनाते हैं।
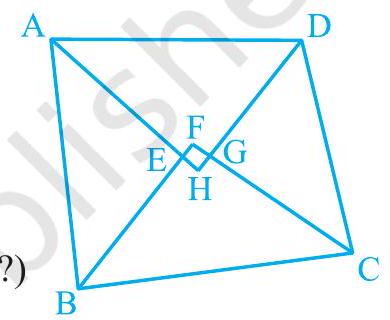
आकृति 9.22
$$ \begin{aligned} \text{अब,}\quad \angle \mathrm{FEH}=\angle \mathrm{AEB} & =180^{\circ}-\angle \mathrm{EAB}-\angle \mathrm{EBA}(\text { क्यों? }) \ & =180^{\circ}-\frac{1}{2}(\angle \mathrm{A}+\angle \mathrm{B}) \end{aligned} $$
तथा $\angle \mathrm{FGH}=\angle \mathrm{CGD}=180^{\circ}-\angle \mathrm{GCD}-\angle \mathrm{GDC} \quad$ (क्यों?) $$ =180^{\circ}-\frac{1}{2}(\angle \mathrm{C}+\angle \mathrm{D}) $$
इसलिए, $\angle \mathrm{FEH}+\angle \mathrm{FGH}=180^{\circ}-\frac{1}{2}(\angle \mathrm{A}+\angle \mathrm{B})+180^{\circ}-\frac{1}{2}(\angle \mathrm{C}+\angle \mathrm{D})$
$$ \begin{aligned} & =360^{\circ}-\frac{1}{2}(\angle \mathrm{A}+\angle \mathrm{B}+\angle \mathrm{C}+\angle \mathrm{D})=360^{\circ}-\frac{1}{2} \times 360^{\circ} \\ & =360^{\circ}-180^{\circ}=180^{\circ} \end{aligned} $$
इसलिए, प्रमेय 9.11 द्वारा, चतुर्भुज EFGH चक्रीय है।
9.6 सारांश
इस अध्याय में, आपने निम्नलिखित बिंदुओं का अध्ययन किया है:
1. एक वृत्त उस समतल में स्थित सभी बिंदुओं का समूह है जो समतल में एक निश्चित बिंदु से समान दूरी पर होते हैं।
2. एक वृत्त (या सर्वांगसम वृत्तों) की समान जीवाएँ केंद्र पर समान कोण अंतरित करती हैं।
3. यदि एक वृत्त (या सर्वांगसम वृत्तों) की दो जीवाओं द्वारा केंद्र (संगत केंद्रों) पर अंतरित कोण समान हों, तो जीवाएँ समान होती हैं।
4. वृत्त के केंद्र से जीवा पर डाला गया लंब जीवा को समद्विभाजित करता है।
5. वृत्त के केंद्र से होकर जीवा के समद्विभाजक के रूप में खींची गई रेखा जीवा पर लंब होती है।
6. एक वृत्त (या सर्वांगसम वृत्तों) की समान जीवाएँ केंद्र (या संगत केंद्रों) से समान दूरी पर होती हैं।
7. जो जीवाएँ वृत्त (या सर्वांगसम वृत्तों) के केंद्र (या संगत केंद्रों) से समान दूरी पर हों, वे समान होती हैं।
8. यदि एक वृत्त के दो चाप सर्वांगसम हों, तो उनकी संगत जीवाएँ समान होती हैं और इसका विलोम भी सत्य है—यदि एक वृत्त की दो जीवाएँ समान हों, तो उनके संगत चाप (लघु, दीर्घ) सर्वांगसम होते हैं।
9. एक वृत्त के सर्वांगसम चाप केंद्र पर समान कोण अंतरित करते हैं।
10. किसी चाप द्वारा केंद्र पर अंतरित कोण, वृत्त के शेष भाग पर स्थित किसी बिंदु पर अंतरित कोण की तुलना में दोगुना होता है।
11. एक वृत्त के समान खंड में स्थित कोण समान होते हैं।
12. अर्धवृत्त में स्थित कोण समकोण होता है।
13. यदि दो बिंदुओं को मिलाने वाली रेखाखंड उस रेखा के एक ही ओर स्थित दो अन्य बिंदुओं पर समान कोण अंतरित करती है, जिसमें वह रेखाखंड स्थित है, तो चारों बिंदु एक वृत्त पर स्थित होते हैं।
14. एक चक्रीय चतुर्भुज के किसी भी युग्म के सम्मुख कोणों का योग $180^{\circ}$ होता है।
15. यदि किसी चतुर्भुज के सम्मुख कोणों के किसी युग्म का योग $180^{\circ}$ हो, तो वह चतुर्भुज चक्रीय होता है।











