8.1 समांतर चतुर्भुज के गुण

आप पहले ही कक्षा VIII में चतुर्भुजों और उनके प्रकारों का अध्ययन कर चुके हैं। एक चतुर्भुज में चार भुजाएँ, चार कोण और चार शीर्ष होते हैं। समांतर चतुर्भुज एक ऐसा चतुर्भुज है जिसकी दोनों विपरीत भुजाओं के युग्म समांतर होते हैं। आइए एक गतिविधि करें।

एक कागज की शीट से एक समांतर चतुर्भुज काटें और उसे एक विकर्ण के साथ काटें (देखें Fig. 8.1)। आपको दो त्रिभुज प्राप्त होते हैं। आप इन त्रिभुजों के बारे में क्या कह सकते हैं?

एक त्रिभुज को दूसरे के ऊपर रखें। आवश्यकता होने पर एक को घुमाएँ। आप क्या देखते हैं?

देखें कि दोनों त्रिभुज एक-दूसरे के सर्वांगसम हैं।

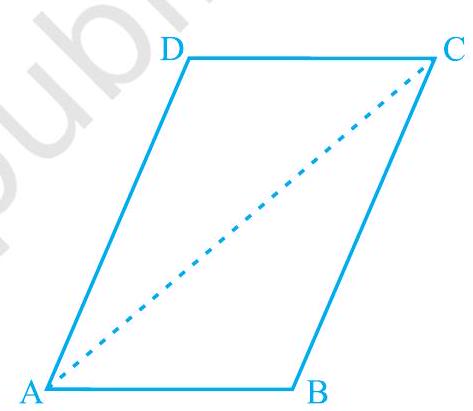
Fig. 8.1

इस गतिविधि को कुछ और समांतर चतुर्भुजों के साथ दोहराएँ। हर बार आप देखेंगे कि प्रत्येक विकर्ण समांतर चतुर्भुज को दो सर्वांगसम त्रिभुजों में विभाजित करता है। आइए अब इस परिणाम को सिद्ध करें।

प्रमेय 8.1 : समांतर चतुर्भुज का एक विकर्ण उसे दो सर्वांगसम त्रिभुजों में विभाजित करता है।

प्रमाण : मान लीजिए $A B C D$ एक समांतर चतुर्भुज है और $A C$ एक विकर्ण है (देखें Fig. 8.2)। देखें कि विकर्ण $\mathrm{AC}$ समांतर चतुर्भुज $\mathrm{ABCD}$ को दो त्रिभुजों में विभाजित करता है, अर्थात्, $\triangle \mathrm{ABC}$ और $\triangle \mathrm{CDA}$। हमें यह सिद्ध करना है कि ये त्रिभुज सर्वांगसम हैं।

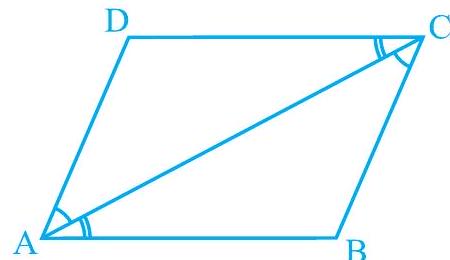
आकृति 8.2

$\triangle \mathrm{ABC}$ और $\triangle \mathrm{CDA}$ में, ध्यान दें कि $\mathrm{BC} || \mathrm{AD}$ और $\mathrm{AC}$ एक अनुप्रस्थ रेखा है।

इसलिए, $\quad \angle \mathrm{BCA}=\angle \mathrm{DAC}$ (एक युग्म of alternate angles)

साथ ही, $\quad\mathrm{AB} | \mathrm{DC}$ और $\mathrm{AC}$ एक अनुप्रस्थ रेखा है।

इसलिए, $\quad \angle \mathrm{BAC}=\angle \mathrm{DCA}$ (एक युग्म of alternate angles)

और $\quad \mathrm{AC}=\mathrm{CA}\quad$(उभयनिष्ठ)

इसलिए, $\quad \Delta \mathrm{ABC} \cong \triangle \mathrm{CDA}\quad$(ASA नियम)

या, विकर्ण $\mathrm{AC}$ समांतर चतुर्भुज $\mathrm{ABCD}$ को दो सर्वांगसम त्रिभुजों $\mathrm{ABC}$ और $\mathrm{CDA}$ में विभाजित करता है।

अब, समांतर चतुर्भुज $A B C D$ की विपरीत भुजाओं को मापिए। आप क्या देखते हैं?

आप पाएंगे कि $\mathrm{AB}=\mathrm{DC}$ और $\mathrm{AD}=\mathrm{BC}$।

यह समांतर चतुर्भुज का एक और गुण है जो नीचे दिया गया है:

प्रमेय 8.2 : एक समांतर चतुर्भुज में, विपरीत भुजाएं बराबर होती हैं।

आप पहले ही सिद्ध कर चुके हैं कि एक विकर्ण समांतर चतुर्भुज को दो सर्वांगसम त्रिभुजों में विभाजित करता है; तो आप संगत भागों, कहिए, संगत भुजाओं के बारे में क्या कह सकते हैं? वे बराबर हैं।

इसलिए, $\mathrm{AB}=\mathrm{DC}$ और $\mathrm{AD}=\mathrm{BC}$

अब इस परिणाम का विलोम क्या है? आप पहले से जानते हैं कि प्रमेय में जो कुछ दिया जाता है, विलोम में उसे सिद्ध करना होता है और जो प्रमेय में सिद्ध किया जाता है, विलोम में वह दिया जाता है। इस प्रकार, प्रमेय 8.2 इस प्रकार कही जा सकती है :

यदि एक चतुर्भुज समांतर चतुर्भुज है, तो इसकी प्रत्येक युग्म-विपरीत भुजाएँ बराबर होती हैं। इसलिए इसका विलोम है :

प्रमेय 8.3 : यदि किसी चतुर्भुज की प्रत्येक युग्म-विपरीत भुजाएँ बराबर हों, तो वह समांतर चतुर्भुज होता है।

क्या आप सोच सकते हैं कि ऐसा क्यों है?

मान लीजिए चतुर्भुज ABCD की भुजाएँ AB और CD बराबर हैं और साथ ही AD = BC (देखिए आकृति 8.3)। विकर्ण AC खींचिए।

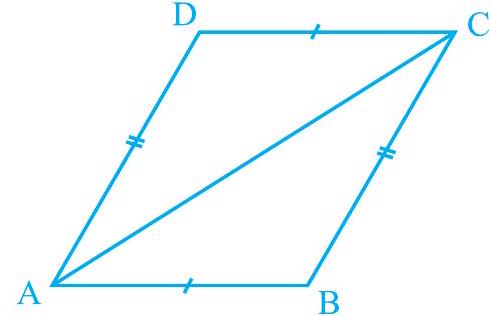
आकृति 8.3

स्पष्ट है कि, $\quad \triangle \mathrm{ABC} \cong \triangle \mathrm{CDA}\quad$(क्यों?)

इसलिए, $\quad \angle \mathrm{BAC}=\angle \mathrm{DCA}$

और $\quad \angle \mathrm{BCA}=\angle \mathrm{DAC}\quad$(क्यों?)

क्या आप अब कह सकते हैं कि ABCD एक समांतर चतुर्भुज है? क्यों?

आपने अभी देखा कि एक समांतर चतुर्भुज में प्रत्येक युग्म-विपरीत भुजाएँ बराबर होती हैं और विलोमतः यदि किसी चतुर्भुज की प्रत्येक युग्म-विपरीत भुजाएँ बराबर हों, तो वह समांतर चतुर्भुज होता है। क्या हम युग्म-विपरीत कोणों के लिए भी यही परिणाम निकाल सकते हैं?

एक समांतर चतुर्भुज खींचिए और उसके कोण मापिए। आप क्या देखते हैं?

प्रत्येक युग्म-विपरीत कोण बराबर होते हैं।

इसे कुछ और समांतर चतुर्भुजों के साथ दोहराएँ। हम नीचे दिए गए एक और परिणाम पर पहुँचते हैं।

प्रमेय 8.4 : एक समांतर चतुर्भुज में, सम्मुख कोण बराबर होते हैं।

अब, क्या इस परिणाम का व्युत्क्रम भी सत्य है? हाँ। चतुर्भुज के कोणों के योग गुणधर्म और एक तिर्यक रेखा द्वारा काटी गई समांतर रेखाओं के परिणामों का उपयोग करके, हम देख सकते हैं कि व्युत्क्रम भी सत्य है। इसलिए, हमारे पास निम्नलिखित प्रमेय है :

प्रमेय 8.5 : यदि किसी चतुर्भुज में, प्रत्येक युग्म सम्मुख कोण बराबर हों, तो वह एक समांतर चतुर्भुज है।

एक समांतर चतुर्भुज का एक और गुणधर्म है। आइए उसे भी अध्ययन करें। एक समांतर चतुर्भुज $\mathrm{ABCD}$ खींचिए और उसके दोनों विकर्णों को बिंदु $\mathrm{O}$ पर प्रतिच्छेद करते हुए खींचिए (देखिए आकृति 8.4)।

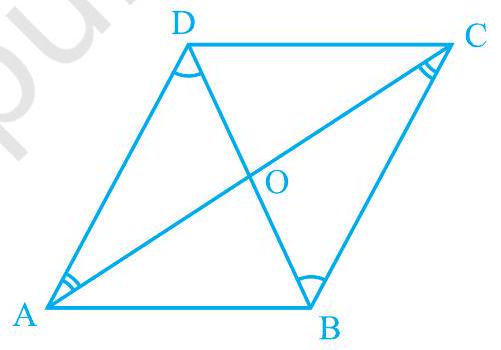
आकृति 8.4

$\mathrm{OA}, \mathrm{OB}, \mathrm{OC}$ और $\mathrm{OD}$ की लंबाइयाँ मापिए।

आप क्या देखते हैं? आप देखेंगे कि

$\mathrm{OA}=\mathrm{OC} \text { और } \mathrm{OB}=\mathrm{OD}$

या, $\mathrm{O}$ दोनों विकर्णों का मध्य-बिंदु है।

इस क्रियाकलाप को कुछ और समांतर चतुर्भुजों के साथ दोहराएँ।

हर बार आप पाएँगे कि $\mathrm{O}$ दोनों विकर्णों का मध्य-बिंदु है।

इसलिए, हमारे पास निम्नलिखित प्रमेय है :

प्रमेय 8.6 : समांतर चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करते हैं।

अब, यदि किसी चतुर्भुज में विकर्ण एक-दूसरे को समद्विभाजित करें तो क्या होगा? क्या वह समांतर चतुर्भुज होगा? यह सच है।

यह परिणाम प्रमेय 8.6 के परिणाम का व्युत्क्रम है। इसे नीचे दिया गया है:

प्रमेय 8.7 : यदि किसी चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करें, तो वह समांतर चतुर्भुज होता है।

आप इस परिणाम को इस प्रकार तर्क दे सकते हैं:

ध्यान दें कि आकृति 8.5 में, यह दिया गया है कि $\mathrm{OA}=\mathrm{OC}$ और $\mathrm{OB}=\mathrm{OD}$।

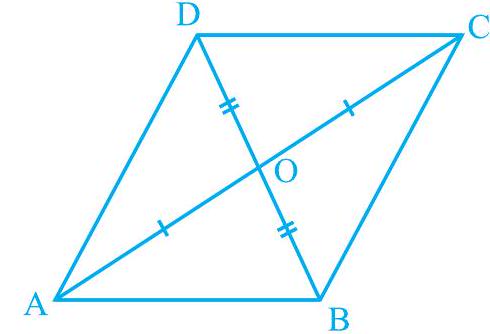
आकृति 8.5

इसलिए,$\quad \triangle \mathrm{AOB} \cong \triangle \mathrm{COD} \quad \text { (क्यों?) }$

इसलिए, $\angle \mathrm{ABO}=\angle \mathrm{CDO}\quad \text {(क्यों?)}$

इससे, हम पाते हैं $\mathrm{AB} || \mathrm{CD}$

इसी प्रकार, $\quad \mathrm{BC} || \mathrm{AD}$

इसलिए $\mathrm{ABCD}$ एक समांतर चतुर्भुज है।

अब हम कुछ उदाहरण लेते हैं।

उदाहरण 1 : दिखाइए कि आयत का प्रत्येक कोण समकोण होता है।

हल : आइए याद करें कि आयत क्या होता है।

आयत एक समांतर चतुर्भुज होता है जिसमें एक कोण समकोण होता है।

मान लीजिए $\mathrm{ABCD}$ एक आयत है जिसमें $\angle \mathrm{A}=90^{\circ}$ है।

हमें दि�ाना है कि $\angle \mathrm{B}=\angle \mathrm{C}=\angle \mathrm{D}=90^{\circ}$

हमारे पास, $A D || B C$ और $A B$ एक अनुप्रस्थ रेखा है (आकृति 8.6 देखें)।

आकृति 8.6

इसलिए, $\angle \mathrm{A}+\angle \mathrm{B}=180^{\circ} \quad$ (एक ही तरफ के आंतरिक कोण)

लेकिन, $\quad \angle \mathrm{A}=90^{\circ}$

इसलिए, $\quad \angle \mathrm{B}=180^{\circ}-\angle \mathrm{A}=180^{\circ}-90^{\circ}=90^{\circ}$

अब, $\quad \angle \mathrm{C}=\angle \mathrm{A}$ और $\angle \mathrm{D}=\angle \mathrm{B}$

(समांतर चतुर्भुज के सम्मुख कोण)

इसलिए,$\quad\angle \mathrm{C}=90^{\circ} \text { और } \angle \mathrm{D}=90^{\circ} \text {. }$

इस प्रकार, आयत का प्रत्येक कोण समकोण होता है।

उदाहरण 2 : दिखाइए कि समचतुर्भुज के विकर्ण एक-दूसरे पर लंब होते हैं।

हल : समचतुर्भुज ABCD पर विचार कीजिए (आकृति 8.7 देखिए)।

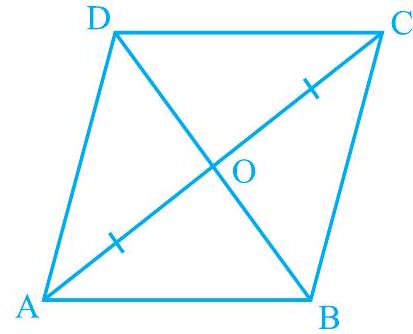
आकृति 8.7

आप जानते हैं कि $\mathrm{AB}=\mathrm{BC}=\mathrm{CD}=\mathrm{DA}$ (क्यों?)

अब, $\triangle \mathrm{AOD}$ और $\triangle \mathrm{COD}$ में,

$\mathrm{OA}=\mathrm{OC}$(समांतर चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करते हैं)

$\mathrm{OD}=\mathrm{OD}\quad$(उभयनिष्ठ)

$\mathrm{AD}=\mathrm{CD}$(दिया है)

इसलिए, $\Delta \mathrm{AOD} \cong \Delta \mathrm{COD}\quad$(SSS सर्वांगसमता नियम)

इससे प्राप्त होता है, $\angle \mathrm{AOD}=\angle \mathrm{COD}\quad$ (CPCT)

लेकिन, $\angle \mathrm{AOD}+\angle \mathrm{COD}=180^{\circ}$ (रैखिक युग्म)

इसलिए, $\quad 2 \angle \mathrm{AOD}=180^{\circ}$

या, $\quad \angle \mathrm{AOD}=90^{\circ}$

इसलिए, एक समचतुर्भुज के विकर्ण एक-दूसरे के लंबवत् होते हैं।

उदाहरण 3 : $\mathrm{ABC}$ एक समद्विबाहु त्रिभुज है जिसमें $\mathrm{AB}=\mathrm{AC}$ है। $\mathrm{AD}$ बाह्य कोण $\mathrm{PAC}$ का समद्विभाजन करता है और $\mathrm{CD} | \mathrm{AB}$ (देखिए आकृति 8.8)। दिखाइए कि

(i) $\angle \mathrm{DAC}=\angle \mathrm{BCA}$ और

(ii) $\mathrm{ABCD}$ एक समांतर चतुर्भुज है।

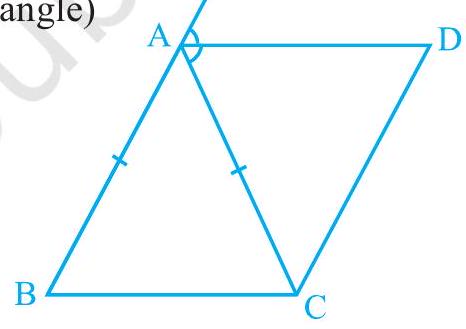
आकृति 8.8

हल : (i) $\triangle \mathrm{ABC}$ समद्विबाहु है जिसमें $\mathrm{AB}=\mathrm{AC}$ (दिया गया है)

इसलिए, $\quad \angle \mathrm{ABC}=\angle \mathrm{ACB} \quad$ (बराबर भुजाओं के सम्मुख कोण)

साथ ही, $\angle \mathrm{PAC}=\angle \mathrm{ABC}+\angle \mathrm{ACB}\quad$(त्रिभुज का बाह्य कोण)

या, $\quad \angle \mathrm{PAC}=2 \angle \mathrm{ACB}\quad$(1)

अब, AD कोण $\mathrm{PAC}$ का समद्विभाजन करता है।

इसलिए, $\quad \angle \mathrm{PAC}=2 \angle \mathrm{DAC}\quad$(2)

इसलिए,

$2 \angle \mathrm{DAC} =2 \angle \mathrm{ACB} \quad[\text { (1) और (2) से }]$
$\text { या, } \quad \angle \mathrm{DAC} =\angle \mathrm{ACB}$

(ii) अब, ये समान कोण एक युग्म के रूप में एकान्तर कोण बनाते हैं जब रेखाखंड $\mathrm{BC}$ और $\mathrm{AD}$ को एक तिर्यक रेखा $\mathrm{AC}$ काटती है।

इसलिए, $\quad \mathrm{BC} || \mathrm{AD}$

साथ ही, $\mathrm{BA} || \mathrm{CD} \quad$ (दिया है)

अब, चतुर्भुज $\mathrm{ABCD}$ की विपरीत भुजाओं के दोनों युग्म समानान्तर हैं।

इसलिए, $A B C D$ एक समान्तर चतुर्भुज है।

उदाहरण 4 : दो समान्तर रेखाएँ $l$ और $m$ एक तिर्यक रेखा $p$ द्वारा प्रतिच्छेदित होती हैं (देखिए आकृति 8.9)। दिखाइए कि आंतरिक कोणों के समद्विभाजकों द्वारा बना चतुर्भुज एक आयत है।

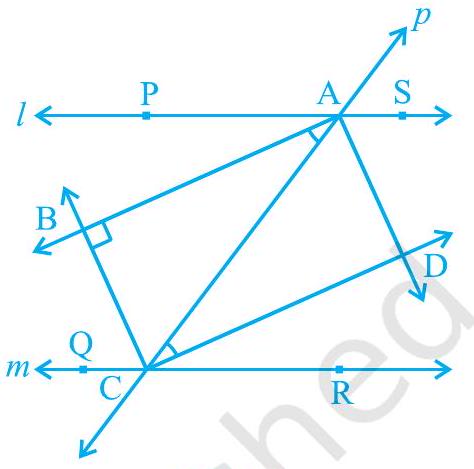
आकृति 8.9

हल : दिया गया है कि PS $|| \mathrm{QR}$ और तिर्यक रेखा $p$ उन्हें बिंदु A और C पर क्रमशः प्रतिच्छेदित करती है।

$\angle \mathrm{PAC}$ और $\angle \mathrm{ACQ}$ के समद्विभाजक बिंदु B पर प्रतिच्छेदित करते हैं और $\angle \mathrm{ACR}$ और $\angle \mathrm{SAC}$ के समद्विभाजक बिंदु D पर प्रतिच्छेदित करते हैं।

हमें दिखाना है कि चतुर्भुज $\mathrm{ABCD}$ एक आयत है।

अब, $\quad \angle \mathrm{PAC}=\angle \mathrm{ACR}$

(एकान्तर कोण क्योंकि $l || m$ और $p$ एक तिर्यक रेखा है)

इसलिए, $\quad \frac{1}{2} \angle \mathrm{PAC}=\frac{1}{2} \angle \mathrm{ACR}$

अर्थात्, $\quad \angle \mathrm{BAC}=\angle \mathrm{ACD}$

ये रेखाओं $\mathrm{AB}$ और $\mathrm{DC}$ के लिए एक युग्म वैकल्पिक कोण बनाते हैं जिनमें $\mathrm{AC}$ एक अनुप्रस्थ रेखा है और वे समान भी हैं।

इसलिए, $\quad\mathrm{AB} || \mathrm{DC}$

इसी प्रकार, $\quad\mathrm{BC} || \mathrm{AD} \quad$ ($\angle \mathrm{ACB}$ और $\angle \mathrm{CAD}$ को ध्यान में रखते हुए)

इसलिए, चतुर्भुज $\mathrm{ABCD}$ एक समांतर चतुर्भुज है।

साथ ही, $\quad\angle \mathrm{PAC}+\angle \mathrm{CAS}=180^{\circ} \quad \text { (रेखीय युग्म) }$

इसलिए, $\quad \frac{1}{2} \angle \mathrm{PAC}+\frac{1}{2} \angle \mathrm{CAS}=\frac{1}{2} \times 180^{\circ}=90^{\circ}$

या, $\quad \angle \mathrm{BAC}+\angle \mathrm{CAD}=90^{\circ}$

या, $\quad\angle \mathrm{BAD}=90^{\circ}$

इसलिए, $\mathrm{ABCD}$ एक समांतर चतुर्भुज है जिसमें एक कोण $90^{\circ}$ है।
इसलिए, $\mathrm{ABCD}$ एक आयत है।

उदाहरण 5 : दिखाइए कि एक समांतर चतुर्भुज के कोणों के समद्विभाजक एक आयत बनाते हैं।

हल : मान लीजिए $\mathrm{P}, \mathrm{Q}, \mathrm{R}$ और $\mathrm{S}$ समांतर चतुर्भुज $\mathrm{ABCD}$ के $\angle \mathrm{A}$ और $\angle \mathrm{B}$, $\angle \mathrm{B}$ और $\angle \mathrm{C}$, $\angle \mathrm{C}$ और $\angle \mathrm{D}$, और $\angle \mathrm{D}$ और $\angle \mathrm{A}$ के समद्विभाजकों के प्रतिच्छेद बिंदु हैं (देखिए आकृति 8.10)।

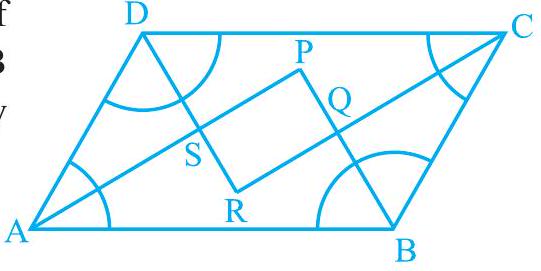
आकृति 8.10

$\triangle \mathrm{ASD}$ में, आप क्या देखते हैं?

चूँकि $\mathrm{DS}$, $\angle \mathrm{D}$ का समद्विभाजक है और $\mathrm{AS}$, $\angle \mathrm{A}$ का समद्विभाजक है, इसलिए,

$$ \begin{aligned} \angle \mathrm{DAS}+\angle \mathrm{ADS} & =\frac{1}{2} \angle \mathrm{A}+\frac{1}{2} \angle \mathrm{D} \ & =\frac{1}{2}(\angle \mathrm{A}+\angle \mathrm{D}) \ & =\frac{1}{2} \times 180^{\circ} \ (\angle \mathrm{A} \text { और } & \angle \mathrm{D} \text{ एक ही तिर्यक रेखा के एक ही ओर की आंतरिक कोण हैं} \ & \left.=90^{\circ} \quad \right) \end{aligned} $$

साथ ही, $\angle \mathrm{DAS}+\angle \mathrm{ADS}+\angle \mathrm{DSA}=180^{\circ} \quad$ (त्रिभुज का कोण योग गुणधर्म)

या,$\quad 90^{\circ}+\angle \mathrm{DSA}=180^{\circ}$

या,$\quad \angle \mathrm{DSA}=90^{\circ}$

इसलिए,$\quad \angle \mathrm{PSR}=90^{\circ} \quad$($\angle \mathrm{DSA}$ के शीर्षाभिमुख होने के कारण)

इसी प्रकार, यह दिखाया जा सकता है कि $\angle \mathrm{APB}=90^{\circ}$ या $\angle \mathrm{SPQ}=90^{\circ}$ (जैसा $\angle \mathrm{DSA}$ के लिए दिखाया गया था)। इसी प्रकार, $\angle \mathrm{PQR}=90^{\circ}$ और $\angle \mathrm{SRQ}=90^{\circ}$।

इसलिए, PQRS एक चतुर्भुज है जिसमें सभी कोण समकोण हैं।

क्या हम निष्कर्ष निकाल सकते हैं कि यह एक आयत है? आइए परीक्षण करें। हमने दिखाया है कि ∠PSR = ∠PQR = 90° और ∠SPQ = ∠SRQ = 90°। इसलिए विपरीत कोणों के दोनों युग्म समान हैं।

इसलिए, PQRS एक समांतर चतुर्भुज है जिसमें एक कोण (वास्तव में सभी कोण) 90° है, और इसलिए PQRS एक आयत है।

8.2 मध्य-बिंदु प्रमेय

आपने एक त्रिभुज और एक चतुर्भुज के कई गुणों का अध्ययन किया है। अब आइए एक और परिणाम का अध्ययन करें जो त्रिभुज की भुजाओं के मध्य-बिंदुओं से संबंधित है। निम्नलिखित गतिविधि करें।

एक त्रिभुज बनाएं और उसकी दो भुजाओं के मध्य-बिंदुओं E और F को चिह्नित करें। बिंदुओं E और F को मिलाएं (देखें चित्र 8.15)।

EF और BC को मापें। ∠AEF और ∠ABC को मापें।

आप क्या देखते हैं? आप पाएंगे कि:

EF = ½ BC और ∠AEF = ∠ABC

इसलिए, EF || BC

इस गतिविधि को कुछ और त्रिभुजों के साथ दोहराएं।

इस प्रकार आप निम्नलिखित प्रमेय तक पहुँचते हैं:

प्रमेय 8.8: त्रिभुज की दो भुजाओं के मध्य-बिंदुओं को मिलाने वाला रेखाखंड तीसरी भुजा के समांतर होता है।

आप इस प्रमेय को निम्नलिखित संकेत का उपयोग कर सिद्ध कर सकते हैं:

ध्यान दीजिए चित्र 8.16 पर जिसमें $E$ और $F$ क्रमशः $\mathrm{AB}$ और $\mathrm{AC}$ के मध्य-बिंदु हैं और $\mathrm{CD} || \mathrm{BA}$ है।

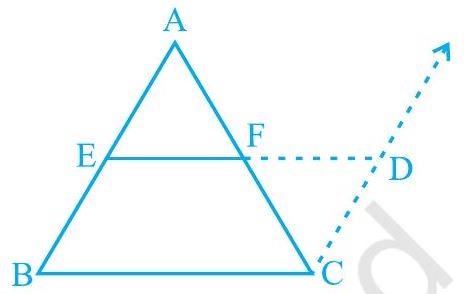
चित्र 8.16

$ \begin{equation*} \Delta \mathrm{AEF} \cong \triangle \mathrm{CDF} \tag{ASAनियम} \end{equation*} $

इसलिए, $\quad \mathrm{EF}=\mathrm{DF}$ और $\mathrm{BE}=\mathrm{AE}=\mathrm{DC} \quad($ क्यों? $)$

इसलिए, BCDE एक समांतर चतुर्भुज है। (क्यों?)

इससे प्राप्त होता है $\mathrm{EF} || \mathrm{BC}$।

इस स्थिति में, यह भी ध्यान दीजिए कि $\mathrm{EF}=\frac{1}{2} \mathrm{ED}=\frac{1}{2} \mathrm{BC}$।

क्या आप प्रमेय 8.8 का व्युत्क्रम कह सकते हैं? क्या व्युत्क्रम सत्य है?

आप देखेंगे कि उपरोक्त प्रमेय का व्युत्क्रम भी सत्य है जो नीचे दिया गया है:

प्रमेय 8.9 : त्रिभुज की एक भुजा के मध्य-बिंदु से होकर खींची गई रेखा, जो दूसरी भुजा के समांतर होती है, तीसरी भुजा को समद्विभाजित करती है।

चित्र 8.17 में, ध्यान दीजिए कि $\mathrm{E}$ भुजा $\mathrm{AB}$ का मध्य-बिंदु है, रेखा $l$ बिंदु $\mathrm{E}$ से होकर गुजर रही है और $\mathrm{BC}$ के समांतर है और $\mathrm{CM} || \mathrm{BA}$ है।

सिद्ध कीजिए कि $\mathrm{AF}=\mathrm{CF}$ है, $\triangle \mathrm{AEF}$ और $\triangle \mathrm{CDF}$ की सर्वांगसमता का उपयोग करके।

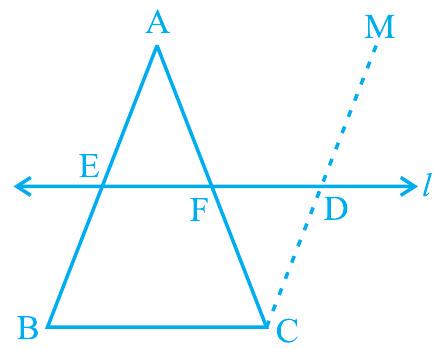
आकृति 8.17

उदाहरण 6 : $\triangle \mathrm{ABC}$ में, $\mathrm{D}, \mathrm{E}$ और $\mathrm{F}$ क्रमशः भुजाओं $\mathrm{AB}, \mathrm{BC}$ और $\mathrm{CA}$ के मध्य-बिंदु हैं (आकृति 8.18 देखें)। दिखाइए कि $\mathrm{D}, \mathrm{E}$ और $\mathrm{F}$ को मिलाने से $\triangle \mathrm{ABC}$ चार सर्वांगसम त्रिभुजों में विभाजित हो जाता है।

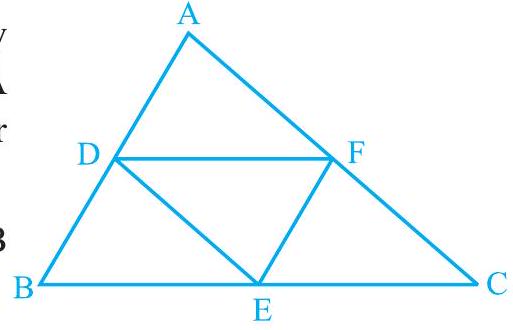
आकृति 8.18

हल : चूँकि D और E त्रिभुज $\mathrm{ABC}$ की भुजाओं AB और $\mathrm{BC}$ के मध्य-बिंदु हैं, प्रमेय 8.8 द्वारा,

इसी प्रकार, $\quad \quad \mathrm{DF} || \mathrm{BC}$ और $\mathrm{EF} || \mathrm{AB}$

इसलिए ADEF, BDFE और DFCE सभी समांतर चतुर्भुज हैं।

अब $\mathrm{DE}$ समांतर चतुर्भुज $\mathrm{BDFE}$ का एक विकर्ण है,

इसलिए, $\quad \Delta \mathrm{BDE} \cong \Delta \mathrm{FED}$

इसी प्रकार $\quad \Delta \mathrm{DAF} \cong \triangle \mathrm{FED}$

और $\quad \Delta \mathrm{EFC} \cong \triangle \mathrm{FED}$

इस प्रकार, सभी चार त्रिभुज सर्वांगसम हैं।

उदाहरण 7 : $ l, m$ और $n$ तीन समानांतर रेखाएँ हैं जिन्हें अनुप्रस्थ रेखाएँ $p$ और $q$ काटती हैं इस प्रकार कि $l, m$ और $n$, $p$ पर समान अंतराल $\mathrm{AB}$ और $\mathrm{BC}$ काटती हैं (देखिए आकृति 8.19)। दिखाइए कि $l, m$ और $n$, $q$ पर भी समान अंतराल $\mathrm{DE}$ और $\mathrm{EF}$ काटती हैं।

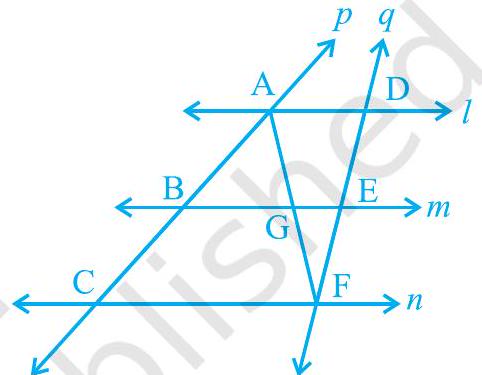
आकृति 8.19

हल : हमें दिया गया है कि $\mathrm{AB}=\mathrm{BC}$ और हमें यह सिद्ध करना है कि $\mathrm{DE}=\mathrm{EF}$।

आइए बिंदु $\mathrm{A}$ को $\mathrm{F}$ से इस प्रकार जोड़ें कि यह $m$ को $\mathrm{G}$ पर काटे।

समलंब ACFD को दो त्रिभुजों में विभाजित किया गया है;

अर्थात् $\triangle \mathrm{ACF}$ और $\triangle \mathrm{AFD}$।

$\triangle \mathrm{ACF}$ में, दिया गया है कि $\mathrm{B}$, $\mathrm{AC}$ का मध्य-बिंदु है ($\mathrm{AB}=\mathrm{BC}$)

और $\quad \mathrm{BG} || \mathrm{CF} \quad($ चूँकि $m || n)$।

अतः, $\mathrm{G}$, AF का मध्य-बिंदु है (प्रमेय 8.9 का उपयोग करके)

अब, $\triangle$ AFD में, हम वही तर्क लगा सकते हैं कि चूँकि $G$, AF का मध्य-बिंदु है, $\mathrm{GE} || \mathrm{AD}$ और इसलिए प्रमेय $8.9$ से, $\mathrm{E}$, $\mathrm{DF}$ का मध्य-बिंदु है,

अर्थात्,$\quad\mathrm{DE}=\mathrm{EF}$।

दूसरे शब्दों में, $l, m$ और $n$, $q$ पर भी समान अंतराल काटती हैं।

8.3 सारांश

इस अध्याय में, आपने निम्नलिखित बिंदुओं का अध्ययन किया है :

1. समांतर चतुर्भुज का एक विकर्ण उसे दो सर्वांगसम त्रिभुजों में विभाजित करता है।

2. एक समांतर चतुर्भुज में,

(i) विपरीत भुजाएँ बराबर होती हैं

(ii) विपरीत कोण बराबर होते हैं

(iii) विकर्ण एक-दूसरे को समद्विभाजित करते हैं

3. आयत के विकर्ण एक-दूसरे को समद्विभाजित करते हैं और बराबर होते हैं और इसका विलोम भी सत्य है।

4. समचतुर्भुज के विकर्ण एक-दूसरे को समकोण पर समद्विभाजित करते हैं और इसका विलोम भी सत्य है।

5. वर्ग के विकर्ण एक-दूसरे को समकोण पर समद्विभाजित करते हैं और बराबर होते हैं, और इसका विलोम भी सत्य है।

6. किसी त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिंदुओं को मिलाने वाला रेखाखंड तीसरी भुजा के समांतर होता है और उसकी आधी लंबाई का होता है।

7. किसी त्रिभुज की एक भुजा के मध्य-बिंदु से होकर जाने वाली रेखा, यदि दूसरी भुजा के समांतर हो, तो तीसरी भुजा को समद्विभाजित करती है।