7.1 परिचय

आपने अपनी पिछली कक्षाओं में त्रिभुजों और उनके विभिन्न गुणों के बारे में पढ़ा है। आप जानते हैं कि तीन प्रतिच्छेदी रेखाओं द्वारा बनाया गया एक बंद आकृति त्रिभुज कहलाता है। (‘Tri’ का अर्थ है ‘तीन’)। एक त्रिभुज के तीन भुजाएँ, तीन कोण और तीन शीर्ष होते हैं। उदाहरण के लिए, त्रिभुज $\mathrm{ABC}$ में, जिसे $\triangle \mathrm{ABC}$ के रूप में दर्शाया गया है (देखें Fig. 7.1); $\mathrm{AB}, \mathrm{BC}, \mathrm{CA}$ तीन भुजाएँ हैं, $\angle \mathrm{A}, \angle \mathrm{B}, \angle \mathrm{C}$ तीन कोण हैं और $\mathrm{A}, \mathrm{B}, \mathrm{C}$ तीन शीर्ष हैं। अध्याय 6 में, आपने त्रिभुजों के कुछ गुणों का भी अध्ययन किया है। इस अध्याय में, आप त्रिभुजों की सर्वांगसमता, सर्वांगसमता के नियमों, त्रिभुजों के कुछ और गुणों और त्रिभुज में असमानताओं के बारे में विस्तार से पढ़ेंगे। आपने इनमें से अधिकांश गुणों को पहले ही पिछली कक्षाओं में सत्यापित किया है। अब हम इनमें से कुछ को सिद्ध करेंगे।

7.2 त्रिभुजों की सर्वांगसमता

Fig. 7.1

आपने अवश्य देखा होगा कि आपकी एक ही आकार की फोटोग्राफ़ की दो प्रतियाँ समान होती हैं। इसी प्रकार, एक ही आकार की दो चूड़ियाँ, एक ही बैंक द्वारा जारी किए गए दो एटीएम कार्ड समान होते हैं। आपको याद होगा कि एक रुपये का सिक्का उसी वर्ष में ढाला गया दूसरे सिक्के पर रखने पर वे एक-दूसरे को पूरी तरह ढक लेते हैं।

क्या आपको याद है कि ऐसी आकृतियों को क्या कहा जाता है? वास्तव में इन्हें सर्वांगसम आकृतियाँ कहा जाता है (‘सर्वांगसम’ का अर्थ है सभी दृष्टियों से बराबर या ऐसी आकृतियाँ जिनकी आकृति और आकार दोनों समान हों)।

अब, समान त्रिज्या के दो वृत्त खींचो और एक को दूसरे के ऊपर रखो। तुम क्या देखते हो? वे एक-दूसरे को पूरी तरह ढक लेते हैं और हम उन्हें सर्वांगसम वृत्त कहते हैं।

इस क्रियाकलाप को दोहराओ, एक वर्ग को दूसरे वर्ग के ऊपर रखकर जिनकी भुजाएँ समान हों (देखो चित्र 7.2) या दो समभुज त्रिभुजों को समान भुजाओं के साथ एक-दूसरे के ऊपर रखकर। तुम देखोगे कि वर्ग एक-दूसरे के सर्वांगसम हैं और समभुज त्रिभुज भी ऐसे ही हैं।

चित्र 7.2

तुम्हें आश्चर्य हो रहा होगा कि हम सर्वांगसमता क्यों पढ़ रहे हैं। तुम सभी ने अपने रेफ्रिजरेटर में बर्फ की ट्रे देखी होगी। देखो कि बर्फ बनाने के लिए बने सांचे सभी सर्वांगसम हैं। ट्रे में ढालने के लिए प्रयुक्त ढांचे में भी सर्वांगसम गड्ढे होते हैं (शायद सभी आयताकार या सभी वृत्ताकार या सभी त्रिकोणीय)। इसलिए, जब भी समान वस्तुओं का उत्पादन करना हो, ढांचा बनाने में सर्वांगसमता की अवधारणा का प्रयोग किया जाता है।

कभी-कभी, तुम्हें अपने पेन में रिफिल बदलने में कठिनाई हो सकती है और ऐसा तब होता है जब नई रिफिल उस रिफिल के समान आकार की नहीं होती जिसे तुम निकालना चाहते हो। स्पष्ट है, यदि दोनों रिफिल समान या सर्वांगसम हों, तो नई रिफिल फिट बैठती है।

इसलिए, आप दैनिक जीवन की परिस्थितियों में वस्तुओं की सर्वांगसमता के अनुप्रयोग के असंख्य उदाहरण पा सकते हैं।

क्या आप सर्वांगसम आकृतियों के कुछ और उदाहरण सोच सकते हैं?

अब, निम्नलिखित में से कौन-सी आकृतियाँ आकृति 7.3 (i) में दिए गए वर्ग के सर्वांगसम नहीं हैं:

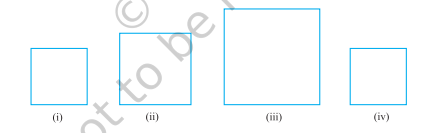
आकृति 7.3

आकृति 7.3 (ii) और (iii) में दिए गए बड़े वर्ग स्पष्ट रूप से आकृति 7.3 (i) में दिए गए वर्ग के सर्वांगसम नहीं हैं, लेकिन आकृति 7.3 (iv) में दिया गया वर्ग आकृति 7.3 (i) में दिए गए वर्ग के सर्वांगसम है।

आइए अब हम दो त्रिभुजों की सर्वांगसमता पर चर्चा करें।

आप पहले से जानते हैं कि दो त्रिभुज तभी सर्वांगसम होते हैं जब एक त्रिभुज की भुजाएँ और कोण दूसरे त्रिभुज की संगत भुजाओं और कोणों के बराबर हों।

अब, नीचे दी गई त्रिभुजों में से कौन-सी त्रिभुज आकृति 7.4 (i) में दी गई त्रिभुज ABC के सर्वांगसम हैं?

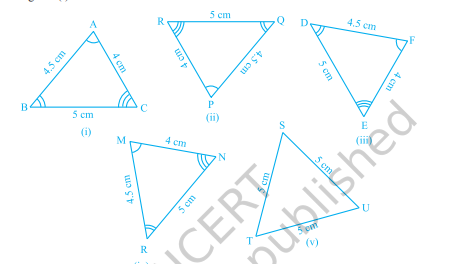
आकृति 7.4

आकृति 7.4 (ii) से (v) तक की इन त्रिभुजों को काटकर उन्हें घुमाइए और त्रिभुज ABC को ढकने का प्रयास कीजिए। देखिए कि आकृति 7.4 (ii), (iii) और (iv) की त्रिभुजें त्रिभुज ABC के सर्वांगसम हैं जबकि आकृति 7.4 (v) की त्रिभुज TSU त्रिभुज ABC के सर्वांगसम नहीं है।

यदि $\triangle \mathrm{PQR}$ सर्वांगसम है $\triangle \mathrm{ABC}$ से, तो हम लिखते हैं $\Delta \mathrm{PQR} \cong \triangle \mathrm{ABC}$।

ध्यान दीजिए कि जब $\Delta \mathrm{PQR} \cong \triangle \mathrm{ABC}$ होता है, तब $\Delta \mathrm{PQR}$ की भुजाएँ $\triangle \mathrm{ABC}$ की संगत बराबर भुजाओं पर आ जाती हैं और कोणों के साथ भी ऐसा ही होता है।

अर्थात्, $\mathrm{PQ}$ आच्छादित करता है $\mathrm{AB}$ को, $\mathrm{QR}$ आच्छादित करता है $\mathrm{BC}$ को और $\mathrm{RP}$ आच्छादित करता है $\mathrm{CA}$ को; $\angle \mathrm{P}$ आच्छादित करता है $\angle \mathrm{A}$ को, $\angle \mathrm{Q}$ आच्छादित करता है $\angle \mathrm{B}$ को और $\angle \mathrm{R}$ आच्छादित करता है $\angle \mathrm{C}$ को। साथ ही, शीर्षों के बीच एक-एक संगति होती है। अर्थात्, $\mathrm{P}$ संगत है $\mathrm{A}$ से, $\mathrm{Q}$ से $\mathrm{B}$ से, $\mathrm{R}$ से $\mathrm{C}$ से और आगे जो इस प्रकार लिखा जाता है

$$\mathrm{P} \leftrightarrow \mathrm{A}, \mathrm{Q} \leftrightarrow \mathrm{B},\mathrm{R} \leftrightarrow \mathrm{C}$$

ध्यान दीजिए कि इस संगति के अंतर्गत, $\triangle \mathrm{PQR} \cong \triangle \mathrm{ABC}$ है; परंतु यह सही नहीं होगा कि $\Delta \mathrm{QRP} \cong \triangle \mathrm{ABC}$ लिखा जाए।

इसी प्रकार, आकृति 7.4 (iii) के लिए,

$$\mathrm{FD} \leftrightarrow \mathrm{AB}, \mathrm{DE} \leftrightarrow \mathrm{BC} \text { और } \mathrm{EF} \leftrightarrow \mathrm{CA} $$

$ \text { और } \mathrm{F} \leftrightarrow \mathrm{A}, \mathrm{D} \leftrightarrow \mathrm{B} \text { और } \mathrm{E} \leftrightarrow \mathrm{C}$ इसलिए, $\Delta \mathrm{FDE} \cong \triangle \mathrm{ABC}$ लेकिन $\Delta \mathrm{DEF} \cong \Delta \mathrm{ABC}$ लिखना सही नहीं है।

आकृति 7.4 (iv) में दिए गए त्रिभुज और $\triangle \mathrm{ABC}$ के बीच संगतता बताइए।

इसलिए, त्रिभुजों की सर्वांगसमता को प्रतीकात्मक रूप में लिखने के लिए शीर्षों की संगतता को सही ढंग से लिखना आवश्यक है।

ध्यान दें कि सर्वांगसम त्रिभुजों में संगत भाग समान होते हैं और हम संक्षेप में इसे ’ $\mathrm{CPCT}$ ’ लिखते हैं, जिसका अर्थ है सर्वांगसम त्रिभुजों के संगत भाग।

7.3 त्रिभुजों की सर्वांगसमता के मानदंड

पिछली कक्षाओं में, आप त्रिभुजों की सर्वांगसमता के चार मानदंड सीख चुके हैं। आइए उन्हें याद करें।

दो त्रिभुज बनाइए जिनकी एक भुजा $3 \mathrm{~cm}$ हो। क्या ये त्रिभुज सर्वांगसम हैं? देखिए कि वे सर्वांगसम नहीं हैं (आकृति 7.5 देखें)।

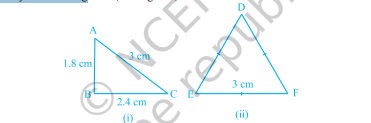
आकृति 7.5

अब, दो त्रिभुज बनाइए जिनकी एक भुजा $4 \mathrm{~cm}$ और एक कोण $50^{\circ}$ हो (आकृति 7.6 देखें)। क्या वे सर्वांगसम हैं?

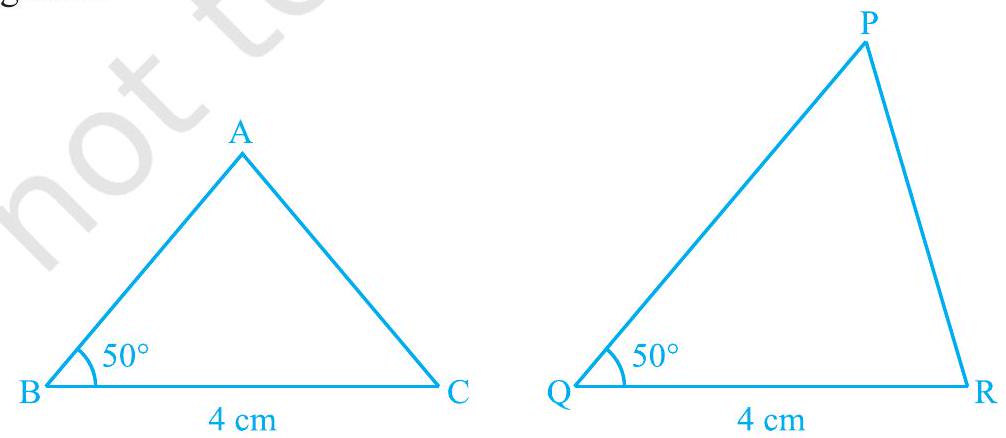
आकृति 7.6

देखिए कि ये दो त्रिभुज सर्वांगसम नहीं हैं।

इस क्रियाकलाप को कुछ और त्रिभुजों के युगलों के साथ दोहराइए।

इसलिए, एक युगल भुजाओं या एक युगल भुजाओं और एक युगल कोणों की समानता हमें सर्वांगसम त्रिभुज देने के लिए पर्याप्त नहीं है।

यदि समान कोणों की अन्य भुजाओं (भुजाओं) का युगल भी समान हो तो क्या होगा?

चित्र 7.7 में, $\mathrm{BC}=\mathrm{QR}, \angle \mathrm{B}=\angle \mathrm{Q}$ और साथ ही, $\mathrm{AB}=\mathrm{PQ}$। अब, आप $\triangle \mathrm{ABC}$ और $\triangle \mathrm{PQR}$ की सर्वांगसमता के बारे में क्या कह सकते हैं?

अपनी पिछली कक्षाओं से याद कीजिए कि, इस स्थिति में, दोनों त्रिभुज सर्वांगसम होते हैं। चित्र 7.7 में $\triangle \mathrm{ABC}$ और $\triangle \mathrm{PQR}$ के लिए इसकी पुष्टि कीजिए। इस क्रियाकलाप को अन्य त्रिभुजों के युगलों के साथ दोहराइए। क्या आपने देखा कि दो भुजाओं और अंतर्वर्ती कोण की समानता त्रिभुजों की सर्वांगसमता के लिए पर्याप्त है? हाँ, यह पर्याप्त है।

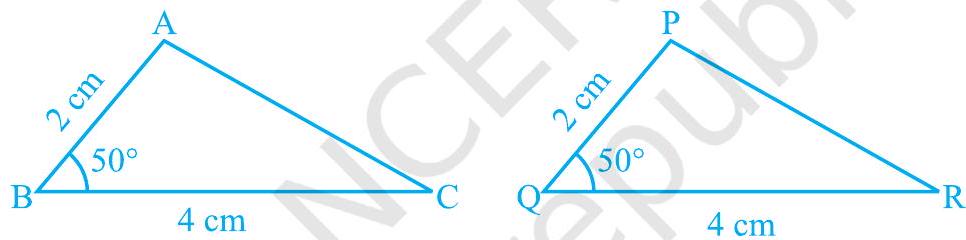
चित्र 7.7

यह त्रिभुजों की सर्वांगसमता का पहला मानदंड है।

अभिगृहित 7.1 (SAS सर्वांगसमता नियम) : दो त्रिभुज सर्वांगसम होते हैं यदि एक त्रिभुज की दो भुजाएँ और अंतर्वर्ती कोण दूसरे त्रिभुज की दो भुजाओं और अंतर्वर्ती कोण के समान हों।

इस परिणाम को पहले से ज्ञात परिणामों की सहायता से सिद्ध नहीं किया जा सकता और इसलिए इसे एक अभिगृहित के रूप में सत्य माना जाता है (परिशिष्ट 1 देखें)।

आइए अब कुछ उदाहरण लेते हैं।

उदाहरण 1 : आकृति 7.8 में, $\mathrm{OA}=\mathrm{OB}$ और $\mathrm{OD}=\mathrm{OC}$ है। दिखाइए कि

(i) $\triangle \mathrm{AOD} \cong \triangle \mathrm{BOC}$ और

(ii) $\mathrm{AD} || \mathrm{BC}$.

हल : (i) आप देख सकते हैं कि $\triangle \mathrm{AOD}$ और $\triangle \mathrm{BOC}$ में,

$OA=OB\quad \text {(दिया गया है)}$

$OD=OC\quad \text {(दिया गया है)}$

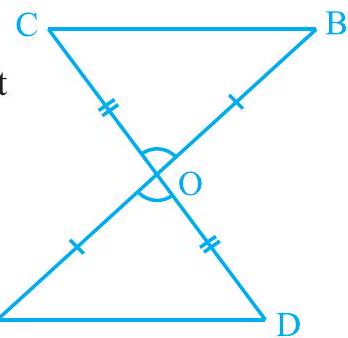
आकृति 7.8

इसके अलावा, चूँकि $\angle \mathrm{AOD}$ और $\angle \mathrm{BOC}$ एक युग्म शीर्षाभिमुख कोण बनाते हैं, हमारे पास

$\quad \quad$ $\angle \mathrm{AOD}=\angle \mathrm{BOC}$ है।

अतः, $\quad$ $\triangle \mathrm{AOD} \cong \triangle \mathrm{BOC} \quad$ (SAS सर्वांगसमता नियम से)

(ii) सर्वांगसम त्रिभुजों $\mathrm{AOD}$ और $\mathrm{BOC}$ में, अन्य संगत भाग भी समान होते हैं।

अतः, $\quad$ $\angle \mathrm{OAD}=\angle \mathrm{OBC}$ और ये रेखाखंडों $\mathrm{AD}$ और $\mathrm{BC}$ के लिए एक युग्म वैकल्पिक कोण बनाते हैं।

इसलिए,$\quad$$\mathrm{AD} || \mathrm{BC}$।

उदाहरण 2 : AB एक रेखाखंड है और रेखा $l$ इसका लंब समद्विभाजक है। यदि कोई बिंदु $\mathrm{P}$, $l$ पर स्थित है, तो दिखाइए कि $\mathrm{P}$, $\mathrm{A}$ और $\mathrm{B}$ से समदूरस्थ है।

हल: रेखा (l \perp \mathrm{AB}) और बिंदु (\mathrm{C}) से होकर जाती है जो (\mathrm{AB}) का मध्य-बिंदु है (देखिए आकृति 7.9)। आपको दिखाना है कि (\mathrm{PA}=\mathrm{PB}) है। (\triangle \mathrm{PCA}) और (\triangle \mathrm{PCB}) पर विचार कीजिए।

हमारे पास (\quad \mathrm{AC}=\mathrm{BC} \quad(\mathrm{C}, \mathrm{AB}) का मध्य-बिंदु है)

( \angle \mathrm{PCA}=\angle \mathrm{PCB}=90^{\circ} \text { (दिया गया है) } )

(\mathrm{PC} =\mathrm{PC} \quad \text {(उभयनिष्ठ)})

इसलिए, (\quad \triangle \mathrm{PCA} \cong \triangle \mathrm{PCB}) (SAS नियम)

और इसलिए, (\mathrm{PA}=\mathrm{PB}), क्योंकि ये सर्वांगसम त्रिभुजों की संगत भुजाएँ हैं।

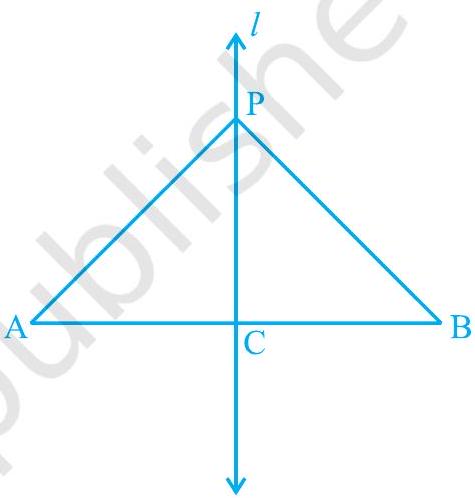
आकृति 7.9

अब, आइए दो त्रिभुजों की रचना करें, जिनकी भुजाएँ (4 \mathrm{~cm}) और (5 \mathrm{~cm}) हैं और एक कोण (50^{\circ}) है और यह कोण समान भुजाओं के बीच में स्थित नहीं है (देखिए आकृति 7.10)। क्या ये दोनों त्रिभुज सर्वांगसम हैं?

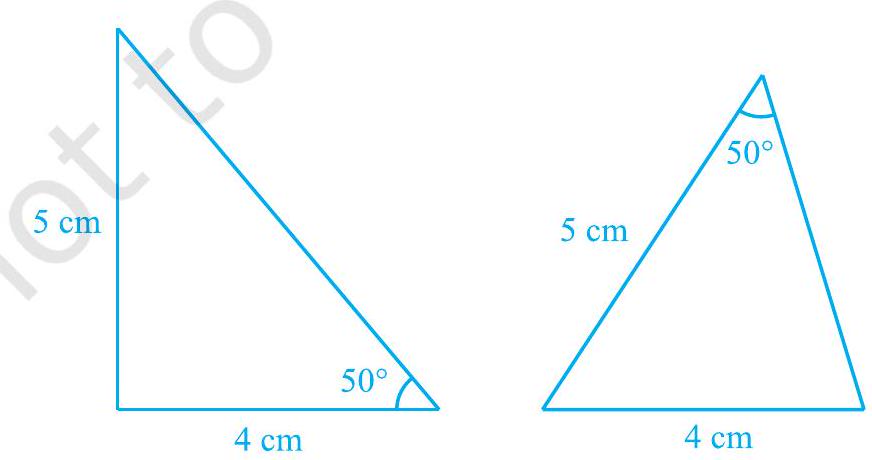
आकृति 7.10

ध्यान दीजिए कि ये दोनों त्रिभुज सर्वांगसम नहीं हैं।

इस क्रिया को और अधिक त्रिभुजों के युगलों के साथ दोहराएँ। आप देखेंगे कि त्रिभुजों के सर्वांगसम होने के लिए यह अत्यंत आवश्यक है कि बराबर कोण बराबर भुजाओं के युगलों के बीच सम्मिलित हों।

इसलिए SAS सर्वांगसमता नियम लागू होता है, परंतु ASS या SSA नियम नहीं।

अगला, उन दो त्रिभुजों की रचना करने का प्रयास करें जिनमें दो कोण क्रमशः (60^{\circ}) और (45^{\circ}) हैं और इन कोणों के बीच सम्मिलित भुजा की लंबाई (4 \mathrm{~cm}) है (देखें आकृति 7.11)।

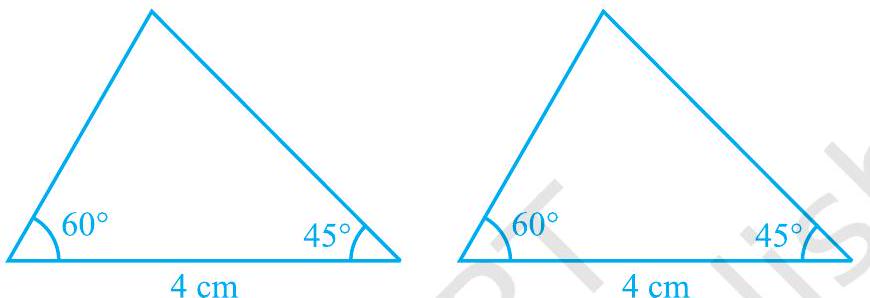
आकृति 7.11

इन त्रिभुजों को काटकर एक त्रिभुज को दूसरे के ऊपर रखें। आप क्या प्रेक्षित करते हैं? देखें कि एक त्रिभुज दूसरे को पूरी तरह ढक लेता है; अर्थात् दोनों त्रिभुज सर्वांगसम हैं। इस क्रिया को और अधिक त्रिभुजों के युगलों के साथ दोहराएँ। आप देखेंगे कि दो कोणों और सम्मिलित भुजा की समानता त्रिभुजों की सर्वांगसमता के लिए पर्याप्त है।

यह परिणाम सर्वांगसमता का कोण-भुजा-कोण मानदंड है और इसे ASA मानदंड लिखा जाता है। आपने इस मानदंड को पिछली कक्षाओं में सत्यापित किया है, परंतु आइए इसे कथनित करें और सिद्ध करें।

चूँकि इस परिणाम को सिद्ध किया जा सकता है, इसे प्रमेय कहा जाता है और इसे सिद्ध करने के लिए हम सर्वांगसमता के SAS अभिगृहित का उपयोग करते हैं।

प्रमेय 7.1 (ASA सर्वांगसमता नियम): दो त्रिभुज सर्वांगसम होते हैं यदि एक त्रिभुज के दो कोण और सम्मिलित भुजा दूसरे त्रिभुज के दो कोणों और सम्मिलित भुजा के बराबर हों।

प्रमाण: हमें दो त्रिभुजें ABC और DEF दी गई हैं जिनमें:

∠B = ∠E, ∠C = ∠F

और BC = EF

हमें यह सिद्ध करना है कि △ABC ≅ △DEF

दो त्रिभुजों की सर्वांगसमता सिद्ध करने के लिए देखिए कि तीन स्थितियाँ उत्पन्न होती हैं।

स्थिति (i): मान लीजिए AB = DE (देखिए आकृति 7.12)।

अब आप क्या देखते हैं? आप देख सकते हैं कि

AB = DE (मान लिया गया) ∠B = ∠E (दिया गया) BC = EF (दिया गया) △ABC ≅ △DEF (SAS नियम से)

इसलिए,

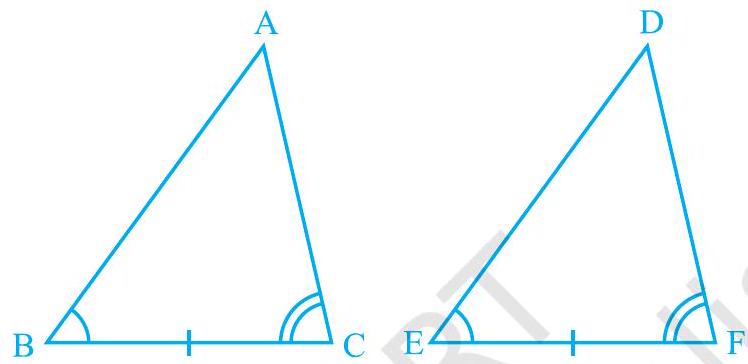
आकृति 7.12

स्थिति (ii): यदि संभव हो तो मान लीजिए AB > DE। इसलिए, हम AB पर एक बिंदु P इस प्रकार ले सकते हैं कि PB = DE। अब △PBC और △DEF पर विचार कीजिए (देखिए आकृति 7.13)।

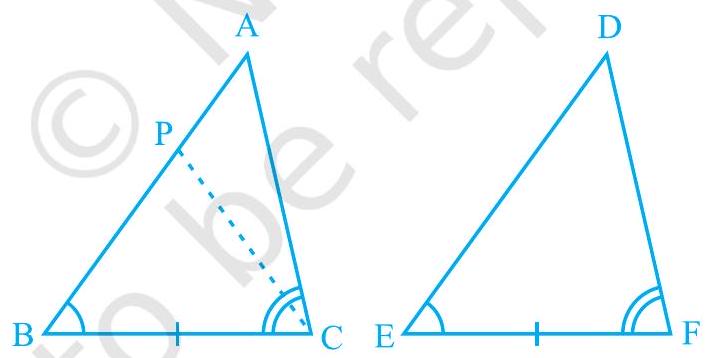
आकृति 7.13

ध्यान दीजिए कि △PBC और △DEF में,

$$ \begin{aligned} & \mathrm{PB}=\mathrm{DE} \quad \text {(रचना द्वारा)} \\ & \angle \mathrm{B}=\angle \mathrm{E} \quad \text {(दिया है)} \\ & \mathrm{BC}=\mathrm{EF} \quad \text {(दिया है)} \end{aligned} $$

इसलिए, हम निष्कर्ष निकाल सकते हैं कि:

$\Delta \mathrm{PBC} \cong \triangle \mathrm{DEF}$, सर्वांगसमता के लिए SAS अभिगृहित द्वारा।

चूँकि त्रिभुज सर्वांगसम हैं, उनके संगत भाग बराबर होंगे।

इसलिए, $\quad \angle \mathrm{PCB}=\angle \mathrm{DFE}$

लेकिन, हमें दिया गया है कि

$\quad\ \quad \angle \mathrm{ACB}=\angle \mathrm{DFE}$

क्या यह संभव है?

यह तभी संभव है जब $\mathrm{P}$, $\mathrm{A}$ के संपाती हो।

या,$\quad\mathrm{BA}=\mathrm{ED}$

इसलिए,$\quad \Delta \mathrm{ABC} \cong \Delta \mathrm{DEF} \quad \text {(SAS अभिगृहित द्वारा)}$

स्थिति (iii) : यदि $\mathrm{AB}<\mathrm{DE}$, हम $\mathrm{DE}$ पर एक बिंदु $\mathrm{M}$ चुन सकते हैं ताकि $\mathrm{ME}=\mathrm{AB}$ हो और स्थिति (ii) में दिए गए तर्कों को दोहराकर हम निष्कर्ष निकाल सकते हैं कि $\mathrm{AB}=\mathrm{DE}$ और इस प्रकार, $\triangle \mathrm{ABC} \cong \triangle \mathrm{DEF}$।

मान लीजिए, अब दो त्रिभुजों में कोणों के दो युग्म और संगत भुजाओं का एक युग्म बराबर हैं लेकिन भुजा संगत बराबर कोणों के युग्मों के बीच सम्मिलित नहीं है। क्या त्रिभुज अभी भी सर्वांगसम हैं? आप देखेंगे कि वे सर्वांगसम हैं। क्या आप तर्क दे सकते हैं क्यों?

आप जानते हैं कि एक त्रिभुज के तीन कोणों का योग $180^{\circ}$ होता है। इसलिए यदि कोणों के दो युग्म समान हों, तो तीसरा युग्म भी समान होगा $\left(180^{\circ}-\right.$ समान कोणों का योग $)$।

इसलिए, दो त्रिभुज सर्वांगसम होते हैं यदि कोणों के किन्हीं दो युग्म और एक संगत भुजा का युग्म समान हो। हम इसे AAS सर्वांगसमता नियम कह सकते हैं।

अब आइए निम्नलिखित क्रियाकलाप करें :

$40^{\circ}$, $50^{\circ}$ और $90^{\circ}$ कोणों वाले त्रिभुज बनाइए। आप ऐसे कितने त्रिभुज बना सकते हैं?

वास्तव में, आप भुजाओं की विभिन्न लंबाइयों के साथ जितने चाहें उतने त्रिभुज बना सकते हैं (देखिए आकृति 7.14)।

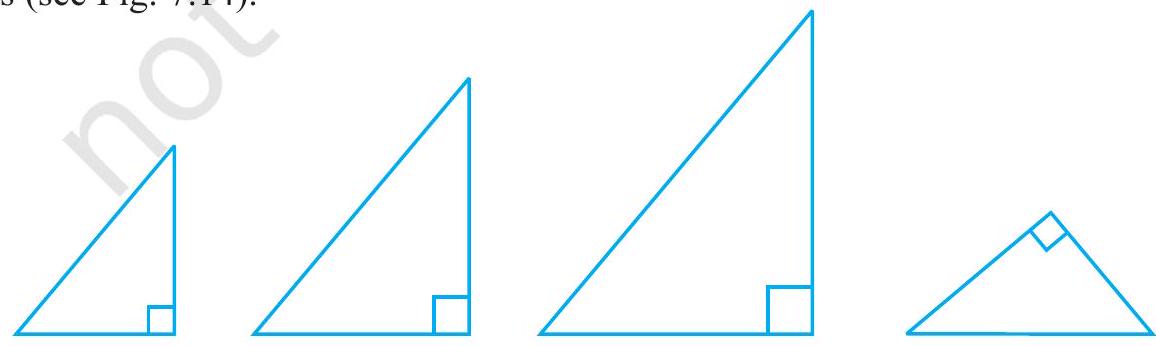
आकृति 7.14

ध्यान दीजिए कि त्रिभुज एक-दूसरे से सर्वांगसम हो भी सकते हैं और नहीं भी।

इसलिए, तीन कोणों की समानता त्रिभुजों की सर्वांगसमता के लिए पर्याप्त नहीं है। अतः त्रिभुजों की सर्वांगसमता के लिए तीन समान भागों में से एक भुजा होना चाहिए।

अब आइए कुछ और उदाहरण लें।

उदाहरण 3 : रेखाखंड $\mathrm{AB}$ दूसरे रेखाखंड $\mathrm{CD}$ के समांतर है। $\mathrm{O}$, $A D$ का मध्य-बिंदु है (देखिए आकृति 7.15)। दिखाइए कि (i) $\triangle A O B \cong \triangle D O C$ (ii) $O$, $\mathrm{BC}$ का भी मध्य-बिंदु है।

हल : (i) $\triangle \mathrm{AOB}$ और $\triangle \mathrm{DOC}$ पर विचार कीजिए।

$\quad \angle \mathrm{ABO}=\angle \mathrm{DCO}\quad$(एकांतर कोण क्योंकि $\mathrm{AB} || \mathrm{CD}$ और $\mathrm{BC}$ तिर्यक रेखा है)

$\quad \angle \mathrm{AOB}=\angle \mathrm{DOC}\quad$(शीर्षाभिमुख कोण)

$\quad \mathrm{OA}=\mathrm{OD}\quad$ (दिया है)

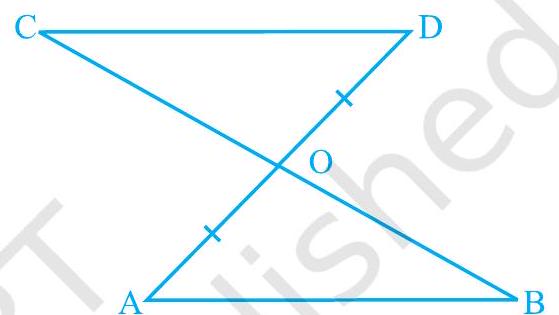
आकृति 7.15

इसलिए, $\quad \triangle \mathrm{AOB} \cong \triangle \mathrm{DOC} \quad$ (AAS नियम)

(ii) $\quad \mathrm{OB}=\mathrm{OC}\quad$(संगत भागों की समानता)

अतः, $\mathrm{O}$ बिंदु $\mathrm{BC}$ का मध्य-बिंदु है।

7.4 त्रिभुज के कुछ गुण

उपरोक्त खंड में आपने त्रिभुजों की सर्वांगसमता के दो मानदंड पढ़े हैं। आइए अब इन परिणामों का प्रयोग करके उन त्रिभुजों से संबंधित कुछ गुणों का अध्ययन करें जिनकी दो भुजाएँ समान हों।

नीचे दी गई गतिविधि करें:

एक ऐसा त्रिभुज बनाइए जिसकी दो भुजाएँ समान हों, मानों प्रत्येक $3.5 \mathrm{~cm}$ और तीसरी भुजा $5 \mathrm{cm}$ हो (देखें आकृति 7.24)। आपने ऐसी रचनाएँ पिछली कक्षाओं में की हैं।

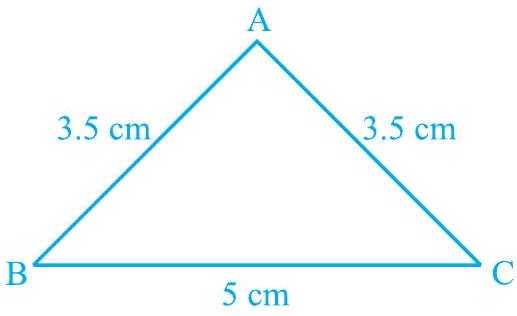
आकृति 7.24

क्या आपको याद है कि ऐसे त्रिभुज को क्या कहा जाता है?

एक त्रिभुज जिसकी दो भुजाएँ बराबर हों, समद्विबाहु त्रिभुज कहलाता है। इसलिए, चित्र 7.24 का $\triangle \mathrm{ABC}$ एक समद्विबाहु त्रिभुज है जिसमें $\mathrm{AB}=\mathrm{AC}$ है।

अब, $\angle \mathrm{B}$ और $\angle \mathrm{C}$ को मापिए। आप क्या देखते हैं?

इस क्रियाकलाप को भिन्न-भिन्न भुजाओं वाले अन्य समद्विबाहु त्रिभुजों के साथ दोहराइए।
आप देख सकते हैं कि प्रत्येक ऐसे त्रिभुज में, बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।

यह एक बहुत ही महत्वपूर्ण परिणाम है और वास्तव में किसी भी समद्विबाहु त्रिभुज के लिए सत्य है। इसे नीचे दिखाए अनुसार सिद्ध किया जा सकता है।

प्रमेय 7.2 : समद्विबाहु त्रिभुज की बराबर भुजाओं के सम्मुख कोण बराबर होते हैं। इस परिणाम को कई तरीकों से सिद्ध किया जा सकता है। यहाँ एक प्रमाण दिया गया है।

प्रमाण : हमें एक समद्विबाहु त्रिभुज $\mathrm{ABC}$ दिया गया है जिसमें $\mathrm{AB}=\mathrm{AC}$ है। हमें यह सिद्ध करना है कि $\angle \mathrm{B}=\angle \mathrm{C}$।
आइए $\angle \mathrm{A}$ का समद्विभाजक खींचें और मान लें कि $\mathrm{D}$ वह बिंदु है जहाँ यह समद्विभाजक $\angle \mathrm{A}$ और $\mathrm{BC}$ को काटता है (चित्र 7.25 देखिए)। $\Delta \mathrm{BAD}$ और $\Delta \mathrm{CAD}$ में,

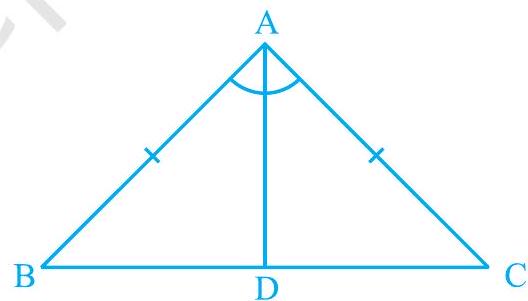
चित्र 7.25

$$ \begin{aligned} \mathrm{AB} & =\mathrm{AC} \quad \text {(दिया गया है)}\\ \angle \mathrm{BAD} & =\angle \mathrm{CAD} \quad \text {(रचना द्वारा)} \\ \mathrm{AD} & =\mathrm{AD} \quad \text {(उभयनिष्ठ)} \end{aligned} $$ $$ \text { इसलिए, } \quad \Delta \mathrm{BAD} \cong \Delta \mathrm{CAD} \quad \text {(SAS नियम द्वारा)} $$

इसलिए, $\angle \mathrm{ABD}=\angle \mathrm{ACD}$, क्योंकि ये सर्वांगसम त्रिभुजों के संगत कोण हैं।

इसलिए,$\quad \angle \mathrm{B}=\angle \mathrm{C}$

क्या विलोम भी सत्य है? अर्थात्:

क्या किसी त्रिभुज के दो कोण समान हों, तो क्या हम यह निष्कर्ष निकाल सकते हैं कि उनके सम्मुख भुजाएँ भी समान हैं?

निम्नलिखित क्रियाकलाप करें।

एक त्रिभुज $\mathrm{ABC}$ बनाइए जिसमें $\mathrm{BC}$ कोई लंबाई की हो और $\angle \mathrm{B}=\angle \mathrm{C}=50^{\circ}$। $\angle \mathrm{A}$ का समद्विभाजक खींचिए और इसे $\mathrm{BC}$ पर $\mathrm{D}$ पर मिलने दीजिए (देखिए आकृति 7.26)।

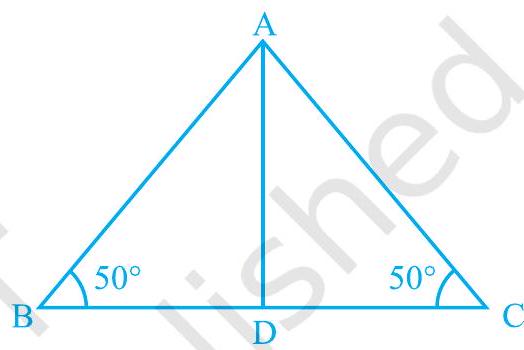
आकृति 7.26

कागज की शीट से त्रिभुज को काट लीजिए और इसे $\mathrm{AD}$ के साथ मोड़िए ताकि शीर्ष $\mathrm{C}$ शीर्ष B पर आ जाए।

आप भुजाओं $\mathrm{AC}$ और $\mathrm{AB}$ के बारे में क्या कह सकते हैं?

ध्यान दीजिए कि $\mathrm{AC}$ पूरी तरह $\mathrm{AB}$ को ढक लेती है

इसलिए,$\quad\mathrm{AC}=\mathrm{AB}$

इस क्रियाकलाप को कुछ और त्रिभुजों के साथ दोहराएं। हर बार आप देखेंगे कि समान कोणों के सम्मुख भुजाएं बराबर होती हैं। इसलिए हमारे पास निम्नलिखित है:

प्रमेय 7.3 : त्रिभुज के समान कोणों की सम्मुख भुजाएं बराबर होती हैं।

यह प्रमेय 7.2 का व्युत्क्रम है।

आप इस प्रमेय को ASA सर्वांगसमता नियम से सिद्ध कर सकते हैं। आइए इन परिणामों को लागू करने के लिए कुछ उदाहरण लें।

उदाहरण 4 : $\triangle \mathrm{ABC}$ में, $\angle \mathrm{A}$ का समद्विभाजक $\mathrm{AD}$ भुजा $\mathrm{BC}$ पर लंबवत है (देखिए चित्र 7.27)। दिखाइए कि $A B=A C$ और $\triangle A B C$ समद्विबाहु है।

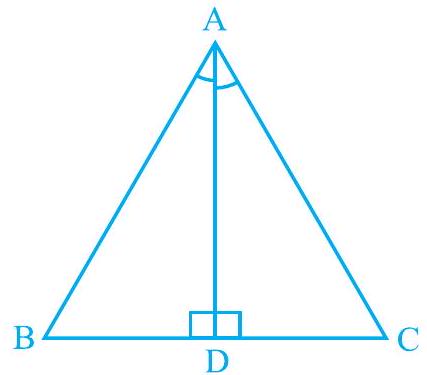
चित्र 7.27

हल : $\triangle \mathrm{ABD}$ और $\triangle \mathrm{ACD}$ में,

$$ \begin{aligned} \angle \mathrm{BAD} & =\angle \mathrm{CAD}\quad \text {(दिया है)} \ \mathrm{AD} & =\mathrm{AD}\quad \text {(उभयनिष्ठ)} \ \angle \mathrm{ADB} & =\angle \mathrm{ADC}=90^{\circ}\quad \text {(दिया है)} \end{aligned} $$

इसलिए, $\quad \quad \triangle \mathrm{ABD} \cong \triangle \mathrm{ACD}\quad \text { (ASA नियम)}$ इसलिए, $\quad \quad \mathrm{AB}=\mathrm{AC}\quad \text {(सर्वांगसम त्रिभुजों की संगत भागे)}$

$\triangle \mathrm{ABC}$ एक समद्विबाहु त्रिभुज है।

उदाहरण 5: $\mathrm{E}$ और $\mathrm{F}$ क्रमशः $\triangle \mathrm{ABC}$ के बराबर भुजाओं $\mathrm{AB}$ और $\mathrm{AC}$ के मध्य-बिंदु हैं (देखिए आकृति 7.28)। दिखाइए कि $\mathrm{BF}=\mathrm{CE}$।

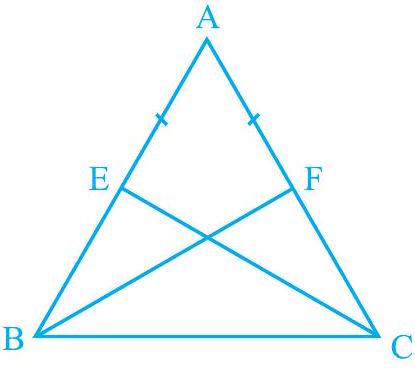
आकृति 7.28

हल: $\triangle \mathrm{ABF}$ और $\triangle \mathrm{ACE}$ में,

$$ \begin{aligned} & \mathrm{AB}=\mathrm{AC}\quad \text {दिया है} \\ & \angle \mathrm{A}=\angle \mathrm{A}\quad \text {उभयनिष्ठ} \\ & \mathrm{AF}=\mathrm{AE} \quad \text { (बराबर भुजाओं के आधे) } \end{aligned} $$ इसलिए,$\quad \quad \Delta \mathrm{ABF} \cong \Delta \mathrm{ACE} \quad(\mathrm{SAS} \text { नियम })$ अतः, $\quad \mathrm{BF}=\mathrm{CE}\quad \text {(CPCT)}$

उदाहरण 6: एक समद्विबाहु त्रिभुज $\mathrm{ABC}$ में जहाँ $\mathrm{AB}=\mathrm{AC}, \mathrm{D}$ और $\mathrm{E}$ बिंदु $\mathrm{BC}$ पर इस प्रकार हैं कि $B E=C D$ (देखिए आकृति 7.29)। दिखाइए कि $A D=A E$।

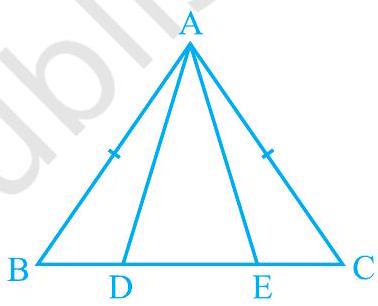
आकृति 7.29

हल: $\triangle \mathrm{ABD}$ और $\triangle \mathrm{ACE}$ में,

$$ \begin{aligned} \mathrm{AB} & =\mathrm{AC}\quad \text {(दिया गया है)} \quad (1)\\ \angle \mathrm{B} & =\angle \mathrm{C} \end{aligned} \text {(बराबर भुजाओं के सम्मुख कोण)}\quad (2) $$

साथ ही, $\quad \mathrm{BE}=\mathrm{CD}$

इसलिए, $\quad \mathrm{BE}-\mathrm{DE}=\mathrm{CD}-\mathrm{DE}$

अर्थात्, $\quad \mathrm{BD}=\mathrm{CE}\quad(3)$

इसलिए, $\quad \Delta \mathrm{ABD} \cong \triangle \mathrm{ACE}$ ((1), (2), (3) और SAS नियम का प्रयोग करते हुए)।

इससे प्राप्त होता है $\quad \mathrm{AD}=\mathrm{AE}$ $\quad(\mathrm{CPCT})$

7.5 त्रिभुजों की सर्वांगसमता के कुछ और मानदंड

आपने इस अध्याय में पहले देखा है कि एक त्रिभुज के तीन कोणों का दूसरे त्रिभुज के तीन कोणों के बराबर होना, दोनों त्रिभुजों की सर्वांगसमता के लिए पर्याप्त नहीं है। आप सोच रहे होंगे कि क्या एक त्रिभुज की तीन भुजाओं का दूसरे त्रिभुज की तीन भुजाओं के बराबर होना, दोनों त्रिभुजों की सर्वांगसमता के लिए पर्याप्त है। आपने पिछली कक्षाओं में यह सत्यापित किया है कि यह वास्तव में सत्य है।

निश्चित होने के लिए, 4 सेमी, 3.5 सेमी और 4.5 सेमी भुजाओं वाले दो त्रिभुज बनाएं (देखें आकृति 7.35)। उन्हें काटकर एक-दूसरे पर रखें। आप क्या प्रेक्षित करते हैं? वे एक-दूसरे को पूरी तरह ढक लेते हैं, यदि बराबर भुजाओं को एक-दूसरे पर रखा जाए। इसलिए, त्रिभुज सर्वांगसम हैं।

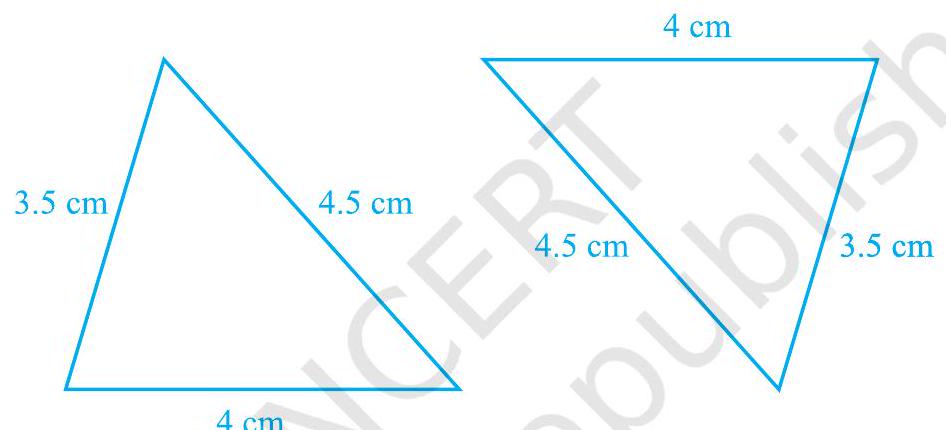
आकृति 7.35

इस क्रियाकलाप को कुछ और त्रिभुजों के साथ दोहराएँ। हम एक और सर्वांगसमता नियम पर पहुँचते हैं।

प्रमेय 7.4 (SSS सर्वांगसमता नियम) : यदि एक त्रिभुज की तीन भुजाएँ दूसरे त्रिभुज की तीन भुजाओं के बराबर हैं, तो दोनों त्रिभुज सर्वांगसम होते हैं।

इस प्रमेय को एक उपयुक्त रचना का उपयोग करके सिद्ध किया जा सकता है।

आपने पहले ही देखा है कि SAS सर्वांगसमता नियम में, बराबर कोणों का युग्म उन संगत बराबर भुजाओं के बीच का सम्मिलित कोण होना चाहिए और यदि ऐसा नहीं है, तो दोनों त्रिभुज सर्वांगसम नहीं हो सकते।

इस क्रियाकलाप को करें:

दो समकोण त्रिभुज बनाएँ जिनकी कर्ण 5 सेमी और एक भुजा 4 सेमी हो (देखें आकृति 7.36)।

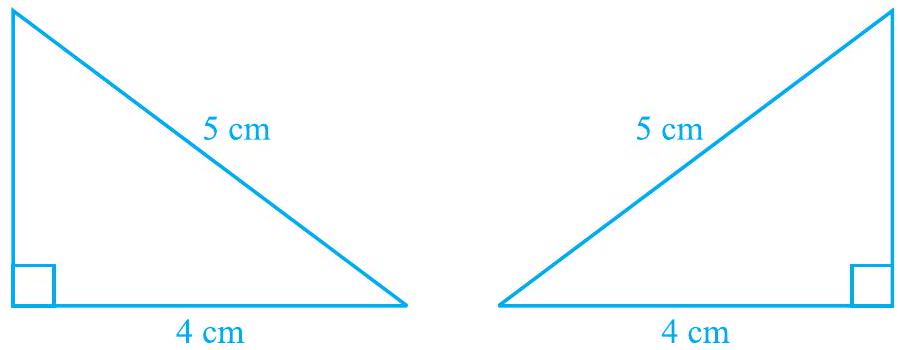
आकृति 7.36

इन्हें काटें और एक त्रिभुज को दूसरे के ऊपर इस प्रकार रखें कि बराबर भुजाएँ एक-दूसरे के ऊपर आ जाएँ। आवश्यकता हो तो त्रिभुजों को घुमाएँ। आप क्या देखते हैं?

दोनों त्रिभुज एक-दूसरे को पूरी तरह ढक लेते हैं और इसलिए वे सर्वांगसम हैं। इस क्रियाकलाप को अन्य समकोण त्रिभुजों के युग्मों के साथ दोहराएँ। आप क्या देखते हैं?

आप पाएँगे कि दो समकोण त्रिभुज तब सर्वांगसम होते हैं जब एक युग्म भुजाएँ और कर्ण बराबर हों। आपने इसे पिछली कक्षाओं में सत्यापित किया है। ध्यान दें कि, इस स्थिति में समकोण सम्मिलित कोण नहीं है।

इसलिए, आप निम्नलिखित सर्वांगसमता नियम पर पहुँचते हैं:

प्रमेय 7.5 (RHS सर्वांगसमता नियम) : यदि दो समकोण त्रिभुजों में एक त्रिभुज के कर्ण और एक भुजा, दूसरे त्रिभुज के कर्ण और एक भुजा के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं।

ध्यान दें कि RHS का अर्थ है समकोण - कर्ण - भुजा।

अब हम कुछ उदाहरण लेते हैं।

उदाहरण 7 : $\mathrm{AB}$ एक रेखाखंड है। $\mathrm{P}$ और $\mathrm{Q}$ बिंदु $\mathrm{AB}$ के विपरीत ओर इस प्रकार स्थित हैं कि प्रत्येक बिंदु A और B से समान दूरी पर है (देखिए आकृति 7.37)। दिखाइए कि रेखा PQ, $\mathrm{AB}$ का लंब समद्विभाजक है।

हल : आपको दिया गया है कि $\mathrm{PA}=\mathrm{PB}$ और $\mathrm{QA}=\mathrm{QB}$ और आपको यह दिखाना है कि $\mathrm{PQ} \perp \mathrm{AB}$ और $\mathrm{PQ}$, $\mathrm{AB}$ को समद्विभाजित करती है। मान लीजिए $\mathrm{PQ}$, $\mathrm{AB}$ को $\mathrm{C}$ पर काटती है।
क्या आप इस आकृति में दो सर्वांगसम त्रिभुज सोच सकते हैं?
आइए $\Delta$ PAQ और $\Delta$ PBQ लें।

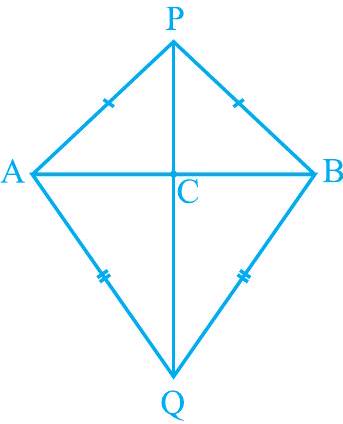
आकृति 7.37

इन त्रिभुजों में,

$\mathrm{AP}=\mathrm{BP}$ { (दिया गया है) }

$\mathrm{AQ}=\mathrm{BQ}$ {(दिया गया है)}

$\mathrm{PQ}=\mathrm{PQ}$ { (उभयनिष्ठ) }

इसलिए, $\triangle \mathrm{PAQ} \cong \triangle \mathrm{PBQ}$ { (SSS नियम) }

अतः, $\angle \mathrm{APQ}=\angle \mathrm{BPQ}$ { (CPCT) }

अब हम त्रिभुज PAC और त्रिभुज PBC पर विचार करते हैं।

$ You have : \mathrm{AP} =\mathrm{BP} (Given)$

$ \angle \mathrm{APC} =\angle \mathrm{BPC}(\angle \mathrm{APQ}=\angle \mathrm{BPQ} $ { (proved above) }

$ \mathrm{PC} =\mathrm{PC} { (Common) } $

So, $ \Delta \mathrm{PAC} \cong \Delta \mathrm{PBC}$ (SAS rule)

Therefore,$ \mathrm{AC} =\mathrm{BC} (\mathrm{CPCT})(1) $

and $ \angle \mathrm{ACP} =\angle \mathrm{BCP} (\mathrm{CPCT})$

$ \begin{array}{lrll} \text{ Also, } & \angle \mathrm{ACP}+\angle \mathrm{BCP} & =180^{\circ} & \text { (Linear pair) } \\ \text { So, } & 2 \angle \mathrm{ACP} & =180^{\circ} & \\ \text { 0r } & \angle \mathrm{ACP}& =90^{\circ} & (2)\\ \end{array} $

From (1) and (2), you can easily conclude that PQ is the perpendicular bisector of AB.

[Note that, without showing the congruence of $\triangle \mathrm{PAQ}$ and $\triangle \mathrm{PBQ}$, you cannot show that $\Delta \mathrm{PAC} \cong \Delta \mathrm{PBC}$ even though $\mathrm{AP}=\mathrm{BP}\quad \text {(Given)}$]

$\mathrm{PC}=\mathrm{PC} \quad \text {(Given)}$

and $\quad \angle \mathrm{PAC}=\angle \mathrm{PBC}$ (Angles opposite to equal sides in $\triangle \mathrm{APB})$

It is because these results give us SSA rule which is not always valid or true for congruence of triangles. Also the angle is not included between the equal pairs of sides.]

आइए कुछ और उदाहरण लेते हैं।

उदाहरण 8 : $\mathrm{P}$ एक बिंदु है जो दो रेखाओं $l$ और $m$ से समान दूरी पर है जो बिंदु A पर प्रतिच्छेद करती हैं (देखिए आकृति 7.38)। दिखाइए कि रेखा AP उनके बीच के कोण को समद्विभाजित करती है।

हल : आपको दिया गया है कि रेखाएँ $l$ और $m$ एक-दूसरे को A पर प्रतिच्छेद करती हैं। मान लीजिए PB $\perp l$, $\mathrm{PC} \perp m$। यह दिया गया है कि $\mathrm{PB}=\mathrm{PC}$।

आपको यह दि�ाना है कि $\angle \mathrm{PAB}=\angle \mathrm{PAC}$।

आइए हम $\Delta \mathrm{PAB}$ और $\triangle \mathrm{PAC}$ पर विचार करें। इन दो त्रिभुजों में,

$$ \begin{aligned} \mathrm{PB} & =\mathrm{PC}\quad \text {(दिया है)} \ \angle \mathrm{PBA} & =\angle \mathrm{PCA}=90^{\circ}\quad \text {(दिया है)} \ \mathrm{PA} & =\mathrm{PA}\quad \text {(उभयनिष्ठ)} \end{aligned} $$

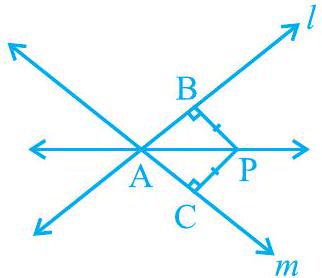
आकृति 7.38

इसलिए, $\quad \triangle \mathrm{PAB} \cong \triangle \mathrm{PAC}\quad \text {(RHS नियम)}$

इसलिए, $\quad \angle \mathrm{PAB}=\angle \mathrm{PAC}\quad \text {(CPCT)}$

ध्यान दें कि यह परिणाम अभ्यास 7.1 के प्रश्न 5 में सिद्ध किए गए परिणाम का व्युत्क्रम है।

7.6 सारांश

इस अध्याय में, आपने निम्नलिखित बिंदुओं का अध्ययन किया है :

1. दो आकृतियाँ सर्वांगसम होती हैं, यदि वे एक ही आकार की और एक ही आकार की हों।

2. समान त्रिज्या वाले दो वृत्त सर्वांगसम होते हैं।

3. समान भुजाओं वाले दो वर्ग सर्वांगसम होते हैं।

4. यदि दो त्रिभुज $\mathrm{ABC}$ और $\mathrm{PQR}$ अनुरूपता $\mathrm{A} \leftrightarrow \mathrm{P}$, $\mathrm{B} \leftrightarrow \mathrm{Q}$ और $\mathrm{C} \leftrightarrow \mathrm{R}$ के अंतर्गत सर्वांगसम हैं, तो प्रतीकात्मक रूप से इसे $\Delta \mathrm{ABC} \cong \Delta \mathrm{PQR}$ के रूप में व्यक्त किया जाता है।

5. यदि एक त्रिभुज की दो भुजाएँ और सम्मिलित कोण दूसरे त्रिभुज की दो भुजाओं और सम्मिलित कोण के बराबर हैं, तो दोनों त्रिभुज सर्वांगसम होते हैं (SAS सर्वांगसमता नियम)।

6. यदि एक त्रिभुज के दो कोण और सम्मिलित भुजा दूसरे त्रिभुज के दो कोणों और सम्मिलित भुजा के बराबर हैं, तो दोनों त्रिभुज सर्वांगसम होते हैं (ASA सर्वांगसमता नियम)।

7. यदि एक त्रिभुज के दो कोण और एक भुजा दूसरे त्रिभुज के दो कोणों और संगत भुजा के बराबर हैं, तो दोनों त्रिभुज सर्वांगसम होते हैं (AAS सर्वांगसमता नियम)।

8. त्रिभुज की बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।

9. त्रिभुज के बराबर कोणों के सम्मुख भुजाएँ बराबर होती हैं।

10. समबाहु त्रिभुज का प्रत्येक कोण $60^{\circ}$ का होता है।

11. यदि एक त्रिभुज की तीन भुजाएँ दूसरे त्रिभुज की तीन भुजाओं के बराबर हैं, तो दोनों त्रिभुज सर्वांगसम होते हैं (SSS सर्वांगसमता नियम)।

12. यदि दो समकोण त्रिभुजों में, एक त्रिभुज का कर्ण और एक भुजा दूसरे त्रिभुज के कर्ण और एक भुजा के बराबर हैं, तो दोनों त्रिभुज सर्वांगसम होते हैं (RHS सर्वांगसमता नियम)।