6.1 परिचय

अध्याय 5 में आपने अध्ययन किया है कि एक रेखा खींचने के लिए न्यूनतम दो बिंदुओं की आवश्यकता होती है। आपने कुछ अभिगृहितों का भी अध्ययन किया है और इन अभिगृहितों की सहायता से आपने कुछ अन्य कथनों को सिद्ध किया है। इस अध्याय में आप उन कोणों के गुणों का अध्ययन करेंगे जो बनते हैं जब दो रेखाएं एक-दूसरे को काटती हैं, और साथ ही उन कोणों के गुणों का भी अध्ययन करेंगे जो बनते हैं जब एक रेखा दो या अधिक समांतर रेखाओं को विभिन्न बिंदुओं पर काटती है। आगे आप इन गुणों का उपयोग कुछ कथनों को निगमनात्मक तर्क द्वारा सिद्ध करने में करेंगे (परिशिष्ट 1 देखें)। आपने इन कथनों को पहले की कक्षाओं में कुछ गतिविधियों के माध्यम से सत्यापित भी किया है।

अपने दैनिक जीवन में आप विभिन्न प्रकार के कोण देखते हैं जो समतल सतहों के किनारों के बीच बनते हैं। समतल सतहों का उपयोग करके इसी प्रकार के मॉडल बनाने के लिए आपको कोणों की गहरी जानकारी होनी चाहिए। उदाहरण के लिए, मान लीजिए आप स्कूल प्रदर्शनी में रखने के लिए एक झोपड़ी का मॉडल बांस की छड़ों से बनाना चाहते हैं। कल्पना कीजिए आप इसे कैसे बनाएंगे? आप कुछ छड़ों को एक-दूसरे के समांतर रखेंगे और कुछ छड़ों को तिरछी रखेंगे। जब भी कोई वास्तुकार किसी बहुमंजिली इमारत की योजना बनाती है, तो उसे विभिन्न कोणों पर प्रतिच्छेदी रेखाएं और समांतर रेखाएं खींचनी पड़ती हैं। क्या आपको लगता है कि इन रेखाओं और कोणों के गुणों की जानकारी के बिना वह इमारत की रूपरेखा बना सकती है?

विज्ञान में आप किरण आरेख बनाकर प्रकाश के गुणों का अध्ययन करते हैं। उदाहरण के लिए, जब प्रकाश एक माध्यम से दूसरे माध्यम में प्रवेश करता है तो उसके अपवर्तन गुण का अध्ययन करने के लिए आप प्रतिच्छेदी रेखाओं और समांतर रेखाओं के गुणों का प्रयोग करते हैं। जब किसी वस्तु पर दो या अधिक बल कार्य करते हैं, तो आप एक ऐसा आरेख बनाते हैं जिसमें बलों को निर्देशित रेखाखंडों द्वारा दर्शाया जाता है ताकि वस्तु पर बलों के संयुक्त प्रभाव का अध्ययन किया जा सके। उस समय आपको यह जानना होता है कि जब किरणें (या रेखाखंड) समांतर हों या एक-दूसरे को प्रतिच्छेद करें तो कोणों के बीच क्या संबंध होता है। किसी मीनार की ऊँचाई ज्ञात करने या किसी प्रकाश स्तम्भ से जहाज़ की दूरी निकालने के लिए क्षैतिज रेखा और दृष्टि रेखा के बीच बने कोण को जानना आवश्यक होता है। और भी अनेक उदाहरण दिए जा सकते हैं जहाँ रेखाओं और कोणों का प्रयोग होता है। ज्यामिति के आगे के अध्यायों में आप इन रेखाओं और कोणों के गुणों का प्रयोग करते हुए और भी उपयोगी गुणों का निष्कर्ष निकालेंगे।

आइए पहले पिछली कक्षाओं में सीखी गई रेखाओं और कोणों से संबंधित पदों और परिभाषाओं की पुनरावृत्ति करें।

6.2 आधारभूत पद और परिभाषाएँ

याद कीजिए कि एक रेखा का वह भाग (या अंश) जिसके दो अंत बिंदु हों, रेखाखंड कहलाता है और एक रेखा का वह भाग जिसका एक अंत बिंदु हो, किरण कहलाती है। ध्यान दीजिए कि रेखाखंड $A B$ को $\overline{\mathrm{AB}}$ द्वारा दर्शाया जाता है, और इसकी लंबाई को $\mathrm{AB}}$ द्वारा दर्शाया जाता है। किरण $\mathrm{AB}$ को $\overrightarrow{\mathrm{AB}}$ द्वारा दर्शाया जाता है, और एक रेखा को $\overleftrightarrow{A B}$ द्वारा दर्शाया जाता है। हालांकि, हम इन प्रतीकों का प्रयोग नहीं करेंगे, और रेखाखंड $\mathrm{AB}$, किरण $\mathrm{AB}$, लंबाई $\mathrm{AB}$ और रेखा $\mathrm{AB}$ को एक ही प्रतीक, $\mathrm{AB}$ द्वारा दर्शाएंगे। अर्थ संदर्भ से स्पष्ट हो जाएगा। कभी-कभी रेखाओं को दर्शाने के लिए छोटे अक्षर $l, m, n$, आदि का प्रयोग किया जाएगा।

यदि तीन या अधिक बिंदु एक ही रेखा पर स्थित हों, तो उन्हें संरेख बिंदु कहा जाता है; अन्यथा उन्हें असंरेख बिंदु कहा जाता है।

याद कीजिए कि जब दो किरणें एक ही अंत बिंदु से प्रारंभ होती हैं, तो एक कोण बनता है। कोण बनाने वाली किरणों को कोण की भुजाएँ कहा जाता है और अंत बिंदु को कोण का शीर्ष कहा जाता है। आपने पिछली कक्षाओं में विभिन्न प्रकार के कोणों का अध्ययन किया है, जैसे न्यून कोण, समकोण, अधिक कोण, सरल कोण और पुनः कोण (देखिए चित्र 6.1)।

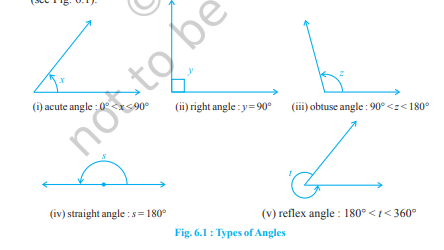
चित्र 6.1 : कोणों के प्रकार

एक न्यून कोण $0^{\circ}$ और $90^{\circ}$ के बीच मापा जाता है, जबकि एक समकोण ठीक $90^{\circ}$ के बराबर होता है। एक कोण जो $90^{\circ}$ से अधिक हो परंतु $180^{\circ}$ से कम हो, अधिक कोण कहलाता है। साथ ही, याद रखिए कि एक सरल कोण $180^{\circ}$ के बराबर होता है। एक कोण जो $180^{\circ}$ से अधिक हो परंतु $360^{\circ}$ से कम हो, पुनःकोण कहलाता है। इसके अतिरिक्त, दो कोण जिनका योग $90^{\circ}$ हो, संपूरक कोण कहलाते हैं, और दो कोण जिनका योग $180^{\circ}$ हो, पूरक कोण कहलाते हैं।

आपने पिछली कक्षाओं में संलग्न कोणों के बारे में भी पढ़ा है (देखिए चित्र 6.2)। दो कोण संलग्न होते हैं, यदि उनमें एक उभयनिष्ठ शीर्ष, एक उभयनिष्ठ भुजा हो और उनकी असामान्य भुजाएँ उभयनिष्ठ भुजा के विभिन्न पार्श्वों पर हों। चित्र 6.2 में, $\angle \mathrm{ABD}$ और $\angle \mathrm{DBC}$ संलग्न कोण हैं। किरण $\mathrm{BD}$ उनकी उभयनिष्ठ भुजा है और बिंदु $\mathrm{B}$ उनका उभयनिष्ठ शीर्ष है। किरण $\mathrm{BA}$ और किरण $\mathrm{BC}$ असामान्य भुजाएँ हैं। इसके अतिरिक्त, जब दो कोण संलग्न होते हैं, तब उनका योग सदैव उस कोण के बराबर होता है जो दो असामान्य

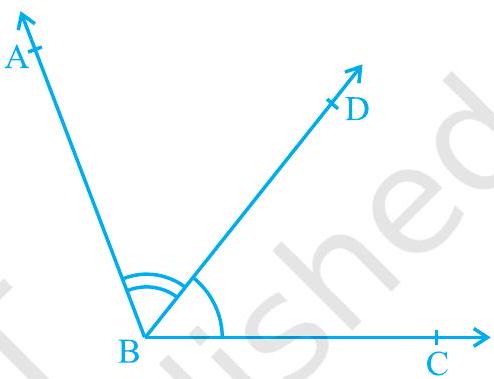
चित्र 6.2 : संलग्न कोण भुजाओं द्वारा बनाया जाता है। इसलिए, हम लिख सकते हैं

$\angle \mathrm{ABC}=\angle \mathrm{ABD}+\angle \mathrm{DBC} .$

ध्यान दें कि $\angle \mathrm{ABC}$ और $\angle \mathrm{ABD}$ संलग्न कोण नहीं हैं। क्यों? क्योंकि उनकी असमान भुजाएँ $\mathrm{BD}$ और $\mathrm{BC}$ उभयनिष्ठ भुजा BA के एक ही ओर स्थित हैं।

यदि चित्र 6.2 में असमान भुजाएँ $\mathrm{BA}$ और $\mathrm{BC}$ एक रेखा बनाती हैं, तो यह चित्र 6.3 जैसा दिखेगा। इस स्थिति में, $\angle \mathrm{ABD}$ और $\angle \mathrm{DBC}$ को रैखिक कोण युग्म कहा जाता है।

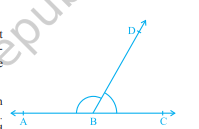
चित्र 6.3 : रैखिक कोण युग्म

आपको शायद याद हो कि जब दो रेखाएँ, मान लीजिए $\mathrm{AB}$ और $\mathrm{CD}$, एक-दूसरे को बिंदु $\mathrm{O}$ पर काटती हैं (चित्र 6.4 देखें), तो उभयनिष्ठ विपरीत कोण बनते हैं। उभयनिष्ठ विपरीत कोणों के दो युग्म होते हैं।

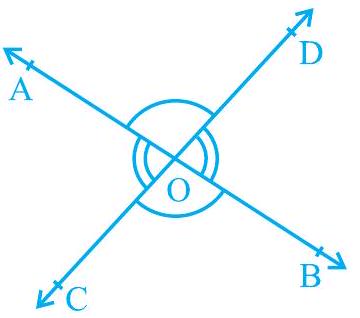
चित्र 6.4 : उभयनिष्ठ विपरीत कोण

एक युग्म $\angle \mathrm{AOD}$ और $\angle \mathrm{BOC}$ है। क्या आप दूसरा युग्म खोज सकते हैं?

6.3 प्रतिच्छेदी रेखाएँ और अप्रतिच्छेदी रेखाएँ

कागज़ पर दो भिन्न रेखाएँ PQ और RS खींचिए। आप देखेंगे कि आप उन्हें चित्र 6.5 (i) और चित्र 6.5 (ii) में दिखाए गए दो भिन्न तरीकों से खींच सकते हैं।

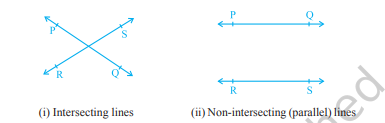
चित्र 6.5 : दो रेखाओं को खींचने के विभिन्न तरीके

रेखा की अवधारणा को याद कीजिए, कि यह दोनों दिशाओं में अनिश्चित रूप से फैली होती है। चित्र 6.5 (i) में रेखाएँ PQ और RS प्रतिच्छेदी रेखाएँ हैं और चित्र 6.5 (ii) में समांतर रेखाएँ हैं। ध्यान दीजिए कि इन समांतर रेखाओं पर विभिन्न बिंदुओं पर उभयनिष्ठ लंबों की लंबाइयाँ समान होती हैं। इस समान लंबाई को दो समांतर रेखाओं के बीच की दूरी कहा जाता है।

6.4 कोणों के युग्म

अनुभाग 6.2 में, आपने कोणों के कुछ युग्मों जैसे पूरक कोण, संपूरक कोण, संलग्न कोण, रेखीय कोण युग्म आदि की परिभाषाएँ सीखी हैं। क्या आप इन कोणों के बीच कुछ संबंध सोच सकते हैं? अब, आइए ज्ञात करें कि जब कोई किरण एक रेखा पर खड़ी होती है तब बने कोणों के बीच क्या संबंध होता है। एक ऐसा चित्र बनाइए जिसमें एक किरण एक रेखा पर खड़ी हो जैसा कि चित्र 6.6 में दिखाया गया है। रेखा का नाम AB और किरण का नाम OC रखिए। बिंदु O पर कौन-से कोण बनते हैं? वे हैं ∠AOC, ∠BOC और ∠AOB।

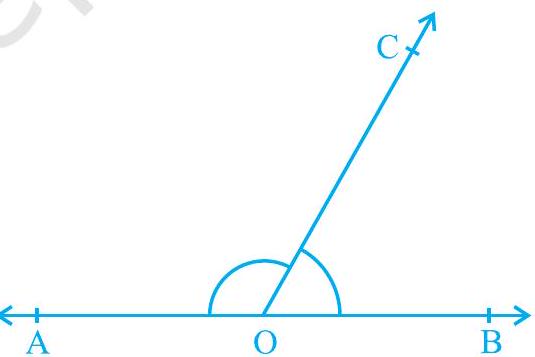
चित्र 6.6 : रेखीय कोण युग्म बिंदु

क्या हम ∠AOC + ∠BOC = ∠AOB लिख सकते हैं? (1)

हाँ! (क्यों? अनुभाग 6.2 में संलग्न कोणों को देखें)

∠AOB का माप क्या है? यह 180° है। (क्यों?) (2)

(1) और (2) से, क्या आप कह सकते हैं कि ∠AOC + ∠BOC = 180°? हाँ! (क्यों?)

उपरोक्त चर्चा से हम निम्नलिखित अभिगृहित को कह सकते हैं:

अभिगृहित 6.1: यदि एक किरण एक रेखा पर खड़ी हो, तो बने हुए दो संलग्न कोणों का योग 180° होता है।

याद कीजिए कि जब दो संलग्न कोणों का योग 180° होता है, तो उन्हें रेखीय युग्म कोण कहा जाता है।

अभिगृहित 6.1 में यह दिया गया है कि ‘एक किरण एक रेखा पर खड़ी है’। इस ‘दिए गए’ से हमने निष्कर्ष निकाला है कि ‘बने हुए दो संलग्न कोणों का योग 180° है’। क्या हम अभिगृहित 6.1 को उल्टे क्रम में लिख सकते हैं? यानी, अभिगृहित 6.1 के ‘निष्कर्ष’ को ‘दिया गया’ और ‘दिए गए’ को ‘निष्कर्ष’ बना दें। तो यह इस प्रकार होगा:

(A) यदि दो संलग्न कोणों का योग 180° है, तो एक किरण एक रेखा पर खड़ी होती है (अर्थात्, असामान्य भुजाएँ एक रेखा बनाती हैं)।

अब आप देख सकते हैं कि अभिगृहित 6.1 और कथन (A) एक दूसरे के उल्टे हैं। हम प्रत्येक को दूसरे का व्युत्क्रम कहते हैं। हम नहीं जानते कि कथन (A) सत्य है या नहीं। आइए जाँच करें। चित्र 6.7 में दिखाए गए अनुसार विभिन्न मापों के संलग्न कोण बनाएँ। प्रत्येक स्थिति में एक असामान्य भुजा के साथ रूलर रखें। क्या दूसरी असामान्य भुजा भी रूलर के साथ लाइन में है?

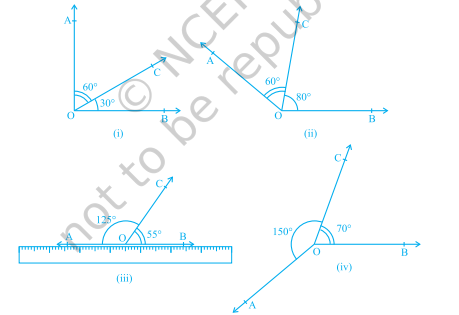
चित्र 6.7 : भिन्न मापों वाले संलग्न कोण

आप पाएंगे कि केवल चित्र 6.7 (iii) में, दोनों असामान्य भुजाएँ रूलर के साथ हैं, अर्थात् बिंदु $\mathrm{A}, \mathrm{O}$ और $\mathrm{B}$ एक ही रेखा पर हैं और किरण $\mathrm{OC}$ इस पर खड़ी है। यह भी देखें कि $\angle \mathrm{AOC}+\angle \mathrm{COB}=125^{\circ}+55^{\circ}=180^{\circ}$। इससे आप निष्कर्ष निकाल सकते हैं कि कथन (A) सत्य है। इसलिए, आप इसे निम्नलिखित रूप में एक अभिगृहित के रूप में कह सकते हैं:

अभिगृहित 6.2 : यदि दो संलग्न कोणों का योग $180^{\circ}$ हो, तो कोणों की असामान्य भुजाएँ एक रेखा बनाती हैं।

स्पष्ट कारणों से, उपरोक्त दोनों अभिगृहितों को एक साथ रैखिक युग्म अभिगृहित कहा जाता है।

आइए अब उस स्थिति की जाँच करें जब दो रेखाएँ एक-दूसरे को काटती हैं।

पिछली कक्षाओं से याद करें, कि जब दो रेखाएँ काटती हैं, तो उभयनिष्ठ कोण बराबर होते हैं। आइए अब इस परिणाम को सिद्ध करें। सिद्ध करने के तत्वों के लिए परिशिष्ट 1 देखें, और नीचे दिए गए सिद्धांत को पढ़ते समय उन्हें ध्यान में रखें।

प्रमेय 6.1 : यदि दो रेखाएँ एक-दूसरे को काटती हैं, तो उभयनिष्ठ कोण बराबर होते हैं।

प्रमाण : उपरोक्त कथन में यह दिया गया है कि ‘दो रेखाएँ एक-दूसरे को काटती हैं’। इसलिए, मान लें कि $\mathrm{AB}$ और $\mathrm{CD}$ दो रेखाएँ हैं जो चित्र 6.8 में दिखाए अनुसार बिंदु $\mathrm{O}$ पर काटती हैं। वे उभयनिष्ठ कोणों के दो युग्म बनाती हैं, अर्थात्

(i) $\angle \mathrm{AOC}$ और $\angle \mathrm{BOD}$ (ii) $\angle \mathrm{AOD}$ और $\angle \mathrm{BOC}$.

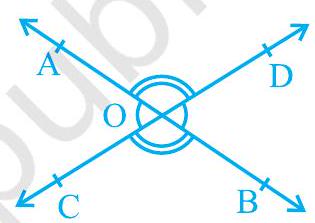
चित्र 6.8 : शीर्षाभिमुख कोण

हमें यह सिद्ध करना है कि $\angle \mathrm{AOC}=\angle \mathrm{BOD}$

और $\angle \mathrm{AOD}=\angle \mathrm{BOC}$.

अब, किरण $\mathrm{OA}$ रेखा $\mathrm{CD}$ पर स्थित है।

इसलिए, $\angle \mathrm{AOC}+\angle \mathrm{AOD}=180^{\circ}$

क्या हम $\angle \mathrm{AOD}+\angle \mathrm{BOD}=180^{\circ}$ लिख सकते हैं? हाँ! (क्यों?)

(1) और (2) से, हम लिख सकते हैं

$$\angle \mathrm{AOC}+\angle \mathrm{AOD}=\angle \mathrm{AOD}+\angle \mathrm{BOD}$$

इसका तात्पर्य है कि $\angle \mathrm{AOC}=\angle \mathrm{BOD} \quad$ (देखें खण्ड 5.2, अभिगृहित 3)

इसी प्रकार, यह सिद्ध किया जा सकता है कि $\angle \mathrm{AOD}=\angle \mathrm{BOC}$

अब, आइए रैखिक युग्म अभिगृहित और प्रमेय 6.1 पर आधारित कुछ उदाहरण करें।

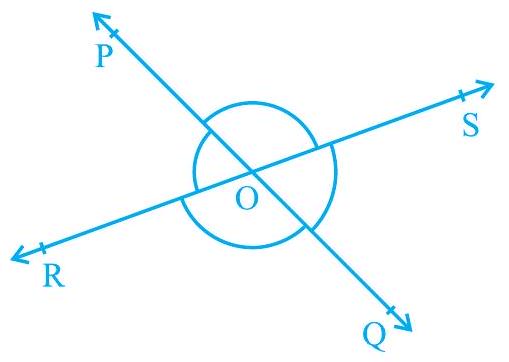
उदाहरण 1 : चित्र 6.9 में, रेखाएँ PQ और RS बिंदु $O$ पर परस्पर प्रतिच्छेद करती हैं। यदि $\angle \mathrm{POR}: \angle \mathrm{ROQ}=5: 7$, तो सभी कोण ज्ञात कीजिए।

हल : $\angle \mathrm{POR}+\angle \mathrm{ROQ}=180^{\circ}$

(रैखिक युग्म कोण)

परंतु $\angle \mathrm{POR}: \angle \mathrm{ROQ}=5: 7$ (दिया है)

इसलिए, $\quad \angle \mathrm{POR}=\frac{5}{12} \times 180^{\circ}=75^{\circ}$

इसी प्रकार, $\quad \angle \mathrm{ROQ}=\frac{7}{12} \times 180^{\circ}=105^{\circ}$

अब, $$\begin{aligned} & \angle \mathrm{POS}=\angle \mathrm{ROQ}=105^{\circ} \\ & \angle \mathrm{SOQ}=\angle \mathrm{POR}=75^{\circ} \end{aligned}$$

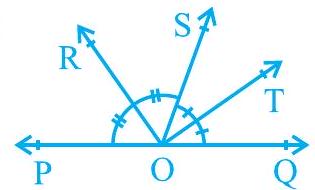
उदाहरण 2 : चित्र 6.10 में, किरण OS रेखा POQ पर स्थित है। किरण OR और किरण OT क्रमशः $\angle \mathrm{POS}$ और $\angle \mathrm{SOQ}$ के कोण समद्विभाजक हैं। यदि $\angle \mathrm{POS}=x$ है, तो $\angle \mathrm{ROT}$ ज्ञात कीजिए।

हल : किरण OS रेखा POQ पर स्थित है।

इसलिए,

$\angle \mathrm{POS}+\angle \mathrm{SOQ}=180^{\circ}$

लेकिन,

$$\angle \mathrm{POS}=x$$

इसलिए, अतः,

$x+\angle \mathrm{SOQ} =180^{\circ} \\ \angle \mathrm{SOQ} =180^{\circ}-x$

अब, किरण OR, $\angle \mathrm{POS}$ का समद्विभाजक है, इसलिए,

चित्र 6.10

$$ \begin{aligned} \angle \mathrm{ROS} & =\frac{1}{2} \times \angle \mathrm{POS} \\ & =\frac{1}{2} \times x=\frac{x}{2} \end{aligned} $$

इसी प्रकार,

$$ \begin{aligned} \angle \mathrm{SOT} & =\frac{1}{2} \times \angle \mathrm{SOQ} \ & =\frac{1}{2} \times\left(180^{\circ}-x\right) \ & =90^{\circ}-\frac{x}{2} \end{aligned} $$

अब,

$$ \begin{aligned} \angle \mathrm{ROT} & =\angle \mathrm{ROS}+\angle \mathrm{SOT} \ & =\frac{x}{2}+90^{\circ}-\frac{x}{2} \ & =90^{\circ} \end{aligned} $$

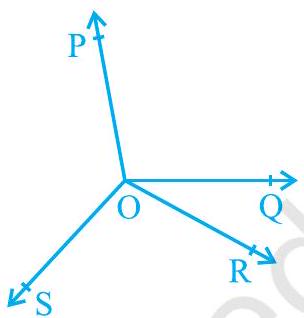
उदाहरण 3 : चित्र 6.11 में, OP, OQ, OR और OS चार किरणें हैं। सिद्ध कीजिए कि $\angle \mathrm{POQ}+\angle \mathrm{QOR}+\angle \mathrm{SOR}+$ $\angle \mathrm{POS}=360^{\circ}$।

हल : चित्र 6.11 में, आपको किसी भी किरण $\mathrm{OP}, \mathrm{OQ}$, OR या OS को पीछे की ओर किसी बिंदु तक बढ़ाना होगा। आइए किरण $\mathrm{OQ}$ को पीछे की ओर बिंदु $\mathrm{T}$ तक बढ़ाएं ताकि TOQ एक रेखा हो (चित्र 6.12 देखें)।

चित्र 6.11

अब, किरण OP रेखा TOQ पर खड़ी है।

इसलिए,

$\angle \mathrm{TOP}+\angle \mathrm{POQ}=180^{\circ}$

(रैखिक युग्म अभिगृहीत)

इसी प्रकार, किरण OS रेखा TOQ पर खड़ी है।

इसलिए,

$\angle \mathrm{TOS}+\angle \mathrm{SOQ}=180^{\circ}$

$\angle \mathrm{SOQ}=\angle \mathrm{SOR}+\angle \mathrm{QOR}$

अतः, (2) बन जाता है

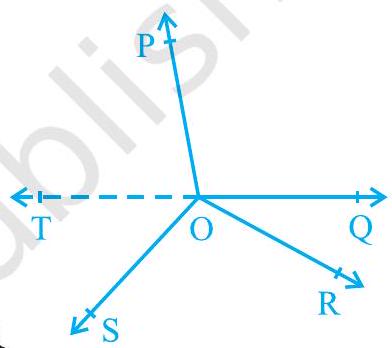
आकृति 6.12

$$ \begin{equation*} \angle \mathrm{TOS}+\angle \mathrm{SOR}+\angle \mathrm{QOR}=180^{\circ} \tag{3} \end{equation*} $$

अब, (1) और (3) को जोड़ने पर, आपको प्राप्त होता है

$$ \begin{equation*} \angle \mathrm{TOP}+\angle \mathrm{POQ}+\angle \mathrm{TOS}+\angle \mathrm{SOR}+\angle \mathrm{QOR}=360^{\circ} \tag{4} \end{equation*} $$

लेकिन

$\angle \mathrm{TOP}+\angle \mathrm{TOS}=\angle \mathrm{POS}$

इसलिए, (4) बन जाता है

$$\angle \mathrm{POQ}+\angle \mathrm{QOR}+\angle \mathrm{SOR}+\angle \mathrm{POS}=360^{\circ}$$

6.5 एक ही रेखा के समांतर रेखाएँ

यदि दो रेखाएँ एक ही रेखा के समांतर हों, तो क्या वे एक-दूसरे के समांतर होंगी? आइए इसकी जाँच करें। आकृति 6.18 देखिए जिसमें रेखा $m ||$ रेखा $l$ और रेखा $n ||$ रेखा $l$ है। आइए रेखा $t$ खींचें जो रेखाओं $l$, $m$ और $n$ के लिए एक अनुवर्ती रेखा है। यह दिया गया है कि रेखा $m ||$ रेखा $l$ और रेखा $n ||$ रेखा $l$ है।

इसलिए, $\angle 1=\angle 2$ और $\angle 1=\angle 3$

(संगत कोणों का अभिगृहित) इसलिए, $\quad \angle 2=\angle 3$ (क्यों?)

लेकिन $\angle 2$ और $\angle 3$ संगत कोण हैं और वे समान हैं।

इसलिए, आप कह सकते हैं कि

$\text { रेखा } m || \text { रेखा } n$

(संगत कोणों के अभिगृहित का व्युत्क्रम)

इस परिणाम को निम्नलिखित प्रमेय के रूप में कहा जा सकता है:

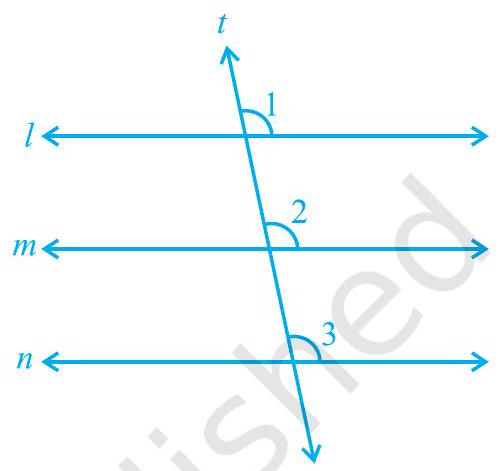
आकृति 6.18

प्रमेय 6.6 : जिन रेखाओं की समान रेखा के साथ समानांतरता हो, वे आपस में भी समानांतर होती हैं।

टिप्पणी: उपरोक्त गुणधर्म को दो से अधिक रेखाओं पर भी विस्तारित किया जा सकता है।

अब, आइए समानांतर रेखाओं से संबंधित कुछ उदाहरणों को हल करें।

उदाहरण 4 : चित्र 6.19 में, यदि $\mathrm{PQ} || \mathrm{RS}, \angle \mathrm{MXQ}=135^{\circ}$ और $\angle \mathrm{MYR}=40^{\circ}$ है, तो $\angle \mathrm{XMY}$ ज्ञात कीजिए।

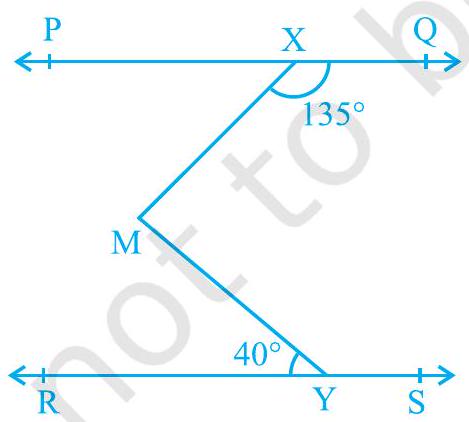
चित्र 6.19

हल : यहाँ, हमें बिंदु $\mathrm{M}$ से होकर जाने वाली एक रेखा AB खींचनी है जो रेखा $\mathrm{PQ}$ के समानांतर हो, जैसा कि चित्र 6.20 में दिखाया गया है। अब, $A B ||P Q$ और $P Q || R S$ है।

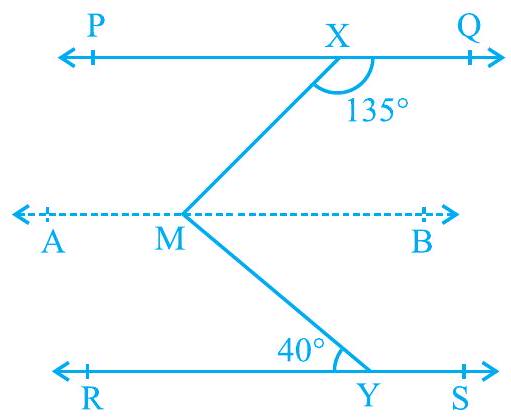
चित्र 6.20

इसलिए, $\quad \quad \quad$$\mathrm{AB} || \mathrm{RS}$ $\quad$(क्यों?)

अब, $\quad \quad \quad$$\angle \mathrm{QXM}+\angle \mathrm{XMB}=180^{\circ}$

$\quad \quad \quad$(AB ||PQ, अंतः कोण जो एक ही तिर्यक रेखा XM के एक ही ओर स्थित हैं)

परंतु $\quad \quad \quad$$\angle \mathrm{QXM}=135^{\circ}$

इसलिए, $\quad \quad \quad$$135^{\circ}+\angle \mathrm{XMB}=180^{\circ}$

अतः, $\quad \quad \quad$$\angle \mathrm{XMB}=45^{\circ}$ $\quad \quad \quad$(1)

अब,$\quad \quad \quad$$\angle \mathrm{BMY}=\angle \mathrm{MYR}$$\quad$(AB $||$ RS, एकान्तर कोण)

इसलिए,$\quad \quad \quad$$\angle \mathrm{BMY}=40^{\circ}$ $\quad \quad \quad$(2)

(1) और (2) को जोड़ने पर, आपको मिलता है

$\quad \quad \quad$$\angle \mathrm{XMB}+\angle \mathrm{BMY}=45^{\circ}+40^{\circ}$

अर्थात्, $\quad \quad \quad$ $\angle XMY=85^{\circ}$

उदाहरण 5 : यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार काटती है कि एक युग्म के संगत कोणों के समद्विभाजक समानांतर हों, तो सिद्ध कीजिए कि वे दोनों रेखाएँ समानांतर हैं।

हल : चित्र 6.21 में, एक तिर्यक रेखा AD दो रेखाओं PQ और RS को बिंदु B और $\mathrm{C}$ पर क्रमशः काटती है। किरण $\mathrm{BE}$ कोण $\angle \mathrm{ABQ}$ का समद्विभाजक है और किरण $\mathrm{CG}$ कोण $\angle \mathrm{BCS}$ का समद्विभाजक है; और $\mathrm{BE} || \mathrm{CG}$।

हमें सिद्ध करना है कि $\mathrm{PQ} || \mathrm{RS}$।

यह दिया गया है कि किरण $\mathrm{BE}$ कोण $\angle \mathrm{ABQ}$ का समद्विभाजक है।

इसलिए, $\quad \angle \mathrm{ABE}=\frac{1}{2} \angle \mathrm{ABQ}$$\quad \quad \quad$(1)

इसी प्रकार, किरण $\mathrm{CG}$ कोण $\angle \mathrm{BCS}$ का समद्विभाजक है।

इसलिए, $\quad \angle \mathrm{BCG}=\frac{1}{2} \angle \mathrm{BCS}$$\quad \quad \quad$(2)

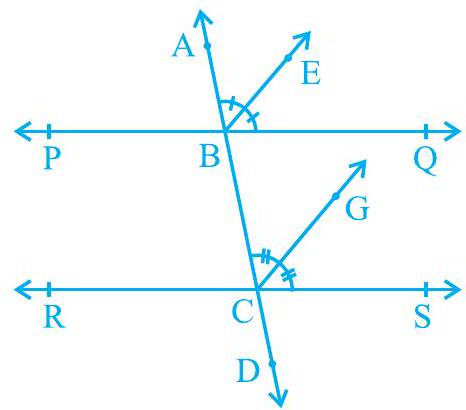
चित्र 6.21

लेकिन $\mathrm{BE} || \mathrm{CG}$ और $\mathrm{AD}$ तिर्यक रेखा है।

इसलिए, $\quad \angle \mathrm{ABE}=\angle \mathrm{BCG}$ (समान कोण अभिगृहीत)$\quad \quad \quad$(3)

(1) और (2) को (3) में प्रतिस्थापित करने पर, आपको प्राप्त होता है

$$\frac{1}{2} \angle \mathrm{ABQ}=\frac{1}{2} \angle \mathrm{BCS}$$

अर्थात्, $\quad$$\angle \mathrm{ABQ}=\angle \mathrm{BCS}$

लेकिन, ये कोण AD द्वारा PQ और RS के साथ बनाए गए संगत कोण हैं; और बराबर हैं।

इसलिए,

PQ $||$ RS

(संगत कोण अभिगृहीत का व्युत्क्रम)

उदाहरण 6 : आकृति 6.22 में, $\mathrm{AB} || \mathrm{CD}$ और $\mathrm{CD} || \mathrm{EF}$। साथ ही $\mathrm{EA} \perp \mathrm{AB}$। यदि $\angle \mathrm{BEF}=55^{\circ}$ हो, तो $x, y$ और $z$ के मान ज्ञात कीजिए।

हल : $y+55^{\circ}=180^{\circ}$

(एक ही तिर्यक ED के एक ही ओर आंतरिक कोण)

इसलिए, $\quad$ $y=180^{\circ}-55^{\circ}=125^{\circ}$

पुनः $\quad \quad \quad$$x=y$

$\quad \quad$( $\mathrm{AB} || \mathrm{CD}$, संगत कोण अभिगृहीत)

इसलिए $\quad \quad$$x=125^{\circ}$

अब, चूँकि $\mathrm{AB} || \mathrm{CD}$ और $\mathrm{CD} || \mathrm{EF}$, इसलिए, $\mathrm{AB} || \mathrm{EF}$।

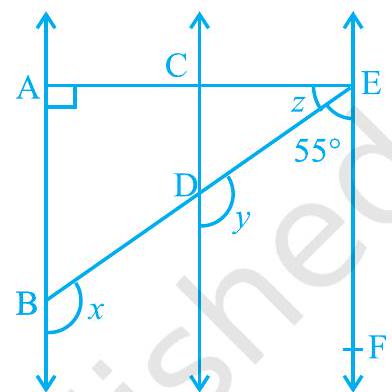
आकृति 6.22

इसलिए, $\quad \quad$$\angle \mathrm{EAB}+\angle \mathrm{FEA}=180^{\circ}$(तिर्यक EA के एक ही ओर आंतरिक कोण)

इसलिए, $\quad$$90^{\circ}+z+55^{\circ}=180^{\circ}$

जिससे $\quad$$z=35^{\circ}$

6.6 सारांश

इस अध्याय में आपने निम्नलिखित बिंदुओं का अध्ययन किया है:

1. यदि एक किरण एक रेखा पर खड़ी हो, तो बनने वाले दो संलग्न कोणों का योग $180^{\circ}$ होता है और इसका विलोम भी सत्य है। इस गुणधर्म को रैखिक युग्म अभिगृहीत कहा जाता है।

2. यदि दो रेखाएं एक-दूसरे को प्रतिच्छेद करती हैं, तो उभयपृष्ठ कोण समान होते हैं।

3. रेखाएं जो किसी दी गई रेखा के समानांतर होती हैं, वे एक-दूसरे के भी समानांतर होती हैं।