5.1 परिचय

‘ज्यामिति’ शब्द ग्रीक शब्दों ‘जियो’, जिसका अर्थ है ‘पृथ्वी’, और ‘मेट्रिन’, जिसका अर्थ है ‘मापना’, से आया है। ज्यामिति की उत्पत्ति भूमि को मापने की आवश्यकता से प्रतीत होती है। गणित की इस शाखा को प्रत्येक प्राचीन सभ्यता में विभिन्न रूपों में अध्ययन किया गया, चाहे वह मिस्र, बेबीलोन, चीन, भारत, ग्रीस, इंकास आदि हो। इन सभ्यताओं के लोगों को कई व्यावहारिक समस्याओं का सामना करना पड़ा जिन्हें विभिन्न तरीकों से ज्यामिति के विकास की आवश्यकता थी।

उदाहरण के लिए, जब भी नील नदी उफनती थी, तो यह विभिन्न भूमि स्वामियों की सटेकड़ी खेतों की सीमाओं को मिटा देती थी। ऐसी बाढ़ के बाद इन सीमाओं को फिर से खींचना पड़ता था। इस उद्देश्य के लिए, मिस्रियों ने सरल क्षेत्रफलों की गणना करने और सरल रचनाएँ करने के लिए कई ज्यामितीय तकनीकों और नियमों का विकास किया। ज्यामिति का ज्ञान उनके द्वारा अन्नागारों के आयतनों की गणना करने और नहरों और पिरामिडों के निर्माण के लिए भी प्रयोग किया गया। उन्हें एक छिन्न पिरामिड का आयतन ज्ञात करने का सही सूत्र भी पता था (देखें चित्र 5.1)। आप जानते हैं कि एक पिरामिड एक ठोस आकृति होती है, जिसका आधार एक त्रिभुज, या वर्ग, या कोई अन्य बहुभुज होता है, और इसकी भुजाओं के तल ऊपर की ओर एक बिंदु पर मिलने वाले त्रिभुज होते हैं।

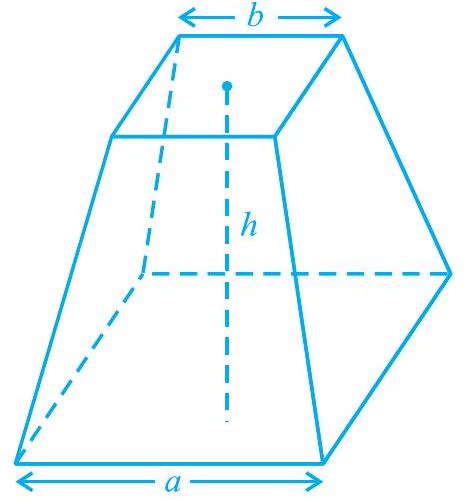
चित्र 5.1 : एक छिन्न पिरामिड

भारतीय उपमहाद्वीप में हड़प्पा और मोहनजो-दारो आदि की खुदाइयों से पता चलता है कि सिंधु घाटी सभ्यता (लगभग 3000 ईसा पूर्व) ने ज्यामिति का व्यापक उपयोग किया था। यह एक अत्यंत संगठित समाज था। शहर अत्यधिक विकसित और बहुत अच्छी तरह से नियोजित थे। उदाहरण के लिए, सड़कें एक-दूसरे के समानांतर थीं और एक भूमिगत नाली प्रणाली थी। घरों में विभिन्न प्रकार के कई कमरे थे। यह दर्शाता है कि नगरवासी मापन और व्यावहारिक अंकगणित में निपुण थे। निर्माण के लिए प्रयुक्त ईंटें भट्ठी में पकाई जाती थीं और ईंटों की लंबाई : चौड़ाई : मोटाई का अनुपात 4:2:1 पाया गया।

प्राचीन भारत में, शुल्बसूत्र ($800 \mathrm{BCE}$ से $500 \mathrm{BCE}$) ज्यामितीय रचनाओं की मैनुअल थे। वैदिक काल की ज्यामिति वेदियों (या वेदियों) और वैदिक संस्कारों के प्रदर्शन के लिए अग्नि स्थलों की रचना से उत्पन्न हुई। पवित्र अग्नियों का स्थान स्पष्ट रूप से निर्धारित निर्देशों के अनुसार उनके आकार और क्षेत्रफल के बारे में होना था, यदि वे प्रभावी उपकरण बनने थे। घरेलू अनुष्ठानों के लिए वर्गाकार और वृत्ताकार वेदियों का उपयोग किया जाता था, जबकि सार्वजनिक पूजा के लिए आयतों, त्रिभुजों और समलंबों के संयोजन वाले आकारों की वेदियों की आवश्यकता होती थी। श्रीयंत्र (अथर्ववेद में दिया गया) नौ आंतरिक समद्विबाहु त्रिभुजों से बना है। ये त्रिभुज इस प्रकार व्यवस्थित हैं कि वे 43 सहायक त्रिभुज उत्पन्न करते हैं। यद्यपि वेदियों की रचना के लिए सटीक ज्यामितीय विधियों का उपयोग किया गया था, उनके पीछे के सिद्धांतों पर चर्चा नहीं की गई थी।

ये उदाहरण दिखाते हैं कि ज्यामिति को दुनिया के हर कोने में विकसित और लागू किया जा रहा था। लेकिन यह सब एक अव्यवस्थित तरीके से हो रहा था। प्राचीन दुनिया में ज्यामिति के इन विकासों के बारे में दिलचस्प बात यह है कि इन्हें एक पीढ़ी से दूसरी पीढ़ी तक या तो मौखिक रूप से, ताड़ के पत्तों पर लिखकर, या अन्य तरीकों से आगे बढ़ाया गया। साथ ही, हम पाते हैं कि कुछ सभ्यताओं जैसे बेबीलोन में ज्यामिति एक अत्यंत व्यावहारिक विषय बनी रही, जैसा कि भारत और रोम में था। मिस्रियों द्वारा विकसित ज्यामिति मुख्यतः परिणामों के कथनों पर आधारित थी। प्रक्रिया के कोई सामान्य नियम नहीं थे। वास्तव में, बेबीलोनियों और मिस्रियों ने ज्यामिति का उपयोग ज्यादातर व्यावहारिक उद्देश्यों के लिए किया और इसे एक व्यवस्थित विज्ञान के रूप में विकसित करने के लिए बहुत कम किया। लेकिन ग्रीस जैसी सभ्यताओं में जोर इस बात पर था कि कुछ रचनाएँ क्यों काम करती हैं, इसके पीछे का तर्क क्या है। यूनानी उन कथनों की सत्यता स्थापित करने में रुचि रखते थे जिन्हें उन्होंने निगमनात्मक तर्क का उपयोग करके खोजा था (देखिए परिशिष्ट 1)।
एक ग्रीक गणितज्ञ, थेल्स को पहला ज्ञात प्रमाण देने का श्रेय दिया जाता है। यह प्रमाण इस कथन का था कि एक वृत्त को उसका व्यास समद्विभाजित करता है (अर्थात् दो बराबर भागों में काटता है)। थेल्स के सबसे प्रसिद्ध शिष्यों में से एक पाइथागोरस (५७२ ई.पू.) था, जिसके बारे में आपने सुना होगा। पाइथागोरस और उसके समूह ने कई ज्यामितीय गुणधर्मों की खोज की और ज्यामिति के सिद्धांत को काफी हद तक विकसित किया। यह प्रक्रिया लगभग ३०० ई.पू. तक चलती रही। उस समय मिस्र के अलेक्जेंड्रिया में गणित के अध्यापक यूक्लिड ने सभी ज्ञात कार्यों को एकत्र किया और अपने प्रसिद्ध ग्रंथ में व्यवस्थित किया।

थेल्स (640 ईसा पूर्व - 546 ईसा पूर्व)

इस अध्याय में, हम यूक्लिड की ज्यामिति के प्रति दृष्टिकोण पर चर्चा करेंगे और इसे आज की ज्यामिति से जोड़ने का प्रयास करेंगे।

यूक्लिड (325 ईसा पूर्व - 265 ईसा पूर्व)

चित्र 5.3

5.2 यूक्लिड की परिभाषाएँ, अभिगृहित और अभिधारणाएँ

यूक्लिड के समय के ग्रीक गणितज्ञ ज्यामिति को उस संसार का एक अमूर्त मॉडल मानते थे जिसमें वे रहते थे। बिंदु, रेखा, समतल (या सतह) आदि की धारणाएँ उन चीज़ों से ली गई थीं जो उनके चारों ओर दिखती थीं। अंतरिक्ष और उसमें स्थित ठोस वस्तुओं के अध्ययन से, ठोस वस्तु की एक अमूर्त ज्यामितीय धारणा विकसित की गई। एक ठोस का आकार, आकार, स्थान होता है, और इसे एक स्थान से दूसरे स्थान पर ले जाया जा सकता है। इसकी सीमाओं को सतहें कहा जाता है। वे अंतरिक्ष के एक भाग को दूसरे से अलग करती हैं, और इनकी कोई मोटाई नहीं होती। सतहों की सीमाएँ वक्र या सीधी रेखाएँ होती हैं। ये रेखाएँ बिंदुओं पर समाप्त होती हैं।

विचारें ठोस से बिंदुओं तक के तीन चरणों को (ठोस-सतह-रेखाएँ-बिंदु)। प्रत्येक चरण में हम एक विस्तार खो देते हैं, जिसे आयाम भी कहा जाता है। इसलिए, एक ठोस के तीन आयाम होते हैं, एक सतह के दो, एक रेखा का एक और एक बिंदु का कोई नहीं। यूक्लिड ने इन कथनों को परिभाषाओं के रूप में संक्षेपित किया। उसने अपने प्रस्तुति की शुरुआत ‘एलिमेंट्स’ की पुस्तक 1 में 23 परिभाषाओं की सूची बनाकर की। उनमें से कुछ नीचे दी गई हैं:

1. एक बिंदु वह है जिसका कोई भाग नहीं है।
2. एक रेखा बिना चौड़ाई की लंबाई है।
3. एक रेखा के अंत बिंदु होते हैं।
4. एक सीधी रेखा वह रेखा है जो स्वयं पर स्थित बिंदुओं के साथ समान रूप से लेटी हो।
5. एक सतह वह है जिसमें केवल लंबाई और चौड़ाई होती है।
6. एक सतह के किनारे रेखाएँ होती हैं।
7. एक समतलीय सतह वह सतह है जो स्वयं पर स्थित सीधी रेखाओं के साथ समान रूप से लेटी हो।

यदि आप इन परिभाषाओं का ध्यानपूर्वक अध्ययन करें, तो आप पाएंगे कि कुछ पद जैसे भाग, चौड़ाई, लंबाई, समान रूप से, आदि को और स्पष्ट रूप से समझाया जाना चाहिए। उदाहरण के लिए, बिंदु की उसकी परिभाषा पर विचार करें। इस परिभाषा में, ‘एक भाग’ को परिभाषित करने की आवश्यकता है। मान लीजिए यदि आप ‘एक भाग’ को वह परिभाषित करते हैं जो ‘क्षेत्र’ घेरता है, तो फिर ‘एक क्षेत्र’ को परिभाषित करने की आवश्यकता है। इसलिए, एक चीज़ को परिभाषित करने के लिए, आपको कई अन्य चीज़ों को परिभाषित करना पड़ता है, और आपको परिभाषाओं की एक लंबी श्रृंखला मिल सकती है जिसका कोई अंत नहीं है। ऐसे कारणों से, गणितज्ञ कुछ ज्यामितीय पदों को अपरिभाषित छोड़ने पर सहमत होते हैं। हालांकि, हमें बिंदु की ज्यामितीय अवधारणा के लिए एक सहज भावना अवश्य होती है, जो उपरोक्त ‘परिभाषा’ से कहीं अधिक है। इसलिए, हम एक बिंदु को एक बिंदु के रूप में प्रस्तुत करते हैं, यद्यपि एक बिंदु की कुछ विमाएँ होती हैं।

उपरोक्त परिभाषा 2 में एक समान समस्या उत्पन्न होती है, क्योंकि इसमें चौड़ाई और लंबाई का उल्लेख है, जिनमें से किसी को भी परिभाषित नहीं किया गया है। इस कारण से, किसी भी अध्ययन पाठ्यक्रम को विकसित करते समय कुछ पदों को अपरिभाषित रखा जाता है। इसलिए, ज्यामिति में, हम एक बिंदु, एक रेखा और एक समतल (यूक्लिड के शब्दों में एक समतल सतह) को अपरिभाषित पदों के रूप में लेते हैं। केवल इतना है कि हम उन्हें सहज रूप से प्रस्तुत कर सकते हैं, या ‘भौतिक मॉडलों’ की सहायता से उनकी व्याख्या कर सकते हैं।

अपनी परिभाषाओं से प्रारंभ करते हुए, यूक्लिड ने कुछ ऐसे गुणधर्मों को मान लिया जिन्हें सिद्ध नहीं किया जाना था। ये मान्यताएँ वास्तव में ‘स्पष्ट सार्वभौमिक सत्य’ हैं। उसने इन्हें दो प्रकारों में विभाजित किया: सिद्धांत (axioms) और अभिधान (postulates)। उसने ‘अभिधान’ शब्द उन मान्यताओं के लिए प्रयोग किया जो केवल ज्यामिति से संबंधित थीं। सामान्य धारणाएँ (जिन्हें प्रायः सिद्धांत कहा जाता है), दूसरी ओर, ऐसी मान्यताएँ थीं जो संपूर्ण गणित में प्रयुक्त होती थीं और विशेष रूप से ज्यामिति से जुड़ी नहीं होती थीं। सिद्धांतों और अभिधानों के विवरण के लिए, कृपया परिशिष्ट 1 देखें। यूक्लिड के कुछ सिद्धांत, उसके क्रमानुसार नहीं, नीचे दिए गए हैं:

(1) जो वस्तुएँ किसी एक ही वस्तु के समान हैं, वे एक-दूसरे के समान होती हैं।

(2) यदि समान वस्तुओं में समान वस्तुएँ जोड़ी जाएँ, तो सम्पूर्ण समान होते हैं।

(3) यदि समान वस्तुओं से समान वस्तुएँ घटाई जाएँ, तो शेष समान होते हैं।

(4) जो वस्तुएँ एक-दूसरे के संपाती (coincide) हैं, वे एक-दूसरे के समान होती हैं।

(5) सम्पूर्ण, अंश से बड़ा होता है।

(6) जो वस्तुएँ किसी एक ही वस्तु की दुगुनी हैं, वे एक-दूसरे के समान होती हैं।

(7) जो वस्तुएँ किसी एक ही वस्तु की आधी हैं, वे एक-दूसरे के समान होती हैं।

ये ‘सामान्य धारणाएँ’ किसी प्रकार की मात्राओं को संदर्भित करती हैं। पहली सामान्य धारणा को समतलीय आकृतियों पर लागू किया जा सकता है। उदाहरण के लिए, यदि किसी त्रिभुज का क्षेत्रफल आयत के क्षेत्रफल के समान है और आयत का क्षेत्रफल वर्ग के क्षेत्रफल के समान है, तो त्रिभुज का क्षेत्रफल भी वर्ग के क्षेत्रफल के समान है।

समान प्रकार की मात्राओं की तुलना और जोड़ की जा सकती है, परंतु भिन्न प्रकार की मात्राओं की तुलना नहीं की जा सकती। उदाहरण के लिए, एक रेखा की तुलना एक आयत से नहीं की जा सकती, न ही एक कोण की तुलना एक पंचभुज से की जा सकती है।

ऊपर दिया गया चौथा अभिगृहित यह कहता प्रतीत होता है कि यदि दो वस्तुएँ समान हैं (अर्थात् वे एक ही हैं), तो वे बराबर हैं। दूसरे शब्दों में, हर वस्तु स्वयं के बराबर है। यह अध्यारोपण के सिद्धांत का औचित्य प्रदान करता है। अभिगृहित (5) हमें ‘बड़ा है’ की परिभाषा देता है। उदाहरण के लिए, यदि कोई मात्रा B दूसरी मात्रा A का एक भाग है, तो A को B और किसी तीसरी मात्रा C के योग के रूप में लिखा जा सकता है। प्रतीकात्मक रूप से, A > B का अर्थ है कि कोई ऐसी $\mathrm{C}$ है जिससे $\mathrm{A}=\mathrm{B}+\mathrm{C}$।

अब आइए यूक्लिड के पाँच अभिगृहितों पर चर्चा करें। वे इस प्रकार हैं :

अभिगृहित 1 : किसी एक बिन्दु से किसी अन्य बिन्दु तक एक सीधी रेखा खींची जा सकती है।

ध्यान दें कि यह अभिगृहित हमें बताता है कि कम-से-कम एक सीधी रेखा दो भिन्न बिन्दुओं से होकर गुजरती है, परंतु यह नहीं कहता कि ऐसी एक से अधिक रेखाएँ नहीं हो सकतीं। फिर भी, अपने कार्य में यूक्लिड ने बार-बार यह मान लिया है, बिना उल्लेख किए, कि दो भिन्न बिन्दुओं को मिलाने वाली एक अद्वितीय रेखा होती है। हम इस परिणाम को निम्नलिखित रूप में एक अभिगृहित के रूप में प्रस्तुत करते हैं :

अभिगृहित 5.1 : दो भिन्न बिन्दुओं को दी गई हो, एक अद्वितीय रेखा होती है जो उनसे होकर गुजरती है।

$P$ से गुज़रने वाली कितनी रेखाएँ $Q$ से भी गुज़रती हैं (देखिए चित्र 5.4)? केवल एक, वह है रेखा $PQ$। $Q$ से गुज़रने वाली कितनी रेखाएँ $P$ से भी गुज़रती हैं? केवल एक, वह है रेखा PQ। इस प्रकार, उपरोक्त कथन आत्म-स्पष्ट है, और इसलिए इसे एक अभिगृहीत के रूप में लिया गया है।

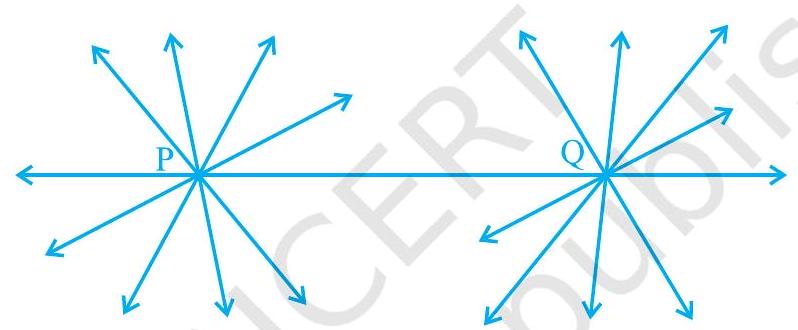
चित्र 5.4

अभिगृहीत 2 : एक समाप्त रेखा को अनिश्चित रूप से बढ़ाया जा सकता है।

ध्यान दें कि आजकल हम जिसे रेखाखंड कहते हैं, यूक्लिड उसे समाप्त रेखा कहता था। इसलिए आज के शब्दों में दूसरा अभिगृहीत कहता है कि एक रेखाखंड को किसी भी ओर बढ़ाकर एक रेखा बनाई जा सकती है (देखिए चित्र 5.5)।

चित्र 5.5

अभिगृहीत 3 : किसी भी केंद्र और किसी भी त्रिज्या के साथ एक वृत्त खींचा जा सकता है।

अभिगृहीत 4 : सभी समकोण एक-दूसरे के बराबर होते हैं।

अभिगृहीत 5 : यदि एक सीधी रेखा दो सीधी रेखाओं पर गिरती है और उसी ओर के अंतःकोणों का योग दो समकोणों से कम हो, तो वे दोनों सीधी रेखाएँ, यदि अनिश्चित रूप से बढ़ाई जाएँ, तो उसी ओर मिलती हैं जिस ओर कोणों का योग दो समकोणों से कम है।

उदाहरण के लिए, चित्र 5.6 में रेखा PQ रेखाओं AB और CD पर इस प्रकार पड़ती है कि PQ के बाईं ओर आंतरिक कोण 1 और 2 का योग 180° से कम है। इसलिए, रेखाएँ AB और CD अंततः PQ के बाईं ओर प्रतिच्छेद करेंगी।

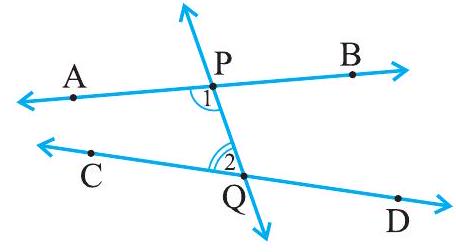
चित्र 5.6

पाँचों अभिगृहितों पर एक नज़र डालने से आपको यह स्पष्ट होता है कि अभिगृहित 5 अन्य किसी भी अभिगृहित की तुलना में कहीं अधिक जटिल है। दूसरी ओर, अभिगृहित 1 से 4 इतने सरल और स्वतः सिद्ध हैं कि इन्हें ‘स्वतः स्पष्ट सत्य’ माना जाता है। फिर भी, इन्हें सिद्ध करना संभव नहीं है। इसलिए, इन कथनों को बिना किसी प्रमाण के स्वीकार कर लिया जाता है (देखिए परिशिष्ट 1)। अपनी जटिलता के कारण, पाँचवें अभिगृहित को अगले खंड में अधिक विस्तार से देखा जाएगा।

आजकल ‘अभिगृहित’ और ‘स्वयंसिद्ध’ ऐसे शब्द हैं जिन्हें परस्पर विनिमय रूप से और एक ही अर्थ में प्रयोग किया जाता है। ‘अभिगृहित’ वास्तव में एक क्रिया है। जब हम कहते हैं “आइए अभिगृहित करें”, तो हमारा तात्पर्य होता है “आइए ब्रह्मांड में प्रेक्षित घटना के आधार पर कोई कथन बनाएँ”। इसकी सत्यता/वैधता बाद में जाँची जाती है। यदि यह सत्य हो, तो इसे ‘अभिगृहित’ के रूप में स्वीकार कर लिया जाता है।

एक नियमों (axioms) की प्रणाली को सुसंगत (consistent) कहा जाता है (देखिए परिशिष्ट 1), यदि इन नियमों से ऐसा कोई कथन निकालना असंभव है जो किसी नियम या पहले सिद्ध किए गए कथन का विरोधाभास करता हो। इसलिए, जब भी कोई नियमों की प्रणाली दी जाती है, यह सुनिश्चित करना आवश्यक होता है कि वह प्रणाली सुसंगत है।

यूक्लिड ने अपने अभिग्रह (postulates) और नियम (axioms) कहे, फिर उनका उपयोग करके अन्य परिणामों को सिद्ध किया। फिर इन परिणामों का उपयोग करके उसने कुछ और परिणामों को तर्कसंगत विचार (deductive reasoning) लगाकर सिद्ध किया। जिन कथनों को सिद्ध किया गया उन्हें प्रस्ताव (propositions) या प्रमेय (theorems) कहा जाता है। यूक्लिड ने अपने नियमों, अभिग्रहों, परिभाषाओं और श्रृंखला में पहले सिद्ध किए गए प्रमेयों का उपयोग करते हुए 465 प्रस्तावों को एक तार्किक श्रृंखला में निकाला। ज्यामिति पर आने वाले अगले कुछ अध्यायों में आप इन नियमों का उपयोग कुछ प्रमेयों को सिद्ध करने में करेंगे।

अब आइए निम्न उदाहरणों में देखें कि यूक्लिड ने कुछ परिणामों को सिद्ध करने के लिए अपने नियमों और अभिग्रहों का उपयोग कैसे किया:

उदाहरण 1 : यदि $\mathrm{A}, \mathrm{B}$ और $\mathrm{C}$ एक रेखा पर तीन बिंदु हैं, और $\mathrm{B}$, $\mathrm{A}$ और $\mathrm{C}$ के बीच में स्थित है (देखिए चित्र 5.7), तो सिद्ध कीजिए कि $\mathrm{AB}+\mathrm{BC}=\mathrm{AC}$।

चित्र 5.7

हल : ऊपर दिए गए चित्र में, $\mathrm{AC}$, $\mathrm{AB}+\mathrm{BC}$ के संपाती (coincides) है।

साथ ही, यूक्लिड का सिद्धांत (4) कहता है कि जो चीज़ें एक-दूसरे के संपाती हैं, वे एक-दूसरे के बराबर होती हैं। इसलिए, इससे यह निष्कर्ष निकाला जा सकता है कि

$\mathrm{AB}+\mathrm{BC}=\mathrm{AC}$

ध्यान दें कि इस समाधान में यह मान लिया गया है कि दो बिंदुओं से गुज़रने वाली एक अद्वितीय रेखा होती है।

उदाहरण 2 : सिद्ध कीजिए कि किसी भी दी गई रेखाखंड पर एक समबाहु त्रिभुज बनाया जा सकता है।

समाधान : उपरोक्त कथन में, किसी भी लंबाई की एक रेखाखंड दी गई है, मान लीजिए AB [देखिए आकृति 5.8(i)]।

आकृति 5.8

यहाँ, आपको कुछ रचना करनी होगी। यूक्लिड के सिद्धांत 3 का उपयोग करके, आप बिंदु $A$ को केंद्र और $A B$ को त्रिज्या मानकर एक वृत्त खींच सकते हैं [देखिए आकृति 5.8(ii)]। इसी प्रकार, बिंदु $\mathrm{B}$ को केंद्र और $\mathrm{BA}$ को त्रिज्या मानकर एक अन्य वृत्त खींचिए। दोनों वृत्त एक बिंदु पर मिलते हैं, मान लीजिए $\mathrm{C}$। अब, रेखाखंड $\mathrm{AC}$ और $\mathrm{BC}$ खींचकर $\triangle \mathrm{ABC}$ बनाइए [देखिए आकृति 5.8 (iii)]।

इसलिए, आपको यह सिद्ध करना है कि यह त्रिभुज समबाहु है, अर्थात् $\mathrm{AB}=\mathrm{AC}=\mathrm{BC}$।

अब, $\quad \mathrm{AB}=\mathrm{AC}$, क्योंकि ये एक ही वृत्त की त्रिज्याएँ हैं

इसी प्रकार, $A B=B C \quad$ (एक ही वृत्त की त्रिज्याएँ)

इन दोनों तथ्यों और यूक्लिड के सिद्धांत से कि जो चीज़ें किसी एक ही चीज़ के बराबर हैं, वे एक-दूसरे के भी बराबर होती हैं, आप यह निष्कर्ष निकाल सकते हैं कि $\mathrm{AB}=\mathrm{BC}=\mathrm{AC}$।

इसलिए, $\triangle \mathrm{ABC}$ एक समबाहु त्रिभुज है।

ध्यान दें कि यहाँ यूक्लिड ने बिना कहीं उल्लेख किए यह मान लिया है कि A और B केंद्रों से खींचे गए दो वृत्त एक-दूसरे किसी बिंदु पर मिलेंगे।

अब हम एक प्रमेय सिद्ध करते हैं, जिसका उपयोग विभिन्न परिणामों में प्रायः किया जाता है:

प्रमेय 5.1: दो भिन्न रेखाओं का एक से अधिक बिंदु उभयनिष्ठ नहीं हो सकता।

प्रमाण: यहाँ हमें दो रेखाएँ $l$ और $m$ दी गई हैं। हमें यह सिद्ध करना है कि उनका उभयनिष्ठ केवल एक बिंदु है।

अभी के लिए मान लीजिए कि दोनों रेखाएँ दो भिन्न बिंदुओं, मान लीजिए $\mathrm{P}$ और $\mathrm{Q}$, पर प्रतिच्छेद करती हैं। इस प्रकार आपके पास दो रेखाएँ दो भिन्न बिंदुओं $\mathrm{P}$ और $\mathrm{Q}$ से होकर जाती हैं। पर यह अभिधारणा उस अभिगृहित के विरुद्ध जाती है कि दो भिन्न बिंदुओं से केवल एक ही रेखा गुजर सकती है। इसलिए वह अभिधारणा, जिससे हमने प्रारंभ किया था कि दो रेखाएँ दो भिन्न बिंदुओं से होकर जा सकती हैं, गलत है।

इससे हम क्या निष्कर्ष निकालते हैं? हम यह निष्कर्ष निकालने को विवश हैं कि दो भिन्न रेखाओं का एक से अधिक बिंदु उभयनिष्ठ नहीं हो सकता।

5.3 सारांश

इस अध्याय में आपने निम्नलिखित बिंदुओं का अध्ययन किया है:

1. यद्यपि यूक्लिड ने बिंदु, रेखा और समतल की परिभाषा दी, पर गणितज्ञों द्वारा ये परिभाषाएँ स्वीकार नहीं की जातीं। इसलिए इन पदों को अब अपरिभाषित माना जाता है।

2. अभिगृहित या अभिधारणाएँ ऐसी मान्यताएँ होती हैं जो स्पष्टतः सार्वभौमिक सत्य होती हैं। इन्हें सिद्ध नहीं किया जाता।

3. प्रमेय ऐसे कथन होते हैं जिन्हें परिभाषाओं, अभिगृहितों, पूर्व में सिद्ध किए गए कथनों और तर्कसंगत तर्क के प्रयोग से सिद्ध किया जाता है।

4. यूक्लिड के कुछ अभिगृहित इस प्रकार थे:

(1) वे चीज़ें जो एक ही चीज़ के बराबर हैं, एक-दूसरे के भी बराबर होती हैं।

(2) यदि बराबरों में बराबर जोड़े जाएँ, तो कुल बराबर होते हैं।

(3) यदि बराबरों से बराबर घटाए जाएँ, तो शेष बराबर होते हैं।

(4) वे चीज़ें जो एक-दूसरे के संपाती हैं, एक-दूसरे के बराबर होती हैं।

(5) पूर्ण भाग से बड़ा होता है।

(6) वे चीज़ें जो एक ही चीज़ के दुगुनी हैं, एक-दूसरे के बराबर होती हैं।

(7) वे चीज़ें जो एक ही चीज़ की आधी हैं, एक-दूसरे के बराबर होती हैं।

5. यूक्लिड की अभिधारणाएँ थीं :

अभिधारणा 1 : किसी एक बिंदु से किसी अन्य बिंदु तक एक सीधी रेखा खींची जा सकती है।

अभिधारणा 2 : एक सीमित रेखा को अनिश्चित रूप से बढ़ाया जा सकता है।

अभिधारणा 3 : किसी भी केंद्र और किसी भी त्रिज्या के साथ एक वृत्त खींचा जा सकता है।

अभिधारणा 4 : सभी समकोण एक-दूसरे के बराबर होते हैं।