3.1 परिचय

आप पहले ही सीख चुके हैं कि संख्या रेखा पर किसी बिंदु को कैसे स्थित किया जाता है। आप यह भी जानते हैं कि रेखा पर किसी बिंदु की स्थिति को कैसे वर्णित किया जाता है। ऐसे कई अन्य परिस्थितियाँ हैं, जिनमें किसी बिंदु को खोजने के लिए हमें उसकी स्थिति एक से अधिक रेखाओं के सापेक्ष वर्णित करनी पड़ती है। उदाहरण के लिए, निम्नलिखित परिस्थितियों पर विचार करें:

I. चित्र 3.1 में, एक मुख्य सड़क पूर्व-पश्चिम दिशा में चल रही है और सड़कें पश्चिम से पूर्व की ओर क्रमांकित हैं। साथ ही, प्रत्येक सड़क पर मकानों की संख्या अंकित है। यहाँ किसी मित्र के मकान को खोजने के लिए क्या केवल एक संदर्भ बिंदु जानना पर्याप्त है? उदाहरण के लिए, यदि हमें केवल यह पता है कि वह सड़क 2 पर रहती है, तो क्या हम उसके मकान को आसानी से खोज पाएँगे? जब तक हमें इसके बारे में दो जानकारियाँ नहीं मिलतीं, अर्थात् जिस सड़क पर यह स्थित है उसकी संख्या और मकान की संख्या, तब तक नहीं। यदि हम उस मकान तक पहुँचना चाहते हैं जो $2^{\text{वीं}}$ सड़क पर स्थित है और जिसकी संख्या 5 है, तो सबसे पहले हम $2^{\text{वीं}}$ सड़क की पहचान करेंगे और फिर उस पर संख्या 5 वाला मकान खोजेंगे। चित्र 3.1 में, H मकान की स्थिति दिखाता है। इसी प्रकार, P उस मकान की स्थिति दिखाता है जो सड़क

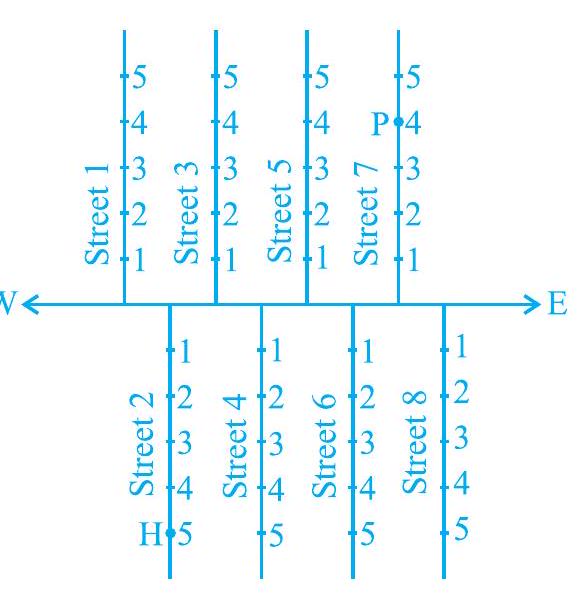
चित्र 3.1 संख्या 7 और मकान संख्या 4 से संबंधित है।

II. मान लीजिए आपने कागज़ की एक शीट पर एक बिंदि बनाया है [चित्र 3.2 (a)]। यदि हम आपसे पूछें कि कागज़ पर बिंदि की स्थिति क्या है, तो आप यह कैसे बताएँगे? शायद आप किसी इस तरह से कोशिश करेंगे: “बिंदि कागज़ के ऊपरी हिस्से में है”, या “यह कागज़ के बाएँ किनारे के पास है”, या “यह शीट के बाएँ ऊपरी कोने के बहुत पास है”। क्या इनमें से कोई भी कथन बिंदि की स्थिति को ठीक-ठीक निर्धारित करता है? नहीं! लेकिन, यदि आप कहें “बिंदि कागज़ के बाएँ किनारे से लगभग $5 \mathrm{~cm}$ दूर है”, तो यह कुछ अंदाज़ा देने में मदद करता है लेकिन फिर भी बिंदि की स्थिति को निर्धारित नहीं करता। थोड़ा-सा विचार करने पर आप यह कह सकेंगे कि बिंदि नीचे की रेखा से $9 \mathrm{~cm}$ ऊपर भी है। अब हमें ठीक-ठीक पता चल गया है कि बिंदि कहाँ है!

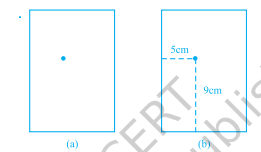
चित्र 3.2

इस उद्देश्य के लिए, हमने बिंदि की स्थिति को दो निश्चित रेखाओं—कागज़ के बाएँ किनारे और कागज़ की नीचे की रेखा—से उसकी दूरियाँ बताकर निर्धारित की है [चित्र 3.2 (b)]। दूसरे शब्दों में, बिंदि की स्थिति ज्ञात करने के लिए हमें दो स्वतंत्र जानकारियों की आवश्यकता होती है।

अब, निम्नलिखित कक्षाकक्षी गतिविधि ‘Seating Plan’ को करें।

गतिविधि 1 (बैठने की योजना): अपनी कक्षा में बैठने की योजना बनाएं, सभी डेस्कों को एक साथ मिलाकर। प्रत्येक डेस्क को एक वर्ग द्वारा दर्शाएं। प्रत्येक वर्ग में उस छात्र का नाम लिखें जो उस डेस्क पर बैठा है, जिसे वह वर्ग दर्शाता है। कक्षा में प्रत्येक छात्र की स्थिति को दो स्वतंत्र जानकारियों का उपयोग करके सटीक रूप से वर्णित किया जाता है:

(i) वह कॉलम जिसमें वह बैठता या बैठती है,

(ii) वह पंक्ति जिसमें वह बैठता या बैठती है।

यदि आप उस डेस्क पर बैठे हैं जो $5^{\text{वें}}$ कॉलम और $3^{\text{री}}$ पंक्ति में है (चित्र 3.3 में छायांकित वर्ग द्वारा दर्शाया गया), तो आपकी स्थिति को (5,3) लिखा जा सकता है, पहले कॉलम संख्या लिखकर और फिर पंक्ति संख्या लिखकर। क्या यह (3,5) के समान है? अपनी कक्षा के अन्य छात्रों के नाम और स्थितियाँ लिखें। उदाहरण के लिए, यदि सोनिया $4^{\text{वें}}$ कॉलम और $1^{\text{स्ट}}$ पंक्ति में बैठी है, तो $S(4,1)$ लिखें। शिक्षक की डेस्क आपकी बैठने की योजना का हिस्सा नहीं है। हम शिक्षक को केवल एक प्रेक्षक के रूप में मान रहे हैं।

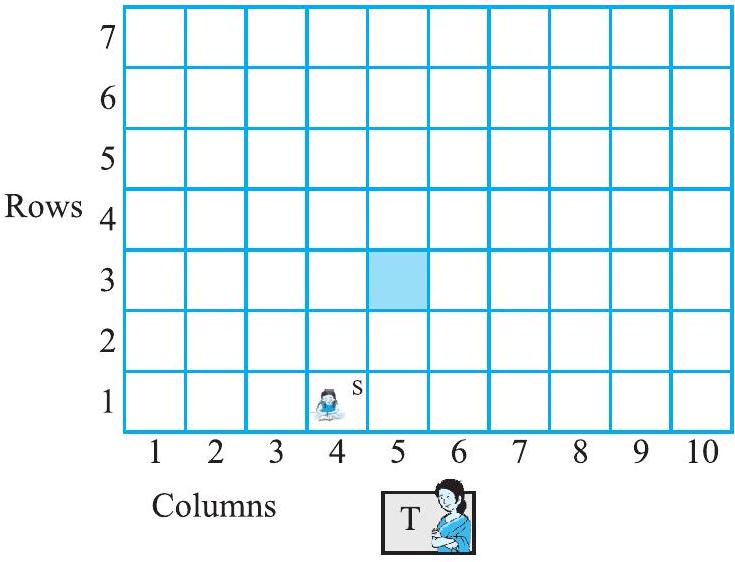
T शिक्षक की डेस्क को दर्शाता है S सोनिया की डेस्क को दर्शाता है

चित्र 3.3

ऊपर दी गई चर्चा में आपने देखा कि किसी भी तल में स्थित वस्तु की स्थिति को दो लंबवत रेखाओं की सहायता से दर्शाया जा सकता है। ‘बिंदु’ के मामले में हमें बिंदु की नीचे की रेखा से तथा कागज के बाएँ किनारे से दूरी चाहिए होती है। बैठने की योजना के मामले में हमें कॉलम की संख्या और पंक्ति की संख्या चाहिए होती है। यह सरल विचार बहुत दूरगामी परिणाम रखता है और गणित की एक अत्यंत महत्वपूर्ण शाखा ‘निर्देशांक ज्यामिति’ को जन्म देता है। इस अध्याय में हम निर्देशांक ज्यामिति की कुछ आधारभूत संकल्पनाओं से परिचय कराना चाहते हैं। आप इनके बारे में अपने उच्चतर कक्षाओं में और अधिक अध्ययन करेंगे। यह अध्ययन प्रारंभ में फ्रांसीसी दार्शनिक और गणितज्ञ रेने डेकार्ट द्वारा विकसित किया गया था।

रेन डेकार्ट, सत्रहवीं शताब्दी के महान फ्रांसीसी गणितज्ञ, बिस्तर पर लेटकर सोचना पसंद करते थे! एक दिन, जब वे बिस्तर पर विश्राम कर रहे थे, उन्होंने एक तल में किसी बिंदु की स्थिति वर्णित करने की समस्या हल की। उनकी विधि पुराने अक्षांश और देशांश के विचार का विकास थी। डेकार्ट के सम्मान में, तल में किसी बिंदु की स्थिति वर्णित करने के लिए प्रयुक्त प्रणाली को कार्टीजियन प्रणाली भी कहा जाता है।

रेन डेकार्ट (1596 -1650)

आकृति 3.4

3.2 कार्टीजियन प्रणाली

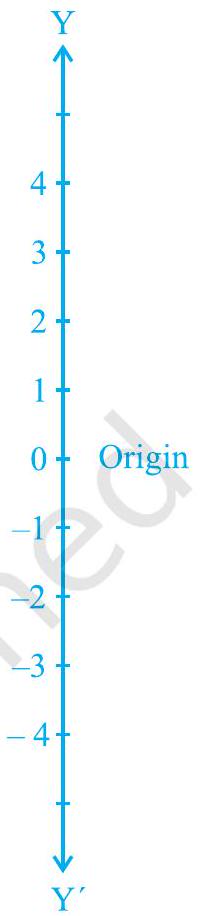
आपने ‘संख्या प्रणाली’ अध्याय में संख्या रेखा का अध्ययन किया है। संख्या रेखा पर, एक निश्चित बिंदु से दूरियों को समान इकाइयों में एक दिशा में धनात्मक और दूसरी दिशा में ऋणात्मक चिह्नित किया जाता है। वह बिंदु जिससे दूरियां चिह्नित की जाती हैं, मूल बिंदु कहलाता है। हम संख्याओं को प्रस्तुत करने के लिए संख्या रेखा का उपयोग करते हैं जिसमें एक रेखा पर समान दूरियों पर बिंदु चिह्नित किए जाते हैं। यदि एक इकाई दूरी संख्या ‘1’ को दर्शाती है, तो 3 इकाई दूरी संख्या ‘3’ को दर्शाती है, ‘0’ मूल बिंदु पर होता है। धनात्मक दिशा में मूल बिंदु से $r$ दूरी पर बिंदु संख्या $r$ को दर्शाता है। ऋणात्मक दिशा में मूल बिंदु से $r$ दूरी पर बिंदु संख्या $-r$ को दर्शाता है। संख्या रेखा पर विभिन्न संख्याओं के स्थान चित्र 3.5 में दिखाए गए हैं।

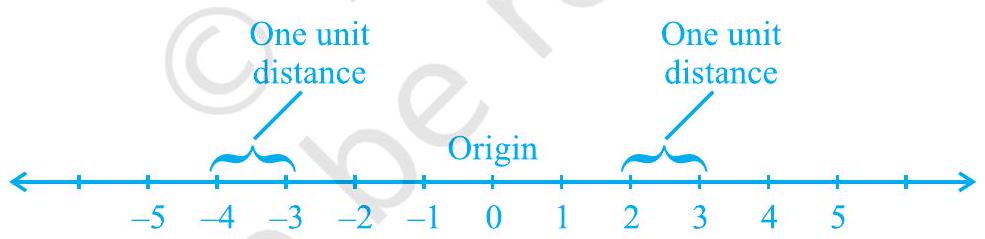
चित्र 3.5

डेकार्टेस ने दो ऐसी रेखाओं को समतल पर परस्पर लंबवत रखने का विचार आविष्कार किया, और समतल पर बिंदुओं को इन रेखाओं के संदर्भ में देखकर स्थित करने की विधि दी। लंबवत रेखाएं किसी भी दिशा में हो सकती हैं जैसे चित्र 3.6 में। लेकिन, जब हम चुनते हैं

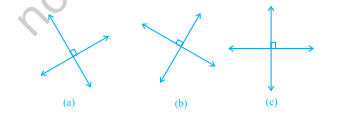
चित्र 3.6

इन दो रेखाओं द्वारा हम एक तल में बिंदु का स्थान निर्धारित करते हैं; इस अध्याय में एक रेखा क्षैतिज होगी और दूसरी ऊध्र्वाधर, जैसा कि आकृति 3.6(c) में है।
ये रेखाएँ वास्तव में इस प्रकार प्राप्त होती हैं: दो संख्या रेखाएँ लीजिए, उन्हें $\mathrm{X}^{\prime} \mathrm{X}$ और $\mathrm{Y}^{\prime} \mathrm{Y}$ कहिए। $\mathrm{X}^{\prime} \mathrm{X}$ को क्षैतिज रखिए [जैसा कि आकृति 3.7(a) में है] और उस पर संख्याएँ वैसे ही लिखिए जैसे संख्या रेखा पर लिखी होती हैं। हम $\mathrm{Y}^{\prime} \mathrm{Y}$ के साथ भी वही करते हैं, सिवाय इसके कि $\mathrm{Y}^{\prime} \mathrm{Y}$ क्षैतिज न होकर ऊध्र्वाधर है [आकृति 3.7(b)]।

(a)

(b) आकृति 3.7

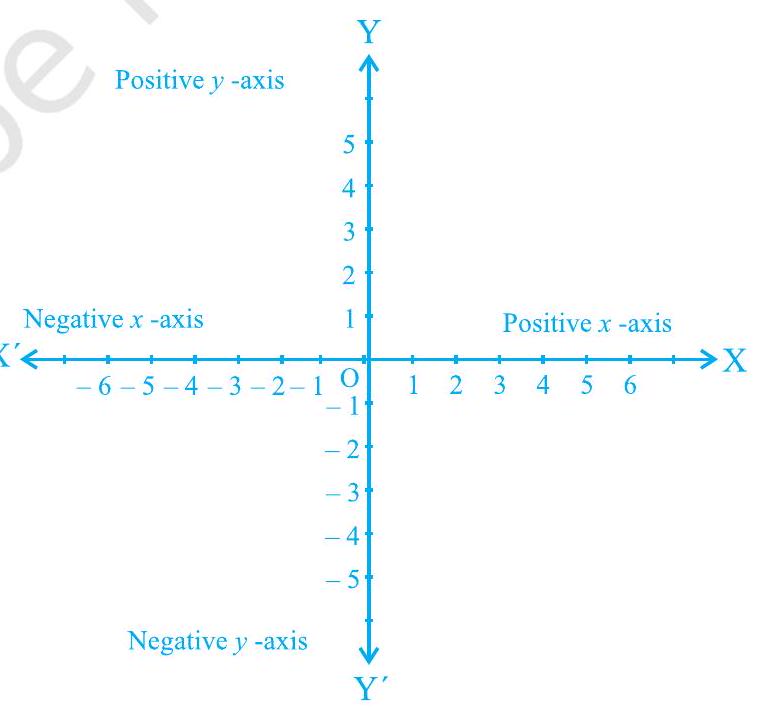
दोनों रेखाओं को इस प्रकार मिलाएं कि वे अपने शून्य बिंदुओं या मूल बिंदुओं पर एक-दूसरे को काटें (चित्र 3.8)। क्षैतिज रेखा $\mathrm{X}^{\prime} \mathrm{X}$ को $x$-अक्ष कहा जाता है और ऊर्ध्वाधर रेखा $Y^{\prime}$ को $y$-अक्ष कहा जाता है। जहाँ $X^{\prime} X$ और $Y^{\prime} Y$ एक-दूसरे को काटती हैं, उस बिंदु को मूल बिंदु कहा जाता है और इसे $\mathrm{O}$ द्वारा दर्शाया जाता है। चूँकि धनात्मक संख्याएँ $\mathrm{OX}$ और $\mathrm{OY}$ की दिशाओं में होती हैं, $\mathrm{OX}$ और $\mathrm{OY}$ को क्रमशः $x$-अक्ष और $y$-अक्ष की धनात्मक दिशाएँ कहा जाता है। इसी प्रकार, $\mathrm{OX}^{\prime}$ और $\mathrm{OY}^{\prime}$ को क्रमशः $x$-अक्ष और $y$-अक्ष की ऋणात्मक दिशाएँ कहा जाता हैं।

चित्र 3.8

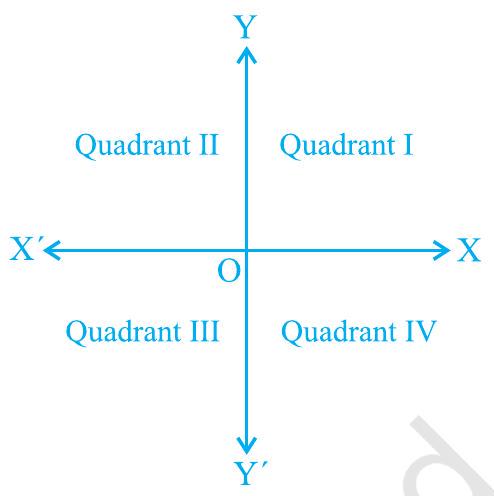
आप देखते हैं कि अक्ष (‘axis’ शब्द का बहुवचन) समतल को चार भागों में बाँटते हैं। इन चार भागों को चतुर्थांश (एक-चौथाई भाग) कहा जाता है, जिन्हें OX से प्रतिक्रम दिशा में I, II, III और IV क्रमांकित किया गया है (चित्र 3.9 देखें)। इसलिए, समतल में अक्ष और ये चतुर्थांश होते हैं। हम इस समतल को कार्टेशियन समतल, या निर्देशांक समतल, या xy-समतल कहते हैं। अक्षों को निर्देशांक अक्ष कहा जाता है।

चित्र 3.9

अब, आइए देखें कि यह प्रणाली गणित के लिए इतनी मूलभूत क्यों है और यह किस प्रकार उपयोगी है। निम्नलिखित आरेख पर विचार करें जहाँ अक्षों को ग्राफ पेपर पर खींचा गया है। आइए बिंदुओं $\mathrm{P}$ और $\mathrm{Q}$ की अक्षों से दूरियाँ देखें। इसके लिए, हम $x$-अक्ष पर लंब PM और $y$-अक्ष पर लंब PN खींचते हैं। इसी प्रकार, हम चित्र 3.10 में दिखाए गए अनुसार लंब QR और QS खींचते हैं।

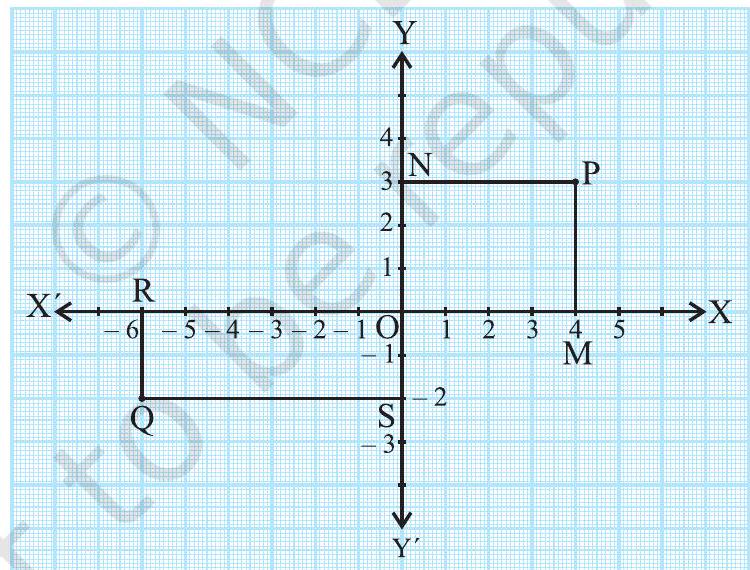
चित्र 3.10

आप पाते हैं कि

(i) बिंदु $\mathrm{P}$ की $y$-अक्ष से लंब दूरी, जो $x$-अक्ष की धनात्मक दिशा के अनुद्रत मापी गई है, $\mathrm{PN}=\mathrm{OM}=4$ इकाई है।

(ii) बिंदु $\mathrm{P}$ की $x$-अक्ष से लंब दूरी, जो $y$-अक्ष की धनात्मक दिशा के अनुद्रत मापी गई है, $\mathrm{PM}=\mathrm{ON}=3$ इकाई है।

(iii) बिंदु $\mathrm{Q}$ की $y$-अक्ष से लंब दूरी, जो $x$-अक्ष की ऋणात्मक दिशा के अनुद्रत मापी गई है, $\mathrm{OR}=\mathrm{SQ}=6$ इकाई है।

(iv) बिंदु $\mathrm{Q}$ की $x$-अक्ष से लंबवत दूरी, $y$-अक्ष की ऋणात्मक दिशा में मापी गई, $\mathrm{OS}=\mathrm{RQ}=2$ इकाई है।

अब, इन दूरियों का उपयोग करके, हम बिंदुओं का वर्णन कैसे करें ताकि कोई भ्रम न हो?

हम किसी बिंदु के निर्देशक निम्नलिखित नियमों का उपयोग करके लिखते हैं:

(i) किसी बिंदु का $x$-निर्देशक, $y$-अक्ष से उसकी लंबवत दूरी होती है, जिसे $x$-अक्ष के साथ मापा जाता है ($x$-अक्ष की धनात्मक दिशा में धनात्मक और $x$-अक्ष की ऋणात्मक दिशा में ऋणात्मक)। बिंदु $\mathrm{P}$ के लिए यह +4 है और $\mathrm{Q}$ के लिए -6 है। $x$-निर्देशक को भुज भी कहा जाता है।

(ii) किसी बिंदु का $y$-निर्देशक, $x$-अक्ष से उसकी लंबवत दूरी होती है, जिसे $y$-अक्ष के साथ मापा जाता है ($y$-अक्ष की धनात्मक दिशा में धनात्मक और $y$-अक्ष की ऋणात्मक दिशा में ऋणात्मक)। बिंदु $\mathrm{P}$ के लिए यह +3 है और $\mathrm{Q}$ के लिए -2 है। $y$-निर्देशक को कोटि भी कहा जाता है।

(iii) निर्देशक तल में किसी बिंदु के निर्देशक बताते समय, पहले $x$-निर्देशक आता है, फिर $y$-निर्देशक। हम निर्देशकों को कोष्ठक में रखते हैं।

अतः, $\mathrm{P}$ के निर्देशक $(4,3)$ हैं और $\mathrm{Q}$ के निर्देशक $(-6,-2)$ हैं।

ध्यान दें कि निर्देशक तल में किसी बिंदु का अद्वितीय वर्णन करते हैं। $(3,4)$ वही नहीं है जो $(4,3)$ है।

उदाहरण 1 : आकृति 3.11 देखें और निम्नलिखित कथनों को पूरा करें:

(i) बिंदु B की भुज और कोटि क्रमशः (\ldots \ldots) और (\ldots \ldots) हैं। इसलिए, B के निर्देशांक (__,__) हैं।

(ii) बिंदु M का x-निर्देशांक और y-निर्देशांक क्रमशः (\ldots) और (\ldots) हैं। इसलिए, M के निर्देशांक (__,__) हैं।

(iii) बिंदु L का x-निर्देशांक और y-निर्देशांक क्रमशः (\ldots) और (\ldots) हैं। इसलिए, L के निर्देशांक (__,__) हैं।

(iv) बिंदु S का x-निर्देशांक और y-निर्देशांक क्रमशः (\ldots \ldots) और (\ldots) हैं। इसलिए, S के निर्देशांक (__,__) हैं।

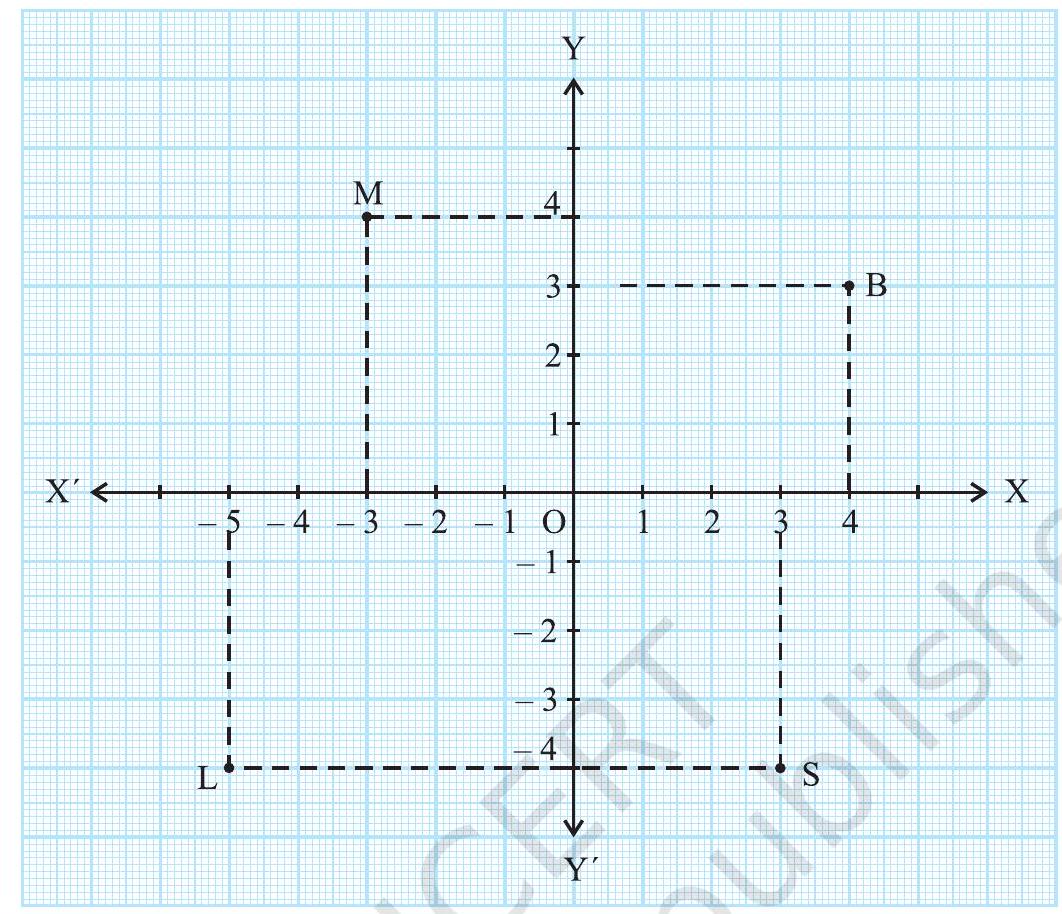
आकृति 3.11

हल: (i) चूँकि बिंदु B की y-अक्ष से दूरी 4 इकाई है, इसलिए बिंदु B का x-निर्देशांक या भुज 4 है। बिंदु B की x-अक्ष से दूरी 3 इकाई है; इसलिए बिंदु B का y-निर्देशांक, अर्थात् कोटि, 3 है। इसलिए बिंदु B के निर्देशांक $(4,3)$ हैं।

ऊपर (i) की तरह:

(ii) बिंदु M का x-निर्देशांक और y-निर्देशांक क्रमशः -3 और 4 हैं। इसलिए बिंदु M के निर्देशांक $(-3,4)$ हैं।

(iii) बिंदु L का x-निर्देशांक और y-निर्देशांक क्रमशः -5 और -4 हैं। इसलिए, बिंदु L के निर्देशांक $(-5,-4)$ हैं।

(iv) बिंदु S का x-निर्देशांक और y-निर्देशांक क्रमशः 3 और -4 हैं। इसलिए, बिंदु S के निर्देशांक $(3,-4)$ हैं।

उदाहरण 2 : आकृति 3.12 में अक्षों पर चिह्नित बिंदुओं के निर्देशांक लिखिए।

हल : आप देख सकते हैं कि :

(i) बिंदु A, y-अक्ष से +4 इकाई की दूरी पर है और x-अक्ष से शून्य दूरी पर है। इसलिए, A का x-निर्देशांक 4 है और y-निर्देशांक 0 है। इसलिए, A के निर्देशांक $(4,0)$ हैं।

(ii) B के निर्देशांक $(0,3)$ हैं। क्यों?

(iii) C के निर्देशांक $(-5,0)$ हैं। क्यों?

(iv) D के निर्देशांक $(0,-4)$ हैं। क्यों?

(v) E के निर्देशांक $\left(\frac{2}{3}, 0\right)$ हैं। क्यों?

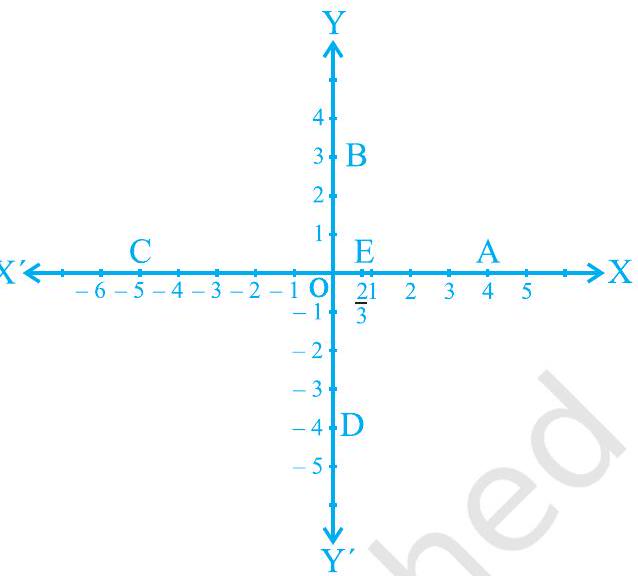
चूँकि $x$-अक्ष पर स्थित प्रत्येक बिंदु की $x$-अक्ष से दूरी शून्य होती है, इसलिए $x$-अक्ष पर स्थित प्रत्येक बिंदु का $y$-निर्देशांक सदा शून्य होता है। इस प्रकार, $x$-अक्ष पर किसी भी बिंदु के निर्देशांक $(x, 0)$ के रूप में होते हैं, जहाँ $x$ बिंदु की $y$-अक्ष से दूरी है। इसी प्रकार, $y$-अक्ष पर किसी भी बिंदु के निर्देशांक $(0, y)$ के रूप में होते हैं, जहाँ $y$ बिंदु की $x$-अक्ष से दूरी है। क्यों?

मूल बिंदु $\mathbf{O}$ के निर्देशांक क्या हैं? इसकी दोनों अक्षों से दूरी शून्य है, इसलिए इसकी भुज और कोटि दोनों शून्य हैं। अतः मूल बिंदु के निर्देशांक $(\mathbf{0}, \mathbf{0})$ हैं।

उपरोक्त उदाहरणों में आपने निम्नलिखित संबंध देखा होगा—किसी बिंदु के निर्देशांकों के चिह्नों और उस बिंदु के स्थित चतुर्थांश के बीच।

(i) यदि कोई बिंदु प्रथम चतुर्थांश में है, तो वह बिंदु $(+,+)$ के रूप में होगा, क्योंकि प्रथम चतुर्थांश धनात्मक $x$-अक्ष और धनात्मक $y$-अक्ष से घिरा है।

(ii) यदि कोई बिंदु द्वितीय चतुर्थांश में है, तो वह बिंदु $(-,+)$ के रूप में होगा, क्योंकि द्वितीय चतुर्थांश ऋणात्मक $x$-अक्ष और धनात्मक $y$-अक्ष से घिरा है।

(iii) यदि कोई बिंदु तृतीय चतुर्थांश में है, तो वह बिंदु $(-,-)$ के रूप में होगा, क्योंकि तृतीय चतुर्थांश ऋणात्मक $x$-अक्ष और ऋणात्मक $y$-अक्ष से घिरा है।

(iv) यदि कोई बिंदु चतुर्थ चतुर्थांश में है, तो वह बिंदु $(+,-)$ के रूप में होगा, क्योंकि चतुर्थ चतुर्थांध धनात्मक $x$-अक्ष और ऋणात्मक $y$-अक्ष से घिरा होता है (देखिए आकृति 3.13)।

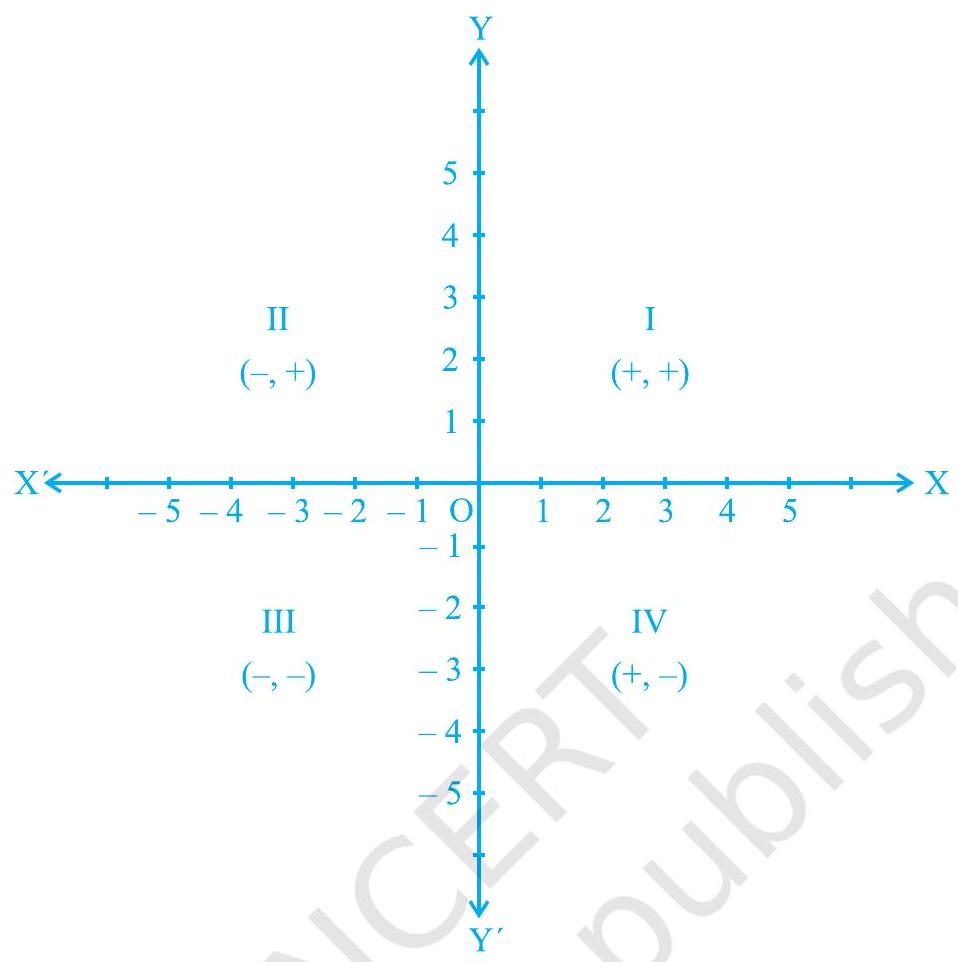
आकृति 3.13

टिप्पणी : उपरोक्त प्रणाली जिसे हमने समतल में बिंदु को वर्णित करने के लिए चर्चा की है, वह केवल एक परंपरा है, जिसे संपूर्ण विश्व में स्वीकार किया गया है। यह प्रणाली, उदाहरण के लिए, कोटि पहले और भुज दूसरे रूप में भी हो सकती थी। तथापि, किसी भी भ्रम से बचने के लिए संपूर्ण विश्व हमारे वर्णित प्रणाली का पालन करता है।

3.3 सारांश

इस अध्याय में आपने निम्नलिखित बिंदुओं का अध्ययन किया है :

1. किसी वस्तु या बिंदु की स्थिति को समतल में ज्ञात करने के लिए हमें दो लंबवत् रेखाओं की आवश्यकता होती है। उनमें से एक क्षैतिज होती है और दूसरी ऊर्ध्वाधर।

2. समतल को कार्तीय या निर्देशांक समतल कहा जाता है और रेखाओं को निर्देशांक अक्ष कहा जाता है।

3. क्षैतिज रेखा को $x$-अक्ष कहा जाता है और ऊर्ध्वाधर रेखा को $y$-अक्ष कहा जाता है।

4. निर्देशांक अक्ष समतल को चार भागों में विभाजित करते हैं जिन्हें चतुर्थांश कहा जाता है।

5. अक्षों के प्रतिच्छेदन बिंदु को मूल बिंदु कहा जाता है।

6. किसी बिंदु की $y$-अक्ष से दूरी को उसका $x$-निर्देशांक, या भुज, कहा जाता है, और बिंदु की $x$-अक्ष से दूरी को उसका $y$-निर्देशांक, या कोटि, कहा जाता है।

7. यदि किसी बिंदु की भुज $x$ है और कोटि $y$ है, तो $(x, y)$ को उस बिंदु के निर्देशांक कहा जाता है।

8. $x$-अक्ष पर स्थित किसी बिंदु के निर्देशांक $(x, 0)$ के रूप के होते हैं और $y$-अक्ष पर स्थित बिंदु के निर्देशांक $(0, y)$ के रूप के होते हैं।

9. मूल बिंदु के निर्देशांक $(0,0)$ होते हैं।

10. किसी बिंदु के निर्देशांक प्रथम चतुर्थांश में $(+,+)$, द्वितीय चतुर्थांश में $(-,+)$, तृतीय चतुर्थांश में $(-,-)$ और चतुर्थ चतुर्थांश में $(+,-)$ के रूप के होते हैं, जहाँ + एक धनात्मक वास्तविक संख्या को दर्शाता है और - एक ऋणात्मक वास्तविक संख्या को दर्शाता है।

11. यदि $x \neq y$, तो $(x, y) \neq(y, x)$, और $(x, y)=(y, x)$, यदि $x=y$।