2.1 परिचय

आपने पिछली कक्षाओं में बीजीय व्यंजकों, उनके योग, व्यवकलन, गुणा और भाग का अध्ययन किया है। आपने यह भी अध्ययन किया है कि कुछ बीजीय व्यंजकों को गुणनफल के रूप में कैसे व्यक्त किया जाता है। आपको ये बीजीय सर्वसमिकाएँ याद होंगी :

और

$$ \begin{aligned} & (x+y)^{2}=x^{2}+2 x y+y^{2} \\ & (x-y)^{2}=x^{2}-2 x y+y^{2} \\ & x^{2}-y^{2}=(x+y)(x-y) \end{aligned} $$

और उनके उपयोग को गुणनफल के रूप में व्यक्त करने में। इस अध्याय में, हम एक विशेष प्रकार के बीजीय व्यंजक, जिसे बहुपद कहा जाता है, और उससे संबंधित पारिभाषिक शब्दों के साथ अपने अध्ययन की शुरुआत करेंगे। हम शेषफल प्रमेय और गुणनफल प्रमेय का भी अध्ययन करेंगे और उनके उपयोग को बहुपदों के गुणनफल के रूप में व्यक्त करने में करेंगे। उपरोक्त के अतिरिक्त, हम कुछ और बीजीय सर्वसमिकाओं और उनके उपयोग को गुणनफल के रूप में व्यक्त करने और कुछ दिए गए व्यंजकों के मान निकालने में करेंगे।

2.2 एक चर में बहुपद

आइए प्रारंभ करें याद करके कि एक चर को एक प्रतीक द्वारा दर्शाया जाता है जो कोई भी वास्तविक मान ले सकता है। हम चरों को दर्शाने के लिए अक्षरों $x, y, z$, आदि का उपयोग करते हैं। ध्यान दें कि $2 x, 3 x,-x,-\frac{1}{2} x$ बीजीय व्यंजक हैं। ये सभी व्यंजक (एक नियतांक) $\times x$ के रूप के हैं। अब मान लीजिए हम एक ऐसा व्यंजक लिखना चाहते हैं जो (एक नियतांक) $\times($ एक चर $)$ है और हम नहीं जानते कि नियतांक क्या है। ऐसी स्थितियों में, हम नियतांक को $a, b, c$, आदि लिखते हैं। तो व्यंजक होगा $a x$, मान लीजिए।

हालांकि, एक स्थिरांक को दर्शाने वाले अक्षर और एक चर को दर्शाने वाले अक्षर के बीच अंतर होता है। स्थिरांकों के मान किसी विशेष परिस्थिति में समान रहते हैं, अर्थात् दी गई समस्या में स्थिरांकों के मान नहीं बदलते, लेकिन चर का मान बदलता रहता है।

अब, 3 इकाई भुजा वाले एक वर्ग पर विचार करें (देखें Fig. 2.1)। इसका परिमाप क्या है? आप जानते हैं कि वर्ग का परिमाप इसकी चारों भुजाओं की लंबाइयों का योग होता है। यहाँ प्रत्येक भुजा 3 इकाई है। इसलिए, इसका परिमाप $4 \times 3$, अर्थात् 12 इकाई है। यदि वर्ग की प्रत्येक भुजा 10 इकाई हो तो परिमाप क्या होगा? परिमाप $4 \times 10$, अर्थात् 40 इकाई है। यदि प्रत्येक भुजा की लंबाई $x$ इकाई हो (देखें Fig. 2.2), तो परिमाप $4 x$ इकाई द्वारा दिया जाता है। इसलिए, जैसे-जैसे भुजा की लंबाई बदलती है, परिमाप भी बदलता है।

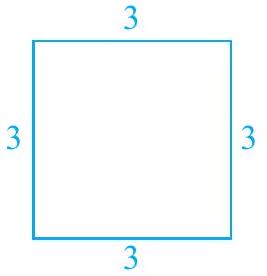
Fig. 2.1

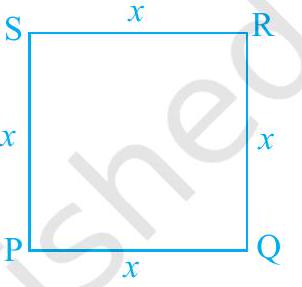
Fig. 2.2 $x$ में बहुपद है। इसी प्रकार, $3 y^{2}+5 y$ चर $y$ में एक बहुपद है और $t^{2}+4$ चर $t$ में एक बहुपद है।

बहुपद $x^{2}+2 x$ में व्यंजक $x^{2}$ और $2 x$ को बहुपद के पद कहा जाता है। इसी प्रकार, बहुपद $3 y^{2}+5 y+7$ के तीन पद हैं, अर्थात्, $3 y^{2}, 5 y$ और 7। क्या आप बहुपद $-x^{3}+4 x^{2}+7 x-2$ के पद लिख सकते हैं? इस बहुपद के 4 पद हैं, अर्थात्, $-x^{3}, 4 x^{2}, 7 x$ और -2।

बहुपद के प्रत्येक पद का एक गुणांक होता है। इसलिए, $-x^{3}+4 x^{2}+7 x-2$ में, $x^{3}$ का गुणांक -1 है, $x^{2}$ का गुणांक 4 है, $x$ का गुणांक 7 है और -2, $x^{0}$ का गुणांक है (याद रखें, $x^{0}=1$)। क्या आप जानते हैं कि $x^{2}-x+7$ में $x$ का गुणांक क्या है? यह -1 है।

2 भी एक बहुपद है। वास्तव में, $2,-5,7$, आदि स्थिर बहुपदों के उदाहरण हैं। स्थिर बहुपद 0 को शून्य बहुपद कहा जाता है। यह सभी बहुपदों के संग्रह में एक बहुत महत्वपूर्ण भूमिका निभाता है, जैसा कि आप उच्च कक्षाओं में देखेंगे।

अब, बीजगणितीय व्यंजकों पर विचार करें जैसे $x+\frac{1}{x}, \sqrt{x}+3$ और $\sqrt[3]{y}+y^{2}$। क्या आप जानते हैं कि आप $x+\frac{1}{x}=x+x^{-1}$ लिख सकते हैं? यहाँ, दूसरे पद का घातांक, अर्थात्, $x^{-1}$ का मान -1 है, जो एक पूर्ण संख्या नहीं है। इसलिए, यह बीजगणितीय व्यंजक एक बहुपद नहीं है।

फिर, $\sqrt{x}+3$ को $x^{\frac{1}{2}}+3$ के रूप में लिखा जा सकता है। यहाँ $x$ का घातांक $\frac{1}{2}$ है, जो एक पूर्ण संख्या नहीं है। तो, क्या $\sqrt{x}+3$ एक बहुपद है? नहीं, यह नहीं है। $\sqrt[3]{y}+y^{2}$ के बारे में क्या? यह भी एक बहुपद नहीं है (क्यों?)।

यदि किसी बहुपद में चर $x$ है, तो हम उस बहुपद को $p(x)$, या $q(x)$, या $r(x)$ आदि द्वारा दर्शा सकते हैं। तो, उदाहरण के लिए, हम लिख सकते हैं:

$$ \begin{aligned} & p(x)=2 x^{2}+5 x-3 \\ & q(x)=x^{3}-1 \\ & r(y)=y^{3}+y+1 \\ & s(u)=2-u-u^{2}+6 u^{5} \end{aligned} $$

एक बहुपद में कोई भी (परिमित) संख्या में पद हो सकते हैं। उदाहरण के लिए, $x^{150}+x^{149}+\ldots$ $+x^{2}+x+1$ एक बहुपद है जिसमें 151 पद हैं।

बहुपदों $2 x, 2,5 x^{3},-5 x^{2}, y$ और $u^{4}$ पर विचार करें। क्या आप देखते हैं कि इनमें से प्रत्येक बहुपद में केवल एक ही पद है? केवल एक पद वाले बहुपदों को एकपदी (monomials) कहा जाता है (‘mono’ का अर्थ है ‘एक’)।

अब निम्नलिखित प्रत्येक बहुपदों को देखें:

$p(x)=x+1, \quad q(x)=x^{2}-x,$ $r(y)=y^{30}+1, \quad t(u)=u^{43}-u^{2}$

इनमें से प्रत्येक में कितने पद हैं? इनमें से प्रत्येक बहुपद में केवल दो पद हैं। केवल दो पद वाले बहुपदों को द्विपदी (binomials) कहा जाता है (‘bi’ का अर्थ है ‘दो’)।

इसी प्रकार, केवल तीन पद वाले बहुपदों को त्रिपदी (trinomials) कहा जाता है (’tri’ का अर्थ है ‘तीन’)। त्रिपदी के कुछ उदाहरण हैं

$$ \begin{array}{ll} p(x)=x+x^{2}+\pi, & q(x)=\sqrt{2}+x-x^{2}, \\ r(u)=u+u^{2}-2, & t(y)=y^{4}+y+5 \end{array} $$

अब, बहुपद $p(x)=3 x^{7}-4 x^{6}+x+9$ को देखिए। इसमें $x$ की सबसे बड़ी घात वाला पद कौन-सा है? यह $3 x^{7}$ है। इस पद में $x$ का घातांक 7 है। इसी प्रकार, बहुपद $q(y)=5 y^{6}-4 y^{2}-6$ में $y$ की सबसे बड़ी घात वाला पद $5 y^{6}$ है और इस पद में $y$ का घातांक 6 है। हम किसी बहुपद में चर की सबसे बड़ी घात को बहुपद की घात कहते हैं। अतः बहुपद $3 x^{7}-4 x^{6}+x+9$ की घात 7 है और बहुपद $5 y^{6}-4 y^{2}-6$ की घात 6 है। किसी अशून्य नियत बहुपद की घात शून्य होती है।

उदाहरण 1 : नीचे दिए गए प्रत्येक बहुपद की घात ज्ञात कीजिए:

(i) $x^{5}-x^{4}+3$

(ii) $2-y^{2}-y^{3}+2 y^{8}$

(iii) 2

हल : (i) चर की सबसे बड़ी घात 5 है। अतः बहुपद की घात 5 है।

(ii) चर की सबसे बड़ी घात 8 है। अतः बहुपद की घात 8 है।

(iii) यहाँ केवल एक पद 2 है जिसे $2 x^{0}$ के रूप में लिखा जा सकता है। अतः $x$ का घातांक 0 है। इसलिए बहुपद की घात 0 है।

अब बहुपदों $p(x)=4 x+5, q(y)=2 y, r(t)=t+\sqrt{2}$ और $s(u)=3-u$ को देखिए। क्या आप इन सभी में कुछ समान देखते हैं? इनमें से प्रत्येक बहुपद की घात एक है। घात एक वाले बहुपद को रैखिक बहुपद कहा जाता है। एक चर वाले कुछ और रैखिक बहुपद हैं $2 x-1, \sqrt{2} y+1,2-u$। अब, कोशिश करें और $x$ में तीन पदों वाला एक रैखिक बहुपद खोजें? आप इसे नहीं खोज पाएंगे क्योंकि $x$ में रैखिक बहुपद में अधिकतम दो पद हो सकते हैं। इसलिए, $x$ में कोई भी रैखिक बहुपद $a x+b$ के रूप में होगा, जहाँ $a$ और $b$ स्थिरांक हैं और $a \neq 0$ (क्यों?)। इसी प्रकार, $a y+b$, $y$ में एक रैखिक बहुपद है।

अब बहुपदों पर विचार करें :

$$2 x^{2}+5,5 x^{2}+3 x+\pi, x^{2} \text { और } x^{2}+\frac{2}{5} x$$

क्या आप सहमत हैं कि ये सभी घात दो के हैं? घात दो वाले बहुपद को द्विघात बहुपद कहा जाता है। द्विघात बहुपद के कुछ उदाहरण हैं $5-y^{2}$, $4 y+5 y^{2}$ और $6-y-y^{2}$। क्या आप एक चर वाला चार भिन्न पदों वाला द्विघात बहुपद लिख सकते हैं? आप पाएंगे कि एक चर वाले द्विघात बहुपद में अधिकतम 3 पद होंगे। यदि आप कुछ और द्विघात बहुपदों की सूची बनाते हैं, तो आप पाएंगे कि $x$ में कोई भी द्विघात बहुपद $a x^{2}+b x+c$ के रूप में होता है, जहाँ $a \neq 0$ और $a, b, c$ स्थिरांक हैं। इसी प्रकार, $y$ में द्विघात बहुपद $a y^{2}+b y+c$ के रूप में होगा, बशर्ते $a \neq 0$ और $a, b, c$ स्थिरांक हों।

हम एक घात तीन का बहुपद एक घन बहुपद कहते हैं। $x$ में घन बहुपद के कुछ उदाहरण हैं: $4 x^{3}, 2 x^{3}+1,5 x^{3}+x^{2}, 6 x^{3}-x, 6-x^{3}, 2 x^{3}+4 x^{2}+6 x+7$। आपको क्या लगता है, एक चर वाला घन बहुपद अधिकतम कितने पदों का हो सकता है? यह अधिकतम 4 पदों का हो सकता है। इन्हें इस रूप में लिखा जा सकता है: $a x^{3}+b x^{2}+c x+d$, जहाँ $a \neq 0$ और $a, b, c$ तथा $d$ अचर हैं।

अब जब आपने देख लिया है कि घात 1, घात 2 या घात 3 का बहुपद कैसा दिखता है, तो क्या आप किसी प्राकृतिक संख्या $n$ के लिए एक चर वाला घात $n$ का बहुपद लिख सकते हैं? एक चर $x$ वाला घात $n$ का बहुपद इस रूप का एक व्यंजक होता है:

$$a_{n} x^{n}+a_{n-1} x^{n-1}+\ldots+a_{1} x+a_{0}$$

जहाँ $a_{0}, a_{1}, a_{2}, \ldots, a_{n}$ अचर हैं और $a_{n} \neq 0$।

विशेष रूप से, यदि $a_{0}=a_{1}=a_{2}=a_{3}=\ldots=a_{n}=0$ (सभी अचर शून्य हैं), तो हमें शून्य बहुपद प्राप्त होता है, जिसे 0 द्वारा दर्शाया जाता है। शून्य बहुपद की घात क्या है? शून्य बहुपद की घात परिभाषित नहीं होती है।

अब तक हमने केवल एक चर वाले बहुपदों पर विचार किया है। हमारे पास एक से अधिक चर वाले बहुपद भी हो सकते हैं। उदाहरण के लिए, $x^{2}+y^{2}+x y z$ (जहाँ चर $x, y$ और $z$ हैं) तीन चरों का एक बहुपद है। इसी तरह, $p^{2}+q^{10}+r$ (जहाँ चर $p, q$ और $r$ हैं), $u^{3}+v^{2}$ (जहाँ चर $u$ और $v$ हैं) क्रमशः तीन और दो चरों के बहुपद हैं। आप ऐसे बहुपदों का विस्तार से अध्ययन बाद में करेंगे।

2.3 बहुपद के शून्य

बहुपद $p(x)=5 x^{3}-2 x^{2}+3 x-2$ पर विचार कीजिए।

यदि हम $p(x)$ में हर जगह $x$ के स्थान पर 1 रखें, तो हमें प्राप्त होता है

$$ \begin{aligned} p(1) & =5 \times(1)^{3}-2 \times(1)^{2}+3 \times(1)-2 \ & =5-2+3-2 \ & =4 \end{aligned} $$

इसलिए, हम कहते हैं कि $x=1$ पर $p(x)$ का मान 4 है।

इसी प्रकार,

$p(0) =5(0)^{3}-2(0)^{2}+3(0)-2$

$$ =-2 $$

क्या आप $p(-1)$ ज्ञात कर सकते हैं?

उदाहरण 2 : निम्नलिखित प्रत्येक बहुपद का चिह्नित चर मानों पर मान ज्ञात कीजिए:

(i) $p(x)=5 x^{2}-3 x+7$ at $x=1$.

(ii) $q(y)=3 y^{3}-4 y+\sqrt{11}$ at $y=2$.

(iii) $p(t)=4 t^{4}+5 t^{3}-t^{2}+6$ at $t=a$.

हल : (i) $p(x)=5 x^{2}-3 x+7$

बहुपद $p(x)$ का मान $x=1$ पर निम्न प्रकार से दिया गया है

$$ \begin{aligned} p(1) & =5(1)^{2}-3(1)+7 \ & =5-3+7=9 \end{aligned} $$

(ii) $q(y)=3 y^{3}-4 y+\sqrt{11}$

बहुपद $q(y)$ का मान $y=2$ पर निम्न प्रकार से दिया गया है

$$q(2)=3(2)^{3}-4(2)+\sqrt{11}=24-8+\sqrt{11}=16+\sqrt{11}$$

(iii) $p(t)=4 t^{4}+5 t^{3}-t^{2}+6$

बहुपद $p(t)$ का मान $t=a$ पर निम्न प्रकार से दिया गया है

$$ p(a)=4 a^{4}+5 a^{3}-a^{2}+6 $$

अब, बहुपद $p(x)=x-1$ पर विचार कीजिए।

$p(1)$ क्या है? ध्यान दीजिए : $p(1)=1-1=0$।

चूँकि $p(1)=0$, इसलिए हम कहते हैं कि 1 बहुपद $p(x)$ का एक शून्य है।

इसी प्रकार, आप यह जाँच सकते हैं कि 2, $q(x)$ का शून्य है, जहाँ $q(x)=x-2$।

सामान्यतः, हम कहते हैं कि बहुपद $p(x)$ का एक शून्य एक ऐसी संख्या $c$ है जिससे $p(c)=0$ हो।

आपने देखा होगा कि बहुपद $x-1$ का शून्य इसे 0 के बराबर करके प्राप्त किया जाता है, अर्थात् $x-1=0$, जो $x=1$ देता है। हम कहते हैं कि $p(x)=0$ एक बहुपद समीकरण है और 1 बहुपद समीकरण $p(x)=0$ का मूल है। इसलिए हम कहते हैं कि 1 बहुपद $x-1$ का शून्य है, या बहुपद समीकरण $x-1=0$ का मूल है।

अब, स्थिर बहुपद 5 पर विचार कीजिए। क्या आप बता सकते हैं कि इसका शून्य क्या है? इसका कोई शून्य नहीं है क्योंकि $5 x^{0}$ में $x$ को किसी भी संख्या से प्रतिस्थापित करने पर भी हमें 5 ही प्राप्त होता है। वास्तव में, एक अशून्य स्थिर बहुपद का कोई शून्य नहीं होता। शून्य बहुपद के शून्यों के बारे में क्या? परंपरा से, प्रत्येक वास्तविक संख्या शून्य बहुपद का शून्य है।

उदाहरण 3 : जाँच कीजिए कि -2 और 2 बहुपद $x+2$ के शून्य हैं या नहीं।

हल : मान लीजिए $p(x)=x+2$।

तब $p(2)=2+2=4, p(-2)=-2+2=0$

इसलिए, -2 बहुपद $x+2$ का शून्य है, लेकिन 2 नहीं है।

उदाहरण 4 : बहुपद $p(x)=2 x+1$ का एक शून्य ज्ञात कीजिए।

हल : $p(x)$ का एक शून्य खोजना, समीकरण को हल करने के समान है

$$ p(x)=0 $$

अब,

$$ 2 x+1=0 \text { हमें } x=-\frac{1}{2} \text { देता है } $$

इसलिए, $-\frac{1}{2}$ बहुपद $2 x+1$ का शून्य है।

अब, यदि $p(x)=a x+b, a \neq 0$, एक रैखिक बहुपद है, तो हम $p(x)$ का शून्य कैसे खोज सकते हैं? उदाहरण 4 ने आपको कुछ विचार दिया होगा। बहुपद $p(x)$ का शून्य खोजना, बहुपद समीकरण $p(x)=0$ को हल करने के समान है।

अब, $p(x)=0$ का अर्थ है

$$ \begin{aligned} a x+b & =0, a \neq 0 \ a x & =-b \ x & =-\frac{b}{a} . \end{aligned} $$

इसलिए,

इसलिए, $x=-\frac{b}{a}$ बहुपद $p(x)$ का एकमात्र शून्यक है, अर्थात् एक रैखिक बहुपद का एक और केवल एक ही शून्यक होता है।

अब हम कह सकते हैं कि 1, $x-1$ का शून्यक है, और -2, $x+2$ का शून्यक है।

उदाहरण 5 : सत्यापित कीजिए कि क्या 2 और 0 बहुपद $x^{2}-2 x$ के शून्यक हैं।

हल : मान लीजिए

$p(x)=x^{2}-2 x$

तब $p(2)=2^{2}-4=4-4=0$

और $p(0)=0-0=0$

अतः, 2 और 0 दोनों ही बहुपद $x^{2}-2 x$ के शून्यक हैं।

आइए अब हम अपने प्रेक्षणों की सूची बनाते हैं:

(i) किसी बहुपद का शून्यक 0 होना आवश्यक नहीं है।

(ii) 0 किसी बहुपद का शून्यक हो सकता है।

(iii) प्रत्येक रैखिक बहुपद का एक और केवल एक ही शून्यक होता है।

(iv) किसी बहुपद के एक से अधिक शून्यक हो सकते हैं।

2.4 बहुपदों का गुणनखंडन

आइए अब हम उपरोक्त उदाहरण 10 की स्थिति को और गहराई से देखें। यह हमें बताता है कि चूँकि शेषफल, $q\left(-\frac{1}{2}\right)=0$ है, $(2 t+1)$, $q(t)$ का एक गुणनखंड है, अर्थात् $q(t)=(2 t+1) g(t)$ किसी बहुपद $g(t)$ के लिए। यह निम्नलिखित प्रमेय का एक विशेष case है।

गुणनखंड प्रमेय : यदि $p(x)$ एक बहुपद है जिसकी कोटि $n \geq 1$ है और $a$ कोई वास्तविक संख्या है, तो (i) $x-a$, $p(x)$ का गुणनखंड है, यदि $p(a)=0$, और (ii) $p(a)=0$, यदि $x-a$, $p(x)$ का गुणनखंड है।

प्रमाण : शेषफल प्रमेय द्वारा, $p(x)=(x-a) q(x)+p(a)$।

(i) यदि $p(a)=0$, तो $p(x)=(x-a) q(x)$, जो दर्शाता है कि $x-a$, $p(x)$ का गुणनखंड है।

(ii) चूँकि $x-a$, $p(x)$ का गुणनखंड है, $p(x)=(x-a) g(x)$ किसी बहुपद $g(x)$ के लिए। इस स्थिति में, $p(a)=(a-a) g(a)=0$।

उदाहरण 6 : जाँच कीजिए कि क्या $x+2$ एक गुणनखंड है $x^{3}+3 x^{2}+5 x+6$ और $2 x+4$ का।

हल : $x+2$ का शून्य -2 है। मान लीजिए $p(x)=x^{3}+3 x^{2}+5 x+6$ और $s(x)=2 x+4$ तब,

$$ \begin{aligned} p(-2) & =(-2)^{3}+3(-2)^{2}+5(-2)+6 \ & =-8+12-10+6 \ & =0 \end{aligned} $$

इसलिए, गुणनखंड प्रमेय से, $x+2$ एक गुणनखंड है $x^{3}+3 x^{2}+5 x+6$ का।

पुनः,

$$ s(-2)=2(-2)+4=0 $$

इसलिए, $x+2$ एक गुणनखंड है $2 x+4$ का। वास्तव में, आप इसे गुणनखंड प्रमेय लगाए बिना भी जाँच सकते हैं, क्योंकि $2 x+4=2(x+2)$।

उदाहरण 7 : $k$ का मान ज्ञात कीजिए, यदि $x-1$ एक गुणनखंड है $4 x^{3}+3 x^{2}-4 x+k$ का।

हल : चूँकि $x-1$ एक गुणनखंड है $p(x)=4 x^{3}+3 x^{2}-4 x+k$ का, $p(1)=0$

अब,

$$ \begin{aligned} & p(1)=0 \text{ होगा। } \ & p(1)=4(1)^{3}+3(1)^{2}-4(1)+k \end{aligned} $$

इसलिए,

$$ \begin{aligned} 4+3-4+k & =0 \ k & =-3 \end{aligned} $$

अब हम गुणनखंड प्रमेय का उपयोग करके कुछ बहुपदों को 2 और 3 घात तक गुणनखंडित करेंगे। आप पहले से ही द्विघात बहुपद जैसे $x^{2}+l x+m$ के गुणनखंडन से परिचित हैं। आपने इसे मध्य पद $l x$ को $a x+b x$ में इस प्रकार विभाजित करके गुणनखंडित किया था कि $a b=m$ हो। तब $x^{2}+l x+m=(x+a)(x+b)$। अब हम द्विघात बहुपदों को $a x^{2}+b x+c$ प्रकार के गुणनखंडित करने का प्रयास करेंगे, जहाँ $a \neq 0$ और $a, b, c$ नियतांक हैं।

बहुपद $a x^{2}+b x+c$ का मध्य पद को विभाजित करके गुणनखंडन इस प्रकार है:

मान लीजिए इसके गुणनखंड $(p x+q)$ और $(r x+s)$ हैं। तब $\frac{3 x^{2}}{x}=3 x=$ भागफल का प्रथम पद

$a x^{2}+b x+c=(p x+q)(r x+s)=p r x^{2}+(p s+q r) x+q s$

$x^{2}$ के गुणांकों की तुलना करने पर, हमें मिलता है $a=p r$।

इसी प्रकार, $x$ के गुणांकों की तुलना करने पर, हमें मिलता है $b=p s+q r$।

और, अचर पदों की तुलना करने पर, हमें मिलता है $c=q s$।

यह हमें दिखाता है कि $b$ दो संख्याओं $p s$ और $q r$ का योग है, जिनका गुणनफल $(p s)(q r)=(p r)(q s)=a c$ है।

इसलिए, $a x^{2}+b x+c$ का गुणनखंड करने के लिए, हमें $b$ को दो ऐसी संख्याओं के योग के रूप में लिखना होगा जिनका गुणनफल $a c$ हो। यह उदाहरण 13 से स्पष्ट होगा।

उदाहरण 8 : मध्य पद को विभाजित करके और गुणनखंड प्रमेय का उपयोग करके $6 x^{2}+17 x+5$ का गुणनखंडन कीजिए।

हल 1 : (विभाजन विधि द्वारा) : यदि हम दो संख्याएँ $p$ और $q$ ऐसी खोज सकें कि $p+q=17$ और $p q=6 \times 5=30$, तो हम गुणनखंड प्राप्त कर सकते हैं।

तो, आइए 30 के गुणनखंडों के युग्मों को देखें। कुछ हैं 1 और 30, 2 और 15, 3 और 10, 5 और 6। इन युग्मों में से, 2 और 15 हमें $p+q=17$ देते हैं।

इसलिए,

$$ \begin{aligned} 6 x^{2}+17 x+5 & =6 x^{2}+(2+15) x+5 \\ & =6 x^{2}+2 x+15 x+5 \\ & =2 x(3 x+1)+5(3 x+1) \\ & =(3 x+1)(2 x+5) \end{aligned} $$

हल 2 : (गुणनखंड प्रमेय का उपयोग करके)

$6 x^{2}+17 x+5=6\left(x^{2}+\frac{17}{6} x+\frac{5}{6}\right)=6 p(x)$, मान लीजिए। यदि $a$ और $b$, $p(x)$ के मूल हैं, तो $6 x^{2}+17 x+5=6(x-a)(x-b)$। इसलिए, $a b=\frac{5}{6}$।

आइए $a$ और $b$ के लिए कुछ संभावनाओं को देखें।

वे $\pm \frac{1}{2}, \pm \frac{1}{3}, \pm \frac{5}{3}, \pm \frac{5}{2}, \pm 1$ हो सकते हैं।

अब, $p\left(\frac{1}{2}\right)=\frac{1}{4}+\frac{17}{6}\left(\frac{1}{2}\right)+\frac{5}{6} \neq 0$।

लेकिन $p\left(\frac{-1}{3}\right)=0$।

इसलिए, $\left(x+\frac{1}{3}\right)$, $p(x)$ का एक गुणनखंड है।

इसी प्रकार, प्रयास से आप पा सकते हैं कि $\left(x+\frac{5}{2}\right)$ भी $p(x)$ का एक गुणनखंड है।

इसलिए,

$$ \begin{aligned} 6 x^{2}+17 x+5 & =6\left(x+\frac{1}{3}\right)\left(x+\frac{5}{2}\right) \ & =6\left(\frac{3 x+1}{3}\right)\left(\frac{2 x+5}{2}\right) \ & =(3 x+1)(2 x+5) \end{aligned} $$

उपरोक्त उदाहरण में विभाजन विधि का प्रयोग अधिक कुशल प्रतीत होता है। हालांकि, आइए एक अन्य उदाहरण पर विचार करें।

उदाहरण 9 : गुणनखंड प्रमेय का प्रयोग करके $y^{2}-5 y+6$ का गुणनखंडन कीजिए।

हल : मान लीजिए $p(y)=y^{2}-5 y+6$। अब, यदि $p(y)=(y-a)(y-b)$ है, तो आप जानते हैं कि स्थिर पद $a b$ होगा। इसलिए, $a b=6$। इसलिए $p(y)$ के गुणनखंडों की खोज करने के लिए हम 6 के गुणनखंडों को देखते हैं।

6 के गुणनखंड 1, 2 और 3 हैं।

अब, $p(2)=2^{2}-(5 \times 2)+6=0$

इसलिए, $y-2$, $p(y)$ का एक गुणनखंड है।

साथ ही, $p(3)=3^{2}-(5 \times 3)+6=0$

इसलिए, $y-3$ भी $y^{2}-5 y+6$ का एक गुणनखंड है।

इसलिए, $y^{2}-5 y+6=(y-2)(y-3)$

ध्यान दीजिए कि $y^{2}-5 y+6$ का गुणनखंडन मध्य पद $-5 y$ को विभाजित करके भी किया जा सकता है।

अब, आइए घन बहुपदों के गुणनखंडन पर विचार करें। यहाँ विभाजन विधि प्रारंभ में उपयुक्त नहीं होगी। हमें पहले कम से कम एक गुणनखंड खोजने की आवश्यकता है, जैसा कि आप निम्नलिखित उदाहरण में देखेंगे।

उदाहरण 10 : $x^{3}-23 x^{2}+142 x-120$ का गुणनखंडन कीजिए।

हल: माना $p(x)=x^{3}-23 x^{2}+142 x-120$

हम अब -120 के सभी गुणनखोजों को देखेंगे। इनमें से कुछ हैं

$\pm 1, \pm 2, \pm 3, \pm 4, \pm 5, \pm 6, \pm 8, \pm 10, \pm 12, \pm 15, \pm 20, \pm 24, \pm 30, \pm 60$.

प्रयास से हम पाते हैं कि $p(1)=0$। इसलिए $x-1$, $p(x)$ का एक गुणनखंड है।

अब हम देखते हैं कि $x^{3}-23 x^{2}+142 x-120=x^{3}-x^{2}-22 x^{2}+22 x+120 x-120$

$$ \begin{aligned} & =x^{2}(x-1)-22 x(x-1)+120(x-1) \quad(\text { क्यों? }) \\ & =(x-1)\left(x^{2}-22 x+120\right) \quad[(x-1) \text{ उभयनिष्ट लेकर}] \end{aligned} $$

हम यह $p(x)$ को $x-1$ से भाग देकर भी प्राप्त कर सकते थे।

अब $x^{2}-22 x+120$ को या तो मध्य पद को विभाजित करके या गुणनखंड प्रमेय का प्रयोग करके गुणनखंडित किया जा सकता है। मध्य पद को विभाजित करके हम पाते हैं:

$$ \begin{aligned} x^{2}-22 x+120 & =x^{2}-12 x-10 x+120 \\ & =x(x-12)-10(x-12) \\ & =(x-12)(x-10) \end{aligned} $$

इसलिए, $\quad x^{3}-23 x^{2}-142 x-120=(x-1)(x-10)(x-12)$

2.5 बीजीय सर्वसमिकाएँ

आपकी पिछली कक्षाओं से आपको याद होगा कि एक बीजीय सर्वसमिका एक बीजीय समीकरण होता है जो उसमें आने वाले चरों के सभी मानों के लिए सत्य होता है। आपने पिछली कक्षाओं में निम्नलिखित बीजीय सर्वसमिकाएँ पढ़ी हैं:

सर्वसमिका I: $(x+y)^{2}=x^{2}+2 x y+y^{2}$

सर्वसमिका III: $(x-y)^{2}=x^{2}-2 x y+y^{2}$

सर्वसमिका III: $x^{2}-y^{2}=(x+y)(x-y)$

सर्वसमिका IV: $(x+a)(x+b)=x^{2}+(a+b) x+a b$

आपने इन बीजगणितीय सर्वसमिकाओं का उपयोग बीजगणितीय व्यंजकों का गुणनफल निकालने के लिए भी किया होगा। आप इनकी उपयोगिता संगणनाओं में भी देख सकते हैं।

उदाहरण 11 : उपयुक्त सर्वसमिकाओं का प्रयोग कर निम्नलिखित गुणनफल ज्ञात कीजिए:

(i) $(x+3)(x+3)$ $\quad$ (ii) $(x-3)(x+5)$

हल : (i) यहाँ हम सर्वसमिका I का उपयोग कर सकते हैं : $(x+y)^{2}=x^{2}+2 x y+y^{2}$। इसमें $y=3$ रखने पर, हम पाते हैं

$$ \begin{aligned} (x+3)(x+3) & =(x+3)^{2}=x^{2}+2(x)(3)+(3)^{2} \ & =x^{2}+6 x+9 \end{aligned} $$

(ii) ऊपर दी गई सर्वसमिका IV का उपयोग करते हुए, अर्थात् $(x+a)(x+b)=x^{2}+(a+b) x+a b$, हम पाते हैं

$$ \begin{aligned} (x-3)(x+5) & =x^{2}+(-3+5) x+(-3)(5) \ & =x^{2}+2 x-15 \end{aligned} $$

उदाहरण 12 : $105 \times 106$ का मान सीधे गुणा किए बिना ज्ञात कीजिए।

हल :

$$ \begin{aligned} 105 \times 106 & =(100+5) \times(100+6) \ & =(100)^{2}+(5+6)(100)+(5 \times 6), \text{ सर्वसमिका IV का उपयोग करते हुए } \ & =10000+1100+30 \ & =11130 \end{aligned} $$

आपने ऊपर सूचीबद्ध सर्वसमिकाओं के कुछ उपयोग दिए गए व्यंजकों के गुणनफल ज्ञात करने में देखे हैं। ये सर्वसमिकाएँ बीजगणितीय व्यंजकों के गुणनफल में भी उपयोगी होती हैं, जैसा कि आप निम्नलिखित उदाहरणों में देख सकते हैं।

उदाहरण 13 : गुणनफल ज्ञात कीजिए:

(i) $49 a^{2}+70 a b+25 b^{2}$

(ii) $\frac{25}{4} x^{2}-\frac{y^{2}}{9}$

हल : (i) यहाँ आप देख सकते हैं कि

$$49 a^{2}=(7 a)^{2}, 25 b^{2}=(5 b)^{2}, 70 a b=2(7 a)(5 b)$$

दिए गए व्यंजक की तुलना $x^{2}+2 x y+y^{2}$ से करने पर, हम देखते हैं कि $x=7 a$ और $y=5 b$ है।

पहचान I का प्रयोग करने पर हमें मिलता है $$ 49 a^{2}+70 a b+25 b^{2}=(7 a+5 b)^{2}=(7 a+5 b)(7 a+5 b) $$ (ii) हमारे पास $\frac{25}{4} x^{2}-\frac{y^{2}}{9}=\left(\frac{5}{2} x\right)^{2}-\left(\frac{y}{3}\right)^{2}$

अब इसकी तुलना पहचान III से करने पर हमें मिलता है

$$ \begin{aligned} \frac{25}{4} x^{2}-\frac{y^{2}}{9} & =\left(\frac{5}{2} x\right)^{2}-\left(\frac{y}{3}\right)^{2} \ & =\left(\frac{5}{2} x+\frac{y}{3}\right)\left(\frac{5}{2} x-\frac{y}{3}\right) \end{aligned} $$

अब तक, हमारी सभी पहचानों में द्विपदों के गुणनफल शामिल थे। आइए अब पहचान I को त्रिपद $x+y+z$ तक बढ़ाएँ। हम पहचान I का प्रयोग करके $(x+y+z)^{2}$ का परिकलन करेंगे।

मान लीजिए $x+y=t$. तब,

$$ \begin{aligned} (x+y+z)^{2} & =(t+z)^{2} \ & =t^{2}+2 t z+z^{2} \quad \text { (पहचान I का प्रयोग करते हुए) } \ & =(x+y)^{2}+2(x+y) z+z^{2} \quad(t \text { का मान रखने पर) } \ & =x^{2}+2 x y+y^{2}+2 x z+2 y z+z^{2} \quad \text { (पहचान I का प्रयोग करते हुए) } \ & =x^{2}+y^{2}+z^{2}+2 x y+2 y z+2 z x \text { (पदों को पुनः व्यवस्थित करने पर) } \end{aligned} $$

इस प्रकार, हमें निम्नलिखित पहचान प्राप्त होती है:

पहचान V : $(x+y+z)^{2}=x^{2}+y^{2}+z^{2}+2 x y+2 y z+2 z x$

टिप्पणी : हम दायें पक्ष के व्यंजक को बायें पक्ष के व्यंजक का विस्तारित रूप कहते हैं। ध्यान दें कि $(x+y+z)^{2}$ का विस्तार तीन वर्ग पदों और तीन गुणनफल पदों से मिलकर बनता है।

$$ \begin{aligned} & =x^{2}+2 x y+y^{2}+2 x z+2 y z+z^{2} \ & =x^{2}+y^{2}+z^{2}+2 x y+2 y z+2 z x \end{aligned} $$

उदाहरण 14 : $(3 a+4 b+5 c)^{2}$ को विस्तारित रूप में लिखिए।

हल: दिए गए व्यंजक की तुलना $(x+y+z)^{2}$ से करने पर, हम पाते हैं कि

$$ x=3 a, y=4 b \text{ और } z=5 c \text{।} $$

इसलिए, पहचान V का उपयोग करते हुए, हमारे पास

$$ \begin{aligned} (3 a+4 b+5 c)^{2} & =(3 a)^{2}+(4 b)^{2}+(5 c)^{2}+2(3 a)(4 b)+2(4 b)(5 c)+2(5 c)(3 a) \ & =9 a^{2}+16 b^{2}+25 c^{2}+24 a b+40 b c+30 a c \end{aligned} $$

उदाहरण 15: $(4 a-2 b-3 c)^{2}$ का विस्तार कीजिए।

हल: पहचान V का उपयोग करते हुए, हमारे पास

$$ \begin{aligned} (4 a-2 b-3 c)^{2} & =[4 a+(-2 b)+(-3 c)]^{2} \ & =(4 a)^{2}+(-2 b)^{2}+(-3 c)^{2}+2(4 a)(-2 b)+2(-2 b)(-3 c)+2(-3 c)(4 a) \ & =16 a^{2}+4 b^{2}+9 c^{2}-16 a b+12 b c-24 a c \end{aligned} $$

उदाहरण 16: $4 x^{2}+y^{2}+z^{2}-4 x y-2 y z+4 x z$ का गुणनफल ज्ञात कीजिए।

हल: हमारे पास $4 x^{2}+y^{2}+z^{2}-4 x y-2 y z+4 x z=(2 x)^{2}+(-y)^{2}+(z)^{2}+2(2 x)(-y)$

$$ +2(-y)(z)+2(2 x)(z) $$

$$ \begin{aligned} & =[2 x+(-y)+z]^{2} \quad \text{(पहचान V का उपयोग करते हुए)} \ & =(2 x-y+z)^{2}=(2 x-y+z)(2 x-y+z) \end{aligned} $$

अब तक, हमने द्वितीय घात के पदों वाली पहचानों से निपटा है। अब आइए पहचान I का विस्तार करके $(x+y)^{3}$ की गणना करें। हमारे पास:

$$ \begin{aligned} (x+y)^{3} & =(x+y)(x+y)^{2} \ & =(x+y)\left(x^{2}+2 x y+y^{2}\right) \ & =x\left(x^{2}+2 x y+y^{2}\right)+y\left(x^{2}+2 x y+y^{2}\right) \ & =x^{3}+2 x^{2} y+x y^{2}+x^{2} y+2 x y^{2}+y^{3} \ & =x^{3}+3 x^{2} y+3 x y^{2}+y^{3} \ & =x^{3}+y^{3}+3 x y(x+y) \end{aligned} $$

इसलिए, हमें निम्नलिखित पहचान मिलती है:

पहचान VI : $\quad(x+y)^{3}=x^{3}+y^{3}+3 x y(x+y)$

इसके अलावा, पहचान VI में $y$ को $-y$ से प्रतिस्थापित करने पर, हम प्राप्त करते हैं

पहचान VII : $(x-y)^{3}=x^{3}-y^{3}-3 x y(x-y)$ $=x^{3}-3 x^{2} y+3 x y^{2}-y^{3}$

उदाहरण 17 : निम्नलिखित घनों को विस्तारित रूप में लिखें:

(i) $(3 a+4 b)^{3}$ $\quad$ (ii) $(5 p-3 q)^{3}$

हल : (i) दिए गए व्यंजक की $(x+y)^{3}$ से तुलना करने पर, हम पाते हैं कि

$x=3 a \text { और } y=4 b \text {. }$

इसलिए, पहचान VI का उपयोग करते हुए, हमारे पास है:

$$ \begin{aligned} (3 a+4 b)^{3} & =(3 a)^{3}+(4 b)^{3}+3(3 a)(4 b)(3 a+4 b) \ & =27 a^{3}+64 b^{3}+108 a^{2} b+144 a b^{2} \end{aligned} $$

(ii) दिए गए व्यंजक की $(x-y)^{3}$ से तुलना करने पर, हम पाते हैं कि

$$x=5 p, y=3 q .$$

इसलिए, पहचान VII का उपयोग करते हुए, हमारे पास है:

$$ \begin{aligned} (5 p-3 q)^{3} & =(5 p)^{3}-(3 q)^{3}-3(5 p)(3 q)(5 p-3 q) \ & =125 p^{3}-27 q^{3}-225 p^{2} q+135 p q^{2} \end{aligned} $$

उदाहरण 18 : उपयुक्त पहचानों का उपयोग करके निम्नलिखित प्रत्येक का मूल्यांकन करें:

(i) $(104)^{3}$ (ii) $(999)^{3}$

हल: (i) हमारे पास है

$$ \begin{aligned} (104)^{3} & =(100+4)^{3} \ & =(100)^{3}+(4)^{3}+3(100)(4)(100+4) \ & \quad(\text{ पहचान VI का उपयोग करते हुए) } \ & =1000000+64+124800 \ & =1124864 \end{aligned} $$

(ii) हमारे पास है

$$ \begin{aligned} (999)^{3} & =(1000-1)^{3} \ & =(1000)^{3}-(1)^{3}-3(1000)(1)(1000-1) \ & \quad\text{ (पहचान VII का उपयोग करते हुए) } \ & =1000000000-1-2997000 \ & =997002999 \end{aligned} $$

उदाहरण 19 : गुणनखंड निकालें $8 x^{3}+27 y^{3}+36 x^{2} y+54 x y^{2}$

हल: दिए गए व्यंजक को इस प्रकार लिखा जा सकता है

$$ \begin{aligned} (2 x)^{3}+(3 y)^{3} & +3\left(4 x^{2}\right)(3 y)+3(2 x)\left(9 y^{2}\right) \ = & (2 x)^{3}+(3 y)^{3}+3(2 x)^{2}(3 y)+3(2 x)(3 y)^{2} \ = & (2 x+3 y)^{3} \quad(\text{पहचान VI का प्रयोग करते हुए)} \ = & (2 x+3 y)(2 x+3 y)(2 x+3 y) \ \end{aligned} $$

अब $(x+y+z)\left(x^{2}+y^{2}+z^{2}-x y-y z-z x\right)$ पर विचार करें
प्रसार करने पर, हमें गुणनफल प्राप्त होता है

$$ \begin{aligned} & x\left(x^{2}+y^{2}+z^{2}-x y-y z-z x\right)+y\left(x^{2}+y^{2}+z^{2}-x y-y z-z x\right) \ & +z\left(x^{2}+y^{2}+z^{2}-x y-y z-z x\right)=x^{3}+x y^{2}+x z^{2}-x^{2} y-x y z-z x^{2}+x^{2} y \ & +y^{3}+y z^{2}-x y^{2}-y^{2} z-x y z+x^{2} z+y^{2} z+z^{3}-x y z-y z^{2}-x z^{2} \ & =x^{3}+y^{3}+z^{3}-3 x y z \quad \text{(सरलीकरण पर)} \end{aligned} $$

इस प्रकार, हम निम्नलिखित पहचान प्राप्त करते हैं:

पहचान VIII: $x^{3}+y^{3}+z^{3}-3 x y z=(x+y+z)\left(x^{2}+y^{2}+z^{2}-x y-y z-z x\right)$

उदाहरण 20: गुणनखंड निकालें: $8 x^{3}+y^{3}+27 z^{3}-18 x y z$

हल: यहाँ, हमारे पास है

$$ \begin{aligned} 8 x^{3}+y^{3}+27 z^{3} & -18 x y z \ & =(2 x)^{3}+y^{3}+(3 z)^{3}-3(2 x)(y)(3 z) \ & =(2 x+y+3 z)\left[(2 x)^{2}+y^{2}+(3 z)^{2}-(2 x)(y)-(y)(3 z)-(2 x)(3 z)\right] \ & =(2 x+y+3 z)\left(4 x^{2}+y^{2}+9 z^{2}-2 x y-3 y z-6 x z\right)\ \end{aligned} $$

2.6 सारांश

इस अध्याय में, आपने निम्नलिखित बिंदुओं का अध्ययन किया है:

1. एक चर $x$ में एक बहुपद $p(x)$, $x$ के रूप में एक बीजगणितीय व्यंजक है जिसका रूप $p(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\ldots+a_{2} x^{2}+a_{1} x+a_{0}$ है, जहाँ $a_{0}, a_{1}, a_{2}, \ldots, a_{n}$ नियतांक हैं और $a_{n} \neq 0$ है।

$a_{0}, a_{1}, a_{2}, \ldots, a_{n}$ क्रमशः $x^{0}, x, x^{2}, \ldots, x^{n}$ के गुणांक हैं, और $n$ को बहुपद की घात कहा जाता है। $a_{n} x^{n}, a_{n-1} x^{n-1}, \ldots, a_{0}$ में से प्रत्येक, जहाँ $a_{n} \neq 0$ है, को बहुपद $p(x)$ का एक पद कहा जाता है।

2. एक पद वाले बहुपद को एकपदी (monomial) कहा जाता है।

3. दो पदों वाले बहुपद को द्विपद (binomial) कहा जाता है।

4. तीन पदों वाले बहुपद को त्रिपद (trinomial) कहा जाता है।

5. घात एक वाले बहुपद को रैखिक बहुपद (linear polynomial) कहा जाता है।

6. घात दो वाले बहुपद को द्विघात बहुपद (quadratic polynomial) कहा जाता है।

7. घात तीन वाले बहुपद को त्रिघात बहुपद (cubic polynomial) कहा जाता है।

8. एक वास्तविक संख्या ’ $a$ ’ बहुपद $p(x)$ का एक शून्यक (zero) है यदि $p(a)=0$। इस स्थिति में, $a$ को समीकरण $p(x)=0$ का एक मूल (root) भी कहा जाता है।

9. एक चर वाला प्रत्येक रैखिक बहुपद का एक अद्वितीय शून्यक होता है, एक अशून्य नियत बहुपद का कोई शून्यक नहीं होता, और प्रत्येक वास्तविक संख्या शून्य बहुपद का शून्यक होती है।

10. गुणनखंड प्रमेय (Factor Theorem) : यदि $p(a)=0$ है, तो $x-a$ बहुपद $p(x)$ का एक गुणनखंड है। इसके अतिरिक्त, यदि $x-a$ बहुपद $p(x)$ का एक गुणनखंड है, तो $p(a)=0$ होता है।

11. $(x+y+z)^{2}=x^{2}+y^{2}+z^{2}+2 x y+2 y z+2 z x$

12. $(x+y)^{3}=x^{3}+y^{3}+3 x y(x+y)$

13. $(x-y)^{3}=x^{3}-y^{3}-3 x y(x-y)$

१४. $x^{3}+y^{3}+z^{3}-3 x y z=(x+y+z)(x^{2}+y^{2}+z^{2}-x y-y z-z x)$