1.1 परिचय

आपने अपनी पिछली कक्षाओं में संख्या रेखा के बारे में सीखा है और इस पर विभिन्न प्रकार की संख्याओं को कैसे दर्शाया जाता है (देखिए चित्र 1.1)।

चित्र 1.1 : संख्या रेखा

बस कल्पना कीजिए कि आप शून्य से शुरू करते हैं और इस संख्या रेखा के साथ धनात्मक दिशा में चलते जाते हैं। जहाँ तक आपकी आँखें देख सकती हैं, वहाँ संख्याएँ ही संख्याएँ हैं!

चित्र 1.2

अब मान लीजिए आप संख्या रेखा के साथ चलना शुरू करते हैं और कुछ संख्याओं को इकट्ठा करते हैं। उन्हें रखने के लिए एक थैला तैयार कर लीजिए!

आप प्राकृतिक संख्याओं जैसे 1, 2, 3 आदि को उठाकर शुरुआत कर सकते हैं। आप जानते हैं कि यह सूची हमेशा के लिए चलती रहती है। (ऐसा क्यों है?) तो, अब आपके थैले में अनंत प्राकृतिक संख्याएँ हैं! याद कीजिए कि हम इस संग्रह को प्रतीक $\mathbf{N}$ से दर्शाते हैं।

अब मुड़ो और पूरे रास्ते वापस चलो, शून्य को उठाओ और थैले में डालो। अब तुम्हारे पास पूर्ण संख्याओं का संग्रह है जिसे प्रतीक $\mathbf{W}$ द्वारा दर्शाया जाता है।

अब तुम्हारे सामने बहुत-सी ऋणात्मक पूर्णांक फैली हैं। सभी ऋणात्मक पूर्णांकों को अपने थैले में डालो। तुम्हारा नया संग्रह क्या है? याद करो कि यह सभी पूर्णांकों का संग्रह है, और इसे प्रतीक $\mathbf{Z}$ द्वारा दर्शाया जाता है।

क्या रेखा पर अभी भी कुछ संख्याएँ बची हैं? बेशक! $\frac{1}{2}, \frac{3}{4}$, या यहाँ तक कि $\frac{-2005}{2006}$ जैसी संख्याएँ हैं। यदि तुम ऐसी सभी संख्याओं को भी थैले में डाल दो, तो यह अब परिमेय संख्याओं का संग्रह होगा।

परिमेय संख्याओं के संग्रह को $\mathbf{Q}$ द्वारा दर्शाया जाता है। ‘Rational’ शब्द ‘ratio’ से आया है, और Q शब्द ‘quotient’ से आया है।

तुम्हें परिमेय संख्याओं की परिभाषा याद होगी:

एक संख्या ’ $r$ ’ को एक परिमेय संख्या कहा जाता है, यदि इसे $\frac{p}{q}$ के रूप में लिखा जा सके, जहाँ $p$ और $q$ पूर्णांक हैं और $q \neq 0$। (हम यह क्यों ज़ोर देते हैं कि $q \neq 0$?)

ध्यान दीजिए कि अब थैले में सभी संख्याएँ $\frac{p}{q}$ के रूप में लिखी जा सकती हैं, जहाँ $p$ और $q$ पूर्णांक हैं और $q \neq 0$। उदाहरण के लिए, -25 को $\frac{-25}{1}$ के रूप में लिखा जा सकता है; यहाँ $p=-25$ और $q=1$ है। इसलिए, परिमेय संख्याओं में प्राकृत संख्याएँ, पूर्ण संख्याएँ और पूर्णांक भी शामिल होते हैं।
आप यह भी जानते हैं कि परिमेय संख्याओं की $\frac{p}{q}$ के रूप में अद्वितीय प्रस्तुति नहीं होती है, जहाँ $p$ और $q$ पूर्णांक हैं और $q \neq 0$। उदाहरण के लिए, $\frac{1}{2}=\frac{2}{4}=\frac{10}{20}=\frac{25}{50}$ $=\frac{47}{94}$, और इसी तरह। ये समतुल्य परिमेय संख्याएँ (या भिन्न) हैं। हालाँकि, जब हम कहते हैं कि $\frac{p}{q}$ एक परिमेय संख्या है, या जब हम $\frac{p}{q}$ को संख्या रेखा पर प्रस्तुत करते हैं, तो हम यह मान लेते हैं कि $q \neq 0$ और $p$ और $q$ में 1 के अतिरिक्त कोई उभयनिष्ठ गुणनखंड नहीं है (अर्थात्, $p$ और $q$ सह-अभाज्य हैं)। इसलिए, संख्या रेखा पर $\frac{1}{2}$ के अनंत समतुल्य भिन्नों में से, हम सभी को प्रस्तुत करने के लिए $\frac{1}{2}$ को चुनेंगे।

अब, आइए उन विभिन्न प्रकार की संख्याओं के कुछ उदाहरण हल करें, जिन्हें आपने पिछली कक्षाओं में पढ़ा है।

उदाहरण 1 : क्या निम्नलिखित कथन सत्य हैं या असत्य? अपने उत्तरों के कारण दीजिए।

(i) प्रत्येक पूर्ण संख्या एक प्राकृत संख्या है।

(ii) प्रत्येक पूर्णांक एक परिमेय संख्या है।

(iii) प्रत्येक परिमेय संख्या एक पूर्णांक है।

हल :(i) असत्य, क्योंकि शून्य एक पूर्ण संख्या है लेकिन एक प्राकृत संख्या नहीं है।

(ii) सत्य, क्योंकि प्रत्येक पूर्णांक $m$ को $\frac{m}{1}$ के रूप में व्यक्त किया जा सकता है, और इसलिए यह एक परिमेय संख्या है।(iii) असत्य, क्योंकि $\frac{3}{5}$ एक पूर्णांक नहीं है।

उदाहरण 2 : 1 और 2 के बीच पांच परिमेय संख्याएँ ज्ञात कीजिए।

हम इस समस्या को कम से कम दो तरीकों से हल कर सकते हैं।

हल 1 : याद कीजिए कि $r$ और $s$ के बीच एक परिमेय संख्या ज्ञात करने के लिए, आप $r$ और $s$ को जोड़ सकते हैं और योग को 2 से विभाजित कर सकते हैं, अर्थात् $\frac{r+s}{2}$, $r$ और $s$ के बीच स्थित होता है। इसलिए, $\frac{3}{2}$ एक संख्या है जो 1 और 2 के बीच है। आप इस तरह आगे बढ़ सकते हैं ताकि 1 और 2 के बीच चार और परिमेय संख्याएँ ज्ञात कर सकें। ये चार संख्याएँ $\frac{5}{4}, \frac{11}{8}, \frac{13}{8}$ और $\frac{7}{4}$ हैं।

हल 2 : दूसरा विकल्प यह है कि सभी पांच परिमेय संख्याओं को एक ही चरण में ज्ञात किया जाए। चूँकि हमें पाँच संख्याएँ चाहिए, हम 1 और 2 को हर $5+1$ वाली परिमेय संख्याओं के रूप में लिखते हैं, अर्थात् $1=\frac{6}{6}$ और $2=\frac{12}{6}$। फिर आप जाँच सकते हैं कि $\frac{7}{6}, \frac{8}{6}, \frac{9}{6}, \frac{10}{6}$ और $\frac{11}{6}$ सभी 1 और 2 के बीच की परिमेय संख्याएँ हैं। इसलिए, ये पाँच संख्याएँ $\frac{7}{6}, \frac{4}{3}, \frac{3}{2}, \frac{5}{3}$ और $\frac{11}{6}$ हैं।

टिप्पणी: ध्यान दीजिए कि उदाहरण 2 में आपसे 1 और 2 के बीच पाँच परिमेय संख्याएँ खोजने को कहा गया था। लेकिन, आपने अनुभव किया होगा कि वास्तव में 1 और 2 के बीच अनगिनत परिमेय संख्याएँ हैं। सामान्य तौर पर, किन्हीं भी दी गई दो परिमेय संख्याओं के बीच अनगिनत परिमेय संख्याएँ होती हैं।
आइए हम संख्या रेखा को फिर से देखें। क्या आपने सभी संख्याओं को उठा लिया है? अभी नहीं। सच तो यह है कि संख्या रेखा पर अनगिनत और संख्याएँ बची हुई हैं! जिन संख्याओं को आपने उठाया है, उनके बीच में खाली जगहें हैं, और वे एक-दो नहीं बल्कि अनगिनत हैं। आश्चर्यजनक बात यह है कि इन खाली जगहों में से किन्हीं भी दो के बीच भी अनगिनत संख्याएँ पड़ी हैं!

इसलिए हमारे पास निम्नलिखित प्रश्न बचे हैं:

1. संख्या रेखा पर जो संख्याएँ बची हैं, उन्हें क्या कहा जाता है?

2. हम उन्हें कैसे पहचानें? अर्थात्, हम उन्हें परिमेय संख्याओं से कैसे अलग करें?

इन प्रश्नों के उत्तर अगले खंड में दिए जाएँगे।

1.2 अपरिमेय संख्याएँ

हमने पिछले खंड में देखा कि संख्या रेखा पर ऐसी संख्याएँ हो सकती हैं जो परिमेय नहीं हैं। इस खंड में हम इन संख्याओं की जाँच करने जा रहे हैं। अब तक आपने जितनी भी संख्याएँ देखी हैं, वे सभी $\frac{p}{q}$ के रूप की हैं, जहाँ $p$ और $q$ पूर्णांक हैं और $q \neq 0$। तो आप पूछ सकते हैं: क्या ऐसी संख्याएँ हैं जो इस रूप की नहीं हैं? ऐसी संख्याएँ वास्तव में मौजूद हैं।

ग्रीस के पाइथागोरस के अनुयायी, प्रसिद्ध गणितज्ञ और दार्शनिक पाइथागोरस के अनुयायी, लगभग $400 \mathrm{BC}$ में पहले ऐसी संख्याओं की खोज करने वाले थे जो परिमेय नहीं थीं। इन संख्याओं को अपरिमेय संख्याएँ (irrational numbers) कहा जाता है, क्योंकि इन्हें पूर्णांकों के अनुपात के रूप में नहीं लिखा जा सकता। पाइथागोरस के अनुयायी, क्रोटोन के हिप्पाकस द्वारा अपरिमेय संख्याओं की खोज को लेकर कई मिथक हैं। सभी मिथकों में हिप्पाकस का अंत दुर्भाग्यपूर्ण होता है, चाहे वह $\sqrt{2}$ के अपरिमेय होने की खोज के कारण हो या पाइथागोरस गुप्त संप्रदाय के बाहर के लोगों को $\sqrt{2}$ के बारे में रहस्य प्रकट करने के कारण!

पाइथागोरस

(569 BCE - 479 BCE)

चित्र 1.3

आइए इन संख्याओं को औपचारिक रूप से परिभाषित करें।

एक संख्या ‘$\mathrm{s}$’ को अपरिमेय कहा जाता है, यदि उसे $\frac{p}{q}$ के रूप में नहीं लिखा जा सकता, जहाँ $p$ और $q$ पूर्णांक हैं और $q \neq 0$।

आप पहले से जानते हैं कि परिमेय संख्याएँ अनंत हैं। यह पता चलता है कि अपरिमेय संख्याएँ भी अनंत हैं। कुछ उदाहरण हैं:

$$ \sqrt{2}, \sqrt{3}, \sqrt{15}, \pi, 0.10110111011110 \ldots $$

टिप्पणी : याद कीजिए कि जब हम प्रतीक $\sqrt{ }$ का प्रयोग करते हैं, तो हम मान लेते हैं कि यह संख्या का धनात्मक वर्गमूल है। इसलिए $\sqrt{4}=2$, यद्यपि 2 और -2 दोनों ही 4 के वर्गमूल हैं।

ऊपर सूचीबद्ध कुछ अपरिमेय संख्याएँ आपको परिचित हैं। उदाहरण के लिए, आप पहले ही ऊपर दी गई कई वर्गमूल संख्याओं और संख्या $\pi$ के बारे में पढ़ चुके हैं।

पाइथागोरस ने सिद्ध किया कि $\sqrt{2}$ अपरिमेय है। बाद में लगभग $425 \mathrm{BC}$ में, सायरीन के थियोडोरस ने दिखाया कि $\sqrt{3}, \sqrt{5}, \sqrt{6}, \sqrt{7}, \sqrt{10}, \sqrt{11}, \sqrt{12}, \sqrt{13}, \sqrt{14}, \sqrt{15}$ और $\sqrt{17}$ भी अपरिमेय हैं। $\sqrt{2}, \sqrt{3}, \sqrt{5}$, आदि की अपरिमेयता के प्रमाण कक्षा X में चर्चा किए जाएँगे। जहाँ तक $\pi$ की बात है, यह हजारों वर्षों से विभिन्न संस्कृतियों को ज्ञात था, लेकिन इसे लैम्बर्ट और लेजेंड्रे ने केवल $1700$ के दशक के अंत में अपरिमेय सिद्ध किया। अगले खंड में, हम चर्चा करेंगे कि $0.10110111011110 \ldots$ और $\pi$ अपरिमेय क्यों हैं।

आइए पिछले खंड के अंत में उठाए गए प्रश्नों पर लौटते हैं। याद कीजिए परिमेय संख्याओं का थैला। यदि हम अब उस थैले में सभी अपरिमेय संख्याएँ भी डाल दें, तो क्या संख्या रेखा पर कोई संख्या बचेगी? उत्तर है—नहीं! यह पता चलता है कि सभी परिमेय संख्याओं और अपरिमेय संख्याओं का संग्रह मिलकर वह संग्रह बनाता है जिसे हम वास्तविक संख्याओं का संग्रह कहते हैं,

जिसे $\mathbf{R}$ द्वारा निरूपित किया जाता है। इसलिए, एक वास्तविक संख्या या तो परिमेय होती है या अपरिमेय। इस प्रकार, हम कह सकते हैं कि प्रत्येक वास्तविक संख्या संख्या रेखा पर एक अद्वितीय बिंदु द्वारा निरूपित की जाती है। साथ ही, संख्या रेखा पर प्रत्येक बिंदु एक अद्वितीय वास्तविक संख्या को निरूपित करता है। यही कारण है कि हम संख्या रेखा को वास्तविक संख्या रेखा कहते हैं।

आर. डिडेकिंड (1831-1916)

चित्र 1.4

1870 के दशक में दो जर्मन गणितज्ञ, कैंटर और डिडेकिंड, ने दिखाया कि: हर वास्तविक संख्या के अनुरूप वास्तविक संख्या रेखा पर एक बिंदु होता है, और संख्या रेखा के हर बिंदु के अनुरूप एक अद्वितीय वास्तविक संख्या मौजूद होती है।

जी. कैंटर (1845-1918) चित्र 1.5

आइए देखें कि हम कुछ अपरिमेय संख्याओं को संख्या रेखा पर कैसे स्थित कर सकते हैं।

उदाहरण 3 : $\sqrt{2}$ को संख्या रेखा पर स्थित कीजिए।

हल : यह देखना आसान है कि ग्रीक लोगों ने $\sqrt{2}$ की खोज कैसे की होगी। एक वर्ग $\mathrm{OABC}$ पर विचार कीजिए, जिसकी प्रत्येक भुजा की लंबाई 1 इकाई है (चित्र 1.6 देखें)। फिर आप पाइथागोरस प्रमेय से देख सकते हैं कि $\mathrm{OB}=\sqrt{1^{2}+1^{2}}=\sqrt{2}$। हम $\sqrt{2}$ को संख्या रेखा पर कैसे दर्शाते हैं?

चित्र 1.6 यह आसान है। चित्र 1.6 को संख्या रेखा पर स्थानांतरित करें यह सुनिश्चित करते हुए कि शीर्ष बिंदु (\mathrm{O}) शून्य के साथ मेल खाता है (देखें चित्र 1.7)।

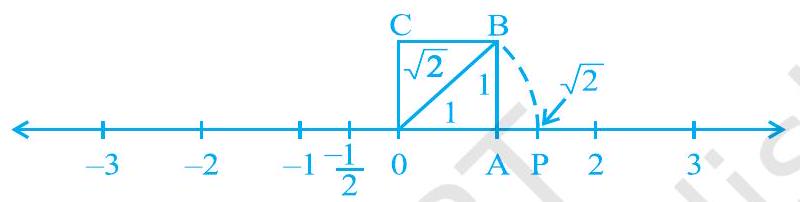
चित्र 1.7

हमने अभी देखा है कि (\mathrm{OB}=\sqrt{2})। एक परकार का प्रयोग करते हुए केंद्र (\mathrm{O}) और त्रिज्या (\mathrm{OB}) से एक चाप खींचें जो संख्या रेखा को बिंदु (P) पर काटता है। तब (P) संख्या रेखा पर (\sqrt{2}) के अनुरूप होगा।

उदाहरण 4 : संख्या रेखा पर (\sqrt{3}) को स्थित करें।

हल : आइए चित्र 1.7 पर वापस लौटें।

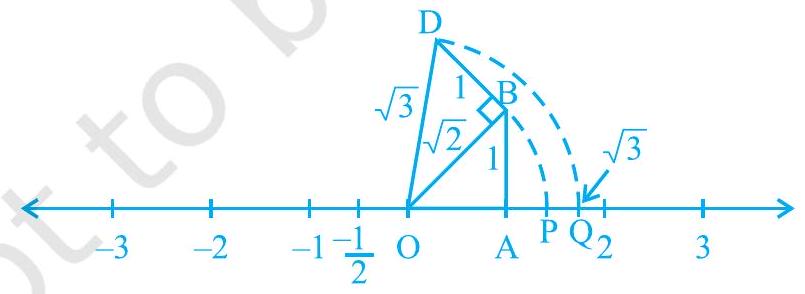
चित्र 1.8

(\mathrm{OB}) पर लंबवत इकाई लंबाई की (\mathrm{BD}) रचित करें (जैसा कि चित्र 1.8 में है)। तब पाइथागोरस प्रमेय का प्रयोग करते हुए, हम देखते हैं कि (\mathrm{OD}=\sqrt{(\sqrt{2})^{2}+1^{2}}=\sqrt{3})। एक परकार का प्रयोग करते हुए, केंद्र (\mathrm{O}) और त्रिज्या (\mathrm{OD}) से एक चाप खींचें जो संख्या रेखा को बिंदु (\mathrm{Q}) पर काटता है। तब (\mathrm{Q}) संख्या रेखा पर (\sqrt{3}) के अनुरूप होगा।

इसी प्रकार, आप किसी भी धनात्मक पूर्णांक (n) के लिए (\sqrt{n}) को स्थित कर सकते हैं, बशर्ते (\sqrt{n-1}) पहले स्थित किया जा चुका हो।

1.3 वास्तविक संख्याएँ और उनके दशमलव विस्तार

इस खंड में, हम परिमेय और अपरिमेय संख्याओं को एक अलग दृष्टिकोण से अध्ययन करने जा रहे हैं। हम वास्तविक संख्याओं के दशमलव प्रसार को देखेंगे और देखेंगे कि क्या हम इन प्रसारों का उपयोग परिमेय और अपरिमेय संख्याओं के बीच अंतर करने के लिए कर सकते हैं। हम यह भी समझाएंगे कि दशमलव प्रसारों का उपयोग करके संख्या रेखा पर वास्तविक संख्याओं के प्रतिनिधित्व को कैसे देखा जा सकता है। चूंकि परिमेय संख्याएं हमें अधिक परिचित हैं, आइए उनसे शुरुआत करें। आइए तीन उदाहरण लें: $\frac{10}{3}, \frac{7}{8}, \frac{1}{7}$।
शेषों पर विशेष ध्यान दें और देखें कि क्या आप कोई प्रतिरूप पा सकते हैं।

उदाहरण 5 : $\frac{10}{3}, \frac{7}{8}$ और $\frac{1}{7}$ के दशमलव प्रसार ज्ञात कीजिए।

हल :

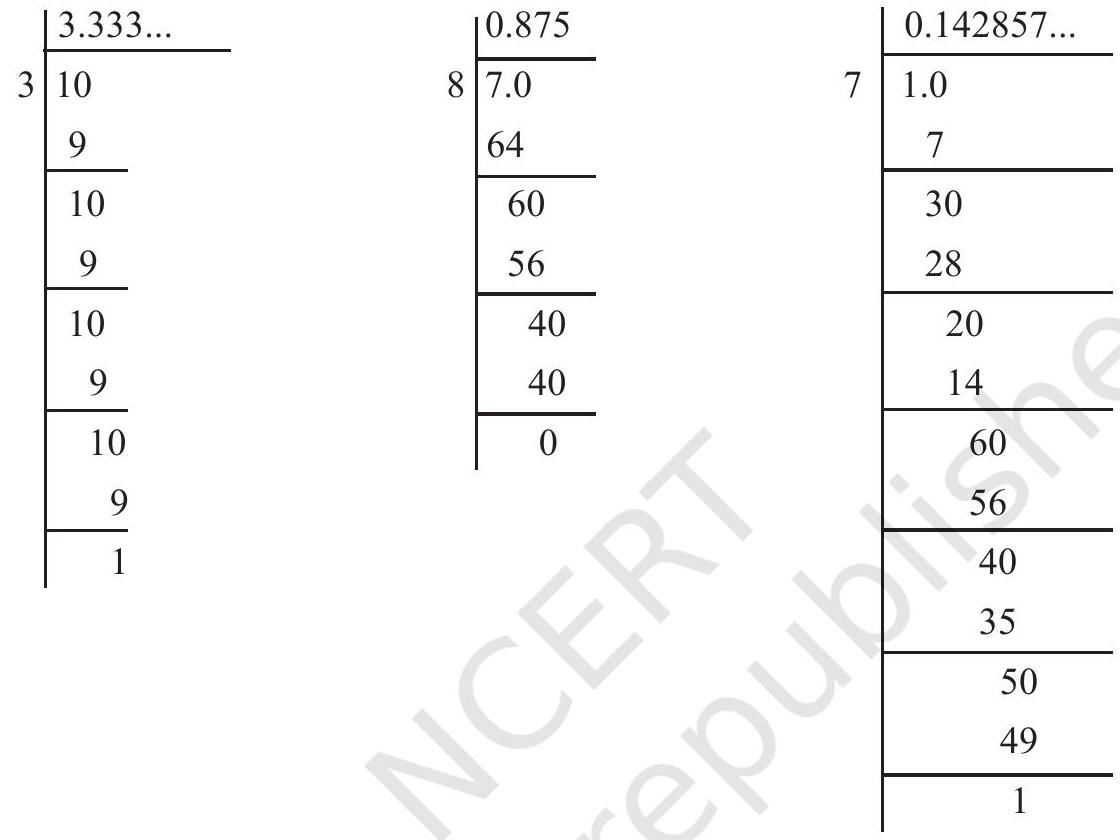
शेष : $1,1,1,1,1 \ldots$ भाजक : 3

शेष : $6,4,0$ भाजक : 8
शेष : $3,2,6,4,5,1$, $3,2,6,4,5,1, \ldots$

भाजक : 7

आपने क्या देखा? आपने कम से कम तीन बातें देखी होंगी:

(i) शेष या तो एक निश्चित चरण के बाद 0 हो जाते हैं, या फिर वे दोहरने लगते हैं।

(ii) शेषों की दोहराने वाली श्रृंखला में प्रविष्टियों की संख्या भाजक से कम होती है ($\frac{10}{3}$ में एक संख्या दोहराती है और भाजक 3 है, $\frac{1}{7}$ में शेषों की दोहराने वाली श्रृंखला में 326451 छह प्रविष्टियाँ हैं और भाजक 7 है)।

(iii) यदि शेषफल दोहराने लगें, तो भागफल में अंकों की एक दोहराती ब्लॉक मिलती है ($\frac{10}{3}$ के लिए 3 भागफल में दोहराता है और $\frac{1}{7}$ के लिए हमें भागफल में दोहराती ब्लॉक 142857 मिलती है)।

यद्यपि हमने इस प्रतिरूप को केवल उपरोक्त उदाहरणों का उपयोग करके देखा है, यह सभी $\frac{p}{q}(q \neq 0)$ रूप के परिमेय संख्याओं के लिए सत्य है। $p$ को $q$ से भाग देने पर दो मुख्य चीज़ें होती हैं—या तो शेषफल शून्य हो जाता है या कभी शून्य नहीं होता और हमें शेषफलों की एक दोहराती श्रृंखला मिलती है। आइए प्रत्येक स्थिति को अलग-अलग देखें।

स्थिति (i) : शेषफल शून्य हो जाता है

$\frac{7}{8}$ के उदाहरण में, हमने पाया कि कुछ चरणों के बाद शेषफल शून्य हो जाता है और $\frac{7}{8}=0.875$ का दशमलव प्रसार होता है। अन्य उदाहरण हैं $\frac{1}{2}=0.5$, $\frac{639}{250}=2.556$। इन सभी स्थितियों में दशमलव प्रसार समाप्त हो जाता है या सीमित संख्या में चरणों के बाद समाप्त हो जाता है। हम ऐसी संख्याओं के दशमलव प्रसार को सांत कहते हैं।

स्थिति (ii) : शेषफल कभी शून्य नहीं होता

$\frac{10}{3}$ और $\frac{1}{7}$ के उदाहरणों में, हम देखते हैं कि एक निश्चित चरण के बाद शेषफल दोहराने लगते हैं, जिससे दशमलव प्रसार सदा के लिए चलता रहता है। दूसरे शब्दों में, भागफल में अंकों की एक दोहराती ब्लॉक होती है। हम कहते हैं कि यह प्रसार असांत आवर्ती है। उदाहरण के लिए, $\frac{10}{3}=3.3333 \ldots$ और $\frac{1}{7}=0.142857142857142857 \ldots$

3 को $\frac{10}{3}$ के भागफल में दोहराता दिखाने का सामान्य तरीका इसे $3 . \overline{3}$ के रूप में लिखना है। इसी तरह, चूँकि अंकों का ब्लॉक 142857, $\frac{1}{7}$ के भागफल में दोहराता है, हम $\frac{1}{7}$ को $0 . \overline{142857}$ लिखते हैं, जहाँ अंकों के ऊपर की पट्टी दोहराते अंकों के ब्लॉक को दर्शाती है। साथ ही 3.57272… को $3.5 \overline{72}$ लिखा जा सकता है। इसलिए, ये सभी उदाहरण हमें गैर-समाप्त आवर्ती (दोहराते) दशमलव विस्तार देते हैं।

इस प्रकार, हम देखते हैं कि परिमेय संख्याओं का दशमलव विस्तार केवल दो विकल्पों में होता है: या तो वे समाप्त होते हैं या गैर-समाप्त आवर्ती होते हैं।

अब मान लीजिए, दूसरी ओर, संख्या रेखा पर आपकी चलते हुए, आपको 3.142678 जैसी कोई संख्या मिलती है जिसका दशमलव विस्तार समाप्त होता है या $1.272727 \ldots$ यानी $1 . \overline{27}$ जैसी संख्या मिलती है, जिसका दशमलव विस्तार गैर-समाप्त आवर्ती है, क्या आप निष्कर्ष निकाल सकते हैं कि यह एक परिमेय संख्या है? उत्तर है हाँ!

हम इसे सिद्ध नहीं करेंगे बल्कि कुछ उदाहरणों के साथ इस तथ्य को दर्शाएँगे। समाप्त होने वाले मामले आसान होते हैं।

उदाहरण 6 : दिखाइए कि 3.142678 एक परिमेय संख्या है। दूसरे शब्दों में, 3.142678 को $\frac{p}{q}$ के रूप में व्यक्त करें, जहाँ $p$ और $q$ पूर्णांक हैं और $q \neq 0$।

हल : हमारे पास $3.142678=\frac{3142678}{1000000}$ है, और इसलिए यह एक परिमेय संख्या है।

अब, आइए उस स्थिति पर विचार करें जब दशमलव विस्तार गैर-समाप्त आवर्ती हो।

उदाहरण 7 : दिखाइए कि $0.3333 \ldots=0 . \overline{3}$ को $\frac{p}{q}$ के रूप में व्यक्त किया जा सकता है, जहाँ $p$ और $q$ पूर्णांक हैं और $q \neq 0$।

हल : चूँकि हम नहीं जानते कि $0 . \overline{3}$ क्या है, आइए हम इसे ’ $x$ ’ कहें और इसलिए

$$ x=0.3333 \ldots $$

अब यहाँ वह चाल आती है। देखिए अब,

$$ 10 x=10 \times(0.333 \ldots)=3.333 \ldots $$

$$ 3.3333 \ldots=3+x \text{, चूँकि } x=0.3333 \ldots $$

इसलिए,

$$ 10 x=3+x $$

$x$ के लिए हल करने पर, हमें मिलता है

$$ 9 x=3 \text{, अर्थात्, } x=\frac{1}{3} $$

उदाहरण 8 : दिखाइए कि $1.272727 \ldots=1 . \overline{27}$ को $\frac{p}{q}$ के रूप में व्यक्त किया जा सकता है, जहाँ $p$ और $q$ पूर्णांक हैं और $q \neq 0$।

हल : मान लीजिए $x=1.272727 \ldots$ चूँकि दो अंक दोहरा रहे हैं, हम $x$ को 100 से गुणा करते हैं

इसलिए, $$ 100 x=127.2727 \ldots $$

इसलिए,

$$ 100 x=126+1.272727 \ldots=126+x $$

$$100 x-x=126$, अर्थात्, $99 x=126$$

अर्थात्, $$ x=\frac{126}{99}=\frac{14}{11} $$

आप उल्टे की जाँच कर सकते हैं कि $\frac{14}{11}=1 . \overline{27}$।

उदाहरण 9 : दिखाइए कि $0.2353535 \ldots=0.2 \overline{35}$ को $\frac{p}{q}$ के रूप में व्यक्त किया जा सकता है, जहाँ $p$ और $q$ पूर्णांक हैं और $q \neq 0$।

हल : मान लीजिए $x=0.2 \overline{35}$। यहाँ, ध्यान दें कि 2 दोहरा नहीं रहा है, लेकिन ब्लॉक 35 दोहरा रहा है। चूँकि दो अंक दोहरा रहे हैं, हम $x$ को 100 से गुणा करते हैं

$$ \begin{aligned} 100 x & =23.53535 \ldots \ 100 x & =23.3+0.23535 \ldots=23.3+x \ 99 x & =23.3 \end{aligned} $$

इसलिए,
अतः,
अर्थात्,
$$ 99 x=\frac{233}{10}, \text { जिससे } x=\frac{233}{990} $$

आप इसका उल्टा भी जाँच सकते हैं कि $\frac{233}{990}=0.2 \overline{35}$

इसलिए, हर वह संख्या जिसका दशमलव प्रसार असमापी आवर्ती है, $\frac{p}{q}(q \neq 0)$ के रूप में व्यक्त की जा सकती है, जहाँ $p$ और $q$ पूर्णांक हैं। आइए अपने परिणामों को निम्नलिखित रूप में संक्षेप में प्रस्तुत करें :

एक परिमेय संख्या का दशमलव प्रसार या तो समाप्त होता है या असमापी आवर्ती होता है। इसके अतिरिक्त, एक संख्या जिसका दशमलव प्रसार समाप्त होता है या असमापी आवर्ती होता है, परिमेय होती है।

इसलिए, अब हम जानते हैं कि एक परिमेय संख्या का दशमलव प्रसार क्या हो सकता है। क्या आपने कभी सोचा है कि अपरिमेय संख्याओं का दशमलव प्रसार कैसा होता है? उपरोक्त गुणधर्म के कारण, हम यह निष्कर्ष निकाल सकते हैं कि उनका दशमलव प्रसार असमापी और अनावर्ती होता है। इसलिए, अपरिमेय संख्याओं के लिए गुणधर्म, जो परिमेय संख्याओं के लिए उपरोक्त गुणधर्म के समान है, यह है :

एक अपरिमेय संख्या का दशमलव प्रसार असमापी अनावर्ती होता है। इसके अतिरिक्त, एक संख्या जिसका दशमलव प्रसार असमापी अनावर्ती होता है, अपरिमेय होती है।

पिछले खंड से $s=0.10110111011110 \ldots$ को याद कीजिए। ध्यान दीजिए कि यह असमापी और अनावर्ती है। इसलिए, उपरोक्त गुणधर्म से, यह अपरिमेय है। इसके अतिरिक्त, ध्यान दीजिए कि आप $s$ के समान अनंत अपरिमेय संख्याएँ उत्पन्न कर सकते हैं।

प्रसिद्ध अपरिमेय संख्याओं $\sqrt{2}$ और $\pi$ का क्या? यहाँ उनके दशमलव प्रसार किसी निश्चित स्तर तक दिए गए हैं।

$$ \begin{aligned} \sqrt{2} & =1.4142135623730950488016887242096 \ldots \\ \pi & =3.14159265358979323846264338327950 \ldots \end{aligned} $$

(ध्यान दें कि हम अक्सर $\pi$ का एक अनुमानित मान $\frac{22}{7}$ लेते हैं, लेकिन $\pi \neq \frac{22}{7}$।)

वर्षों से, गणितज्ञों ने अपरिमेय संख्याओं की दशमलव विस्तार में अधिक से अधिक अंक उत्पन्न करने की विभिन्न तकनीकें विकसित की हैं। उदाहरण के लिए, आपने विभाजन विधि द्वारा $\sqrt{2}$ के दशमलव विस्तार में अंक खोजना सीखा होगा। रोचक बात यह है कि सुल्बसूत्रों (जोड़ के नियम) में, वैदिक काल (800 ई.पू. - 500 ई.पू.) की एक गणितीय ग्रंथ, आप $\sqrt{2}$ का एक अनुमान इस प्रकार पाते हैं:

$$ \sqrt{2}=1+\frac{1}{3}+\left(\frac{1}{4} \times \frac{1}{3}\right)-\left(\frac{1}{34} \times \frac{1}{4} \times \frac{1}{3}\right)=1.4142156 $$

ध्यान दें कि यह ऊपर दिए गए मान के पहले पाँच दशमलव स्थानों तक समान है। $\pi$ के दशमलव विस्तार में अंकों की खोज का इतिहास बहुत रोचक है।

ग्रीक प्रतिभाशाली आर्किमिडीज़ ने $\pi$ के दशमलव विस्तार के अंकों की गणना करने वाले पहले व्यक्ति थे। उन्होंने दिखाया कि 3.140845 $<\pi<3.142857$। आर्यभट्ट (476-550 ई.स.), महान भारतीय गणितज्ञ और खगोलशास्त्री, ने $\pi$ का मान चार दशमलव स्थानों तक सही (3.1416) निकाला। उच्च गति के कंप्यूटरों और उन्नत एल्गोरिदमों का उपयोग करके, $\pi$ को 1.24 ट्रिलियन दशमलव स्थानों तक गणना किया गया है!

आर्किमिडीज़ (287 ईसा पूर्व-212 ईसा पूर्व)

चित्र 1.10

अब, आइए देखें कि अपरिमेय संख्याओं को कैसे प्राप्त किया जाए।

उदाहरण 10 : $\frac{1}{7}$ और $\frac{2}{7}$ के बीच एक अपरिमेय संख्या ज्ञात कीजिए।

हल : हमने देखा कि $\frac{1}{7}=0 . \overline{142857}$। इसलिए, आप आसानी से $\frac{2}{7}=0 . \overline{285714}$ की गणना कर सकते हैं।

$\frac{1}{7}$ और $\frac{2}{7}$ के बीच एक अपरिमेय संख्या खोजने के लिए, हम एक ऐसी संख्या खोजते हैं जि सका दशमलव प्रसार असांत और अनावर्ती हो और वह इन दोनों के बीच में हो। निश्चित रूप से, आप ऐसी अनंत संख्याएँ खोज सकते हैं।

ऐसी संख्या का एक उदाहरण है $0.150150015000150000 \ldots$

1.4 वास्तविक संख्याओं पर संक्रियाएँ

आपने पिछली कक्षाओं में सीखा है कि परिमेय संख्याएँ योग और गुणा के लिए क्रमविनिमेय, साहचर्य और वितरण नियमों को संतुष्ट करती हैं। इसके अलावा, यदि हम दो परिमेय संख्याओं को जोड़ें, घटाएँ, गुणा करें या विभाजित करें (शून्य को छोड़कर), तो हमें अभी भी एक परिमेय संख्या प्राप्त होती है (अर्थात्, परिमेय संख्याएँ योग, घटाव, गुणा और विभाजन के सापेक्ष ‘बंद’ हैं)। यह पता चलता है कि अपरिमेय संख्याएँ भी योग और गुणा के लिए क्रमविनिमेय, साहचर्य और वितरण नियमों को संतुष्ट करती हैं। हालाँकि, अपरिमेय संख्याओं के योग, अंतर, भागफल और गुणनफल हमेशा अपरिमेय नहीं होते। उदाहरण के लिए, $(\sqrt{6})+(-\sqrt{6}),(\sqrt{2})-(\sqrt{2}),(\sqrt{3}) \cdot(\sqrt{3})$ और $\frac{\sqrt{17}}{\sqrt{17}}$ परिमेय हैं।

आइए देखें कि जब हम एक परिमेय संख्या को किसी अपरिमेय संख्या के साथ जोड़ते या गुणा करते हैं तो क्या होता है। उदाहरण के लिए, $\sqrt{3}$ अपरिमेय है। $2+\sqrt{3}$ और $2 \sqrt{3}$ के बारे में क्या? चूँकि $\sqrt{3}$ का दशमलव विस्तार अनवसानी और अनावर्ती है, वही $2+\sqrt{3}$ और $2 \sqrt{3}$ के लिए भी सत्य है। इसलिए, $2+\sqrt{3}$ और $2 \sqrt{3}$ दोनों भी अपरिमेय संख्याएँ हैं।

उदाहरण 11 : जाँच कीजिए कि $7 \sqrt{5}, \frac{7}{\sqrt{5}}, \sqrt{2}+21, \pi-2$ अपरिमेय संख्याएँ हैं या नहीं।

हल : $\sqrt{5}=2.236 \ldots, \sqrt{2}=1.4142 \ldots, \pi=3.1415 \ldots$

तब $7 \sqrt{5}=15.652 \ldots, \frac{7}{\sqrt{5}}=\frac{7 \sqrt{5}}{\sqrt{5} \sqrt{5}}=\frac{7 \sqrt{5}}{5}=3.1304 \ldots$

$\sqrt{2}+21=22.4142 \ldots, \pi-2=1.1415 \ldots$

ये सभी अनवसानी अनावर्ती दशमलव हैं। इसलिए, ये सभी अपरिमेय संख्याएँ हैं।

उदाहरण 12 : $2 \sqrt{2}+5 \sqrt{3}$ और $\sqrt{2}-3 \sqrt{3}$ को जोड़ें।

हल : $(2 \sqrt{2}+5 \sqrt{3})+(\sqrt{2}-3 \sqrt{3})=(2 \sqrt{2}+\sqrt{2})+(5 \sqrt{3}-3 \sqrt{3})$

$=(2+1) \sqrt{2}+(5-3) \sqrt{3}=3 \sqrt{2}+2 \sqrt{3}$

उदाहरण 13 : $6 \sqrt{5}$ को $2 \sqrt{5}$ से गुणा करें।

हल : $6 \sqrt{5} \times 2 \sqrt{5}=6 \times 2 \times \sqrt{5} \times \sqrt{5}=12 \times 5=60$

उदाहरण 14 : $8 \sqrt{15}$ को $2 \sqrt{3}$ से विभाजित करें।

हल : $8 \sqrt{15} \div 2 \sqrt{3}=\frac{8 \sqrt{3} \times \sqrt{5}}{2 \sqrt{3}}=4 \sqrt{5}$

ये उदाहरण आपको निम्नलिखित तथ्यों की ओर संकेत कर सकते हैं, जो सत्य हैं:

(i) एक परिमेय संख्या और एक अपरिमेय संख्या का योग या अंतर अपरिमेय होता है।

(ii) एक अशून्य परिमेय संख्या और एक अपरिमेय संख्या का गुणनफल या भागफल अपरिमेय होता है।

(iii) यदि हम दो अपरिमेय संख्याओं को जोड़ें, घटाएँ, गुणा करें या विभाजित करें, तो परिणाम परिमेय या अपरिमेय हो सकता है।

अब हम वास्तविक संख्याओं के वर्गमूल निकालने की संक्रिया की ओर ध्यान देते हैं। याद कीजिए, यदि $a$ एक प्राकृत संख्या है, तो $\sqrt{a}=b$ का अर्थ है $b^{2}=a$ और $b>0$। वही परिभाषा धनात्मक वास्तविक संख्याओं के लिए भी बढ़ाई जा सकती है।

मान लीजिए $a>0$ एक वास्तविक संख्या है। तब $\sqrt{a}=b$ का अर्थ है $b^{2}=a$ और $b>0$।

अनुच्छेद 1.2 में, हमने देखा कि किसी भी धनात्मक पूर्णांक $n$ के लिए $\sqrt{n}$ को संख्या रेखा पर कैसे दर्शाया जाता है। अब हम यह दिखाते हैं कि किसी दिए गए धनात्मक वास्तविक संख्या $x$ के लिए $\sqrt{x}$ को ज्यामितीय रूप से कैसे ज्ञात किया जाए।
उदाहरण के लिए, आइए इसे $x=3.5$ के लिए ज्ञात करें, अर्थात् हम $\sqrt{3.5}$ को ज्यामितीय रूप से ज्ञात करते हैं।

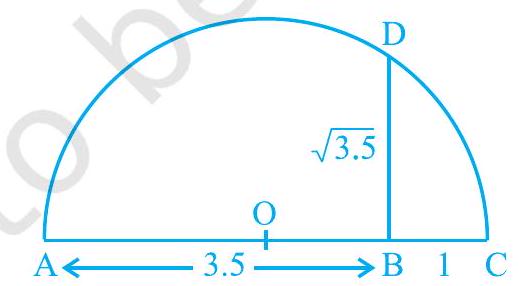
आकृति 1.11

एक दी गई रेखा पर एक निश्चित बिंदु $\mathrm{A}$ से 3.5 इकाई की दूरी चिह्नित करें ताकि एक बिंदु $\mathrm{B}$ प्राप्त हो जिससे $AB = 3.5$ इकाई हो (देखें आकृति 1.11)। $\mathrm{B}$ से 1 इकाई की दूरी चिह्नित करें और नए बिंदु को $\mathrm{C}$ चिह्नित करें। $\mathrm{AC}$ का मध्य-बिंदु ज्ञात करें और उस बिंदु को $\mathrm{O}$ चिह्नित करें। $\mathrm{O}$ को केंद्र और $\mathrm{OC}$ को त्रिज्या लेकर एक अर्धवृत्त खींचें। $\mathrm{AC}$ पर लंब एक रेखा खींचें जो $\mathrm{B}$ से गुजरे और अर्धवृत्त को $\mathrm{D}$ पर काटे। तब, $\mathrm{BD} = \sqrt{3.5}$।

अधिक सामान्य रूप से, किसी भी धनात्मक वास्तविक संख्या $x$ के लिए $\sqrt{x}$ ज्ञात करने के लिए, हम $\mathrm{B}$ को इस प्रकार चिह्नित करते हैं कि $\mathrm{AB} = x$ इकाई हो, और, जैसा कि आकृति 1.12 में दिखाया गया है, $\mathrm{C}$ को इस प्रकार चिह्नित करते हैं कि $\mathrm{BC} = 1$ इकाई हो। फिर, जैसा कि हमने $x = 3.5$ के मामले में किया है, हम $\mathrm{BD} = \sqrt{x}$ प्राप्त करते हैं (देखें आकृति 1.12)। हम इस परिणाम को पाइथागोरस प्रमेय का उपयोग करके सिद्ध कर सकते हैं।

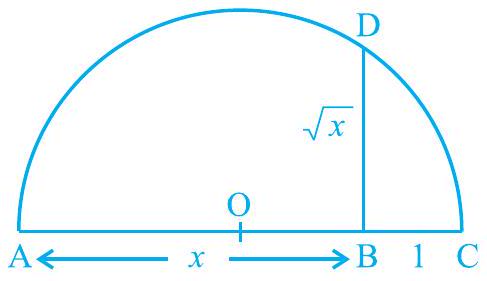
चित्र 1.12

ध्यान दें कि, चित्र 1.12 में, $\Delta \mathrm{OBD}$ एक समकोण त्रिभुज है। साथ ही, वृत्त की त्रिज्या $\frac{x+1}{2}$ इकाई है।

इसलिए, $\mathrm{OC}=\mathrm{OD}=\mathrm{OA}=\frac{x+1}{2}$ इकाई।

अब, $\mathrm{OB}=x-\left(\frac{x+1}{2}\right)=\frac{x-1}{2}$।

अतः, पाइथागोरस प्रमेय से, हमें प्राप्त होता है

$$ \mathrm{BD}^{2}=\mathrm{OD}^{2}-\mathrm{OB}^{2}=\left(\frac{x+1}{2}\right)^{2}-\left(\frac{x-1}{2}\right)^{2}=\frac{4 x}{4}=x $$

यह दर्शाता है कि $\mathrm{BD}=\sqrt{x}$।

यह रचना हमें एक दृश्यात्मक और ज्यामितीय तरीका देती है यह दिखाने के लिए कि सभी वास्तविक संख्याओं $x>0$ के लिए $\sqrt{x}$ का अस्तित्व है। यदि आप जानना चाहते हैं कि $\sqrt{x}$ संख्या रेखा पर कहाँ स्थित है, तो आइए रेखा $\mathrm{BC}$ को संख्या रेखा मानें, जिसमें $\mathrm{B}$ को शून्य, $\mathrm{C}$ को 1, और इसी तरह। $\mathrm{B}$ को केंद्र और $\mathrm{BD}$ को त्रिज्या मानकर एक चाप खींचें, जो संख्या रेखा को $\mathrm{E}$ पर काटता है (देखें चित्र 1.13)। तब, E, $\sqrt{x}$ को दर्शाता है।

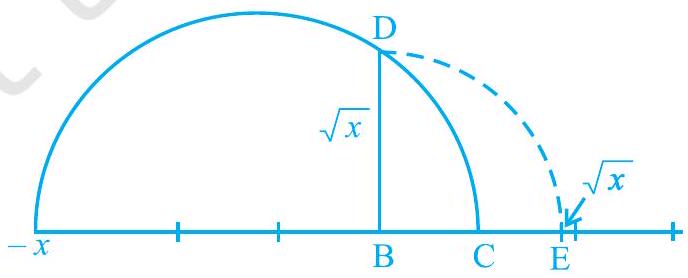
चित्र 1.13

हम अब वर्गमूल के विचार को घनमूल, चतुर्थमूल और सामान्यतः $n$वें मूल तक बढ़ाना चाहेंगे, जहाँ $n$ एक धनात्मक पूर्णांक है। अपनी पिछली कक्षाओं से वर्गमूल और घनमूल की अपनी समझ को याद कीजिए।

$\sqrt[3]{8}$ क्या है? खैर, हम जानते हैं कि यह कोई धनात्मक संख्या होनी चाहिए जिसका घन 8 है, और आपने अनुमान लगाया होगा $\sqrt[3]{8}=2$। आइए $\sqrt[5]{243}$ की कोशिश करें। क्या आपको कोई ऐसी संख्या $b$ पता है कि $b^{5}=243$ हो? उत्तर है 3। इसलिए, $\sqrt[5]{243}=3$।

इन उदाहरणों से, क्या आप $a>0$ वास्तविक संख्या और धनात्मक पूर्णांक $n$ के लिए $\sqrt[n]{a}$ को परिभाषित कर सकते हैं?

मान लीजिए $a>0$ एक वास्तविक संख्या है और $n$ एक धनात्मक पूर्णांक है। तब $\sqrt[n]{a}=b$, यदि $b^{n}=a$ और $b>0$। ध्यान दें कि चिह्न ’ $\sqrt{ }$ ’ जो $\sqrt{2}, \sqrt[3]{8}, \sqrt[n]{a}$ आदि में प्रयुक्त होता है, उसे मूल चिह्न कहा जाता है।

हम अब वर्गमूल से संबंधित कुछ सर्वसमिकाओं की सूची दे रहे हैं, जो विभिन्न प्रकार से उपयोगी हैं। इनमें से कुछ आप पहले से ही अपनी पिछली कक्षाओं से परिचित हैं। शेष वास्तविक संख्याओं के योग पर गुणा के वितरण नियम से और सर्वसमिका $(x+y)(x-y)=x^{2}-y^{2}$ से प्राप्त होती हैं, जहाँ $x$ और $y$ कोई वास्तविक संख्याएँ हैं।

मान लीजिए $a$ और $b$ धनात्मक वास्तविक संख्याएँ हैं। तब

(i) $\sqrt{a b}=\sqrt{a} \sqrt{b}$

(ii) $\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$

(iii) $(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})=a-b$

(iv) $(a+\sqrt{b})(a-\sqrt{b})=a^{2}-b$

(v) $(\sqrt{a}+\sqrt{b})(\sqrt{c}+\sqrt{d})=\sqrt{a c}+\sqrt{a d}+\sqrt{b c}+\sqrt{b d}$

(vi) $(\sqrt{a}+\sqrt{b})^{2}=a+2 \sqrt{a b}+b$

आइए इन सर्वसमिकाओं के कुछ विशिष्ट उदाहरणों को देखें।

उदाहरण 15 : निम्नलिखित व्यंजकों को सरल कीजिए:

(i) $(5+\sqrt{7})(2+\sqrt{5})$

(ii) $(5+\sqrt{5})(5-\sqrt{5})$

(iii) $(\sqrt{3}+\sqrt{7})^{2}$

(iv) $(\sqrt{11}-\sqrt{7})(\sqrt{11}+\sqrt{7})$

हल : (i) $(5+\sqrt{7})(2+\sqrt{5})=10+5 \sqrt{5}+2 \sqrt{7}+\sqrt{35}$

(ii) $(5+\sqrt{5})(5-\sqrt{5})=5^{2}-(\sqrt{5})^{2}=25-5=20$

(iii) $(\sqrt{3}+\sqrt{7})^{2}=(\sqrt{3})^{2}+2 \sqrt{3} \sqrt{7}+(\sqrt{7})^{2}=3+2 \sqrt{21}+7=10+2 \sqrt{21}$

(iv) $(\sqrt{11}-\sqrt{7})(\sqrt{11}+\sqrt{7})=(\sqrt{11})^{2}-(\sqrt{7})^{2}=11-7=4$

टिप्पणी : ध्यान दें कि उपरोक्त उदाहरण में ‘सरल’ शब्द का अर्थ है कि व्यंजक को एक परिमेय और एक अपरिमेय संख्या के योग के रूप में लिखा जाए।

हम इस खंड को निम्नलिखित समस्या पर विचार करके समाप्त करते हैं। $\frac{1}{\sqrt{2}}$ को देखिए। क्या आप बता सकते हैं कि यह संख्या रेखा पर कहाँ स्थित है? आप जानते हैं कि यह अपरिमेय है। शायद यह आसान होगा यदि हर परिमेय संख्या हो। आइए देखें कि क्या हम हर को ‘परिमेय’ बना सकते हैं, अर्थात् हर को एक परिमेय संख्या में बदल सकते हैं। ऐसा करने के लिए, हमें वर्गमूल से संबंधित सर्वसमिकाओं की आवश्यकता है। आइए देखें कि कैसे।

उदाहरण 16 : $\frac{1}{\sqrt{2}}$ का हर परिमेय कीजिए।

हल: हम $\frac{1}{\sqrt{2}}$ को एक समतुल्य व्यंजक के रूप में लिखना चाहते हैं जिसमें हर एक परिमेय संख्या हो। हम जानते हैं कि $\sqrt{2} \cdot \sqrt{2}$ परिमेय है। हम यह भी जानते हैं कि $\frac{1}{\sqrt{2}}$ को $\frac{\sqrt{2}}{\sqrt{2}}$ से गुणा करने पर हमें एक समतुल्य व्यंजक मिलेगा, क्योंकि $\frac{\sqrt{2}}{\sqrt{2}}=1$। इसलिए, हम इन दोनों तथ्यों को एक साथ रखकर प्राप्त करते हैं

$$ \frac{1}{\sqrt{2}}=\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}=\frac{\sqrt{2}}{2} $$

इस रूप में, संख्या रेखा पर $\frac{1}{\sqrt{2}}$ को खोजना आसान है। यह 0 और $\sqrt{2}$ के ठीक बीच में है।

उदाहरण 17: $\frac{1}{2+\sqrt{3}}$ के हर को परिमेय बनाइए।

हल: हम पहले दी गई पहचान (iv) का उपयोग करते हैं। $\frac{1}{2+\sqrt{3}}$ को $2-\sqrt{3}$ से गुणा और भाग देने पर हमें प्राप्त होता है

$$\frac{1}{2+\sqrt{3}} \times \frac{2-\sqrt{3}}{2-\sqrt{3}}=\frac{2-\sqrt{3}}{4-3}=2-\sqrt{3}$$।

उदाहरण 18: $\frac{5}{\sqrt{3}-\sqrt{5}}$ के हर को परिमेय बनाइए।

हल: यहाँ हम पहले दी गई पहचान (iii) का उपयोग करते हैं।

इसलिए, $\frac{5}{\sqrt{3}-\sqrt{5}}=\frac{5}{\sqrt{3}-\sqrt{5}} \times \frac{\sqrt{3}+\sqrt{5}}{\sqrt{3}+\sqrt{5}}=\frac{5(\sqrt{3}+\sqrt{5})}{3-5}=\left(\frac{-5}{2}\right)(\sqrt{3}+\sqrt{5})$

उदाहरण 19: $\frac{1}{7+3 \sqrt{2}}$ के हर को परिमेय बनाइए।

हल: $\frac{1}{7+3 \sqrt{2}}=\frac{1}{7+3 \sqrt{2}} \times\left(\frac{7-3 \sqrt{2}}{7-3 \sqrt{2}}\right)=\frac{7-3 \sqrt{2}}{49-18}=\frac{7-3 \sqrt{2}}{31}$

इसलिए, जब किसी व्यंजक के हर में वर्गमूल वाला पद (या रेडिकल चिह्न के नीचे संख्या) होता है, तो उसे समतुल्य ऐसे व्यंजक में बदलने की प्रक्रिया जिसका हर एक परिमेय संख्या हो, हर का परिमेयकरण कहलाता है।

1.5 वास्तविक संख्याओं के घातांकों के नियम

क्या आपको याद है कि निम्नलिखित को कैसे सरल करना है?

(i) $17^{2} \cdot 17^{5}=$

(ii) $\left(5^{2}\right)^{7}=$

(iii) $\frac{23^{10}}{23^{7}}=$

(iv) $7^{3} \cdot 9^{3}=$

क्या आपको ये उत्तर मिले? वे इस प्रकार हैं:

(i) $17^{2} \cdot 17^{5}=17^{7}$

(ii) $\left(5^{2}\right)^{7}=5^{14}$

(iii) $\frac{23^{10}}{23^{7}}=23^{3}$

(iv) $7^{3} \cdot 9^{3}=63^{3}$

इन उत्तरों को पाने के लिए, आपने घातांकों के निम्नलिखित नियमों का प्रयोग किया होगा, जो आपने अपनी पिछली कक्षाओं में सीखे हैं। (यहाँ $a, n$ और $m$ प्राकृत संख्याएँ हैं। याद रखें, $a$ को आधार कहा जाता है और $m$ तथा $n$ घातांक हैं।)

(i) $a^{m} \cdot a^{n}=a^{m+n}$

(ii) $\left(a^{m}\right)^{n}=a^{m n}$

(iii) $\frac{a^{m}}{a^{n}}=a^{m-n}, m>n$

(iv) $a^{m} b^{m}=(a b)^{m}$

$(a)^{0}$ क्या है? हाँ, यह 1 है! इसलिए आपने सीखा है कि $(a)^{0}=1$। इसलिए, (iii) का प्रयोग करके, हम $\frac{1}{a^{n}}=a^{-n}$ प्राप्त कर सकते हैं। अब हम नियमों को ऋणात्मक घातांकों तक भी बढ़ा सकते हैं।

इसलिए, उदाहरण के लिए:

(i) $17^{2} \cdot 17^{-5}=17^{-3}=\frac{1}{17^{3}}$

(ii) $\left(5^{2}\right)^{-7}=5^{-14}$

(iii) $\frac{23^{-10}}{23^{7}}=23^{-17}$

(iv) $(7)^{-3} \cdot(9)^{-3}=(63)^{-3}$

मान लीजिए हम निम्नलिखित गणनाएँ करना चाहते हैं:

(i) (2^{\frac{2}{3}} \cdot 2^{\frac{1}{3}})

(ii) (\left(3^{\frac{1}{5}}\right)^{4})

(iii) (\frac{7^{\frac{1}{5}}}{7^{\frac{1}{3}}})

(iv) (13^{\frac{1}{5}} \cdot 17^{\frac{1}{5}})

हम इसे कैसे करें? यह पता चलता है कि हम घातांकों के उन नियमों को आगे बढ़ा सकते हैं जो हमने पहले पढ़े हैं, यहाँ तक कि जब आधार एक धनात्मक वास्तविक संख्या हो और घातांक परिमेय संख्याएँ हों। (बाद में आप पढ़ेंगे कि इसे और आगे बढ़ाया जा सकता है जब घातांक वास्तविक संख्याएँ हों।) लेकिन इससे पहले कि हम ये नियम कहें, और इन नियमों का अर्थ भी समझें, हमें पहले यह समझना होगा कि, उदाहरण के लिए, (4^{\frac{3}{2}}) क्या है। तो, हमें कुछ काम करना है!

हम (\sqrt[n]{a}) को एक वास्तविक संख्या (a>0) के लिए इस प्रकार परिभाषित करते हैं:

मान लीजिए (a>0) एक वास्तविक संख्या है और (n) एक धनात्मक पूर्णांक है। तब (\sqrt[n]{a}=b), यदि (b^{n}=a) और (b>0)।

घातांकों की भाषा में, हम (\sqrt[n]{a}=a^{\frac{1}{n}}) परिभाषित करते हैं। तो, विशेष रूप से, (\sqrt[3]{2}=2^{\frac{1}{3}})। अब (4^{\frac{3}{2}}) को देखने के दो तरीके हैं।

[ \begin{aligned} & 4^{\frac{3}{2}}=\left(4^{\frac{1}{2}}\right)^{3}=2^{3}=8 \ & 4^{\frac{3}{2}}=\left(4^{3}\right)^{\frac{1}{2}}=(64)^{\frac{1}{2}}=8 \end{aligned} $$

इसलिए, हमारे पास निम्नलिखित परिभाषा है:

मान लीजिए (a>0) एक वास्तविक संख्या है। मान लीजिए (m) और (n) पूर्णांक हैं इस प्रकार कि (m) और (n) में 1 के अलावा कोई उभयनिष्ठ गुणनखंड नहीं है, और (n>0)। तब,

(a^{\frac{m}{n}}=(\sqrt[n]{a})^{m}=\sqrt[n]{a^{m}})

अब हमारे पास घातांकों के निम्नलिखित विस्तारित नियम हैं:

मान लीजिए $a>0$ एक वास्तविक संख्या है और $p$ तथा $q$ परिमेय संख्याएँ हैं। तब, हमारे पास

(i) $a^{p} \cdot a^{q}=a^{p+q}$

(ii) $\left(a^{p}\right)^{q}=a^{p q}$

(iii) $\frac{a^{p}}{a^{q}}=a^{p-q}$

(iv) $a^{p} b^{p}=(a b)^{p}$

अब आप इन नियमों का उपयोग पहले पूछे गए प्रश्नों के उत्तर देने के लिए कर सकते हैं।

उदाहरण 20 : सरल कीजिए (i) $2^{\frac{2}{3}} \cdot 2^{\frac{1}{3}}$

(ii) $\left(3^{\frac{1}{5}}\right)^{4}$

(iii) $\frac{7^{\frac{1}{5}}}{7^{\frac{1}{3}}}$

(iv) $13^{\frac{1}{5}} \cdot 17^{\frac{1}{5}}$

हल : (i) $2^{\frac{2}{3}} \cdot 2^{\frac{1}{3}}=2^{\left(\frac{2}{3}+\frac{1}{3}\right)}=2^{\frac{3}{3}}=2^{1}=2$

(ii) $\left(3^{\frac{1}{5}}\right)^{4}=3^{\frac{4}{5}}$

(iii) $\frac{7^{\frac{1}{5}}}{7^{\frac{1}{3}}}=7^{\left(\frac{1}{5}-\frac{1}{3}\right)}=7^{\frac{3-5}{15}}=7^{\frac{-2}{15}}$

(iv) $13^{\frac{1}{5}} \cdot 17^{\frac{1}{5}}=(13 \times 17)^{\frac{1}{5}}=221^{\frac{1}{5}}$

1.6 सारांश

इस अध्याय में, आपने निम्नलिखित बिंदुओं का अध्ययन किया है:

1. एक संख्या $r$ को परिमेय संख्या कहा जाता है, यदि इसे $\frac{p}{q}$ के रूप में लिखा जा सकता है, जहाँ $p$ और $q$ पूर्णांक हैं और $q \neq 0$।

2. एक संख्या $s$ को अपरिमेय संख्या कहा जाता है, यदि इसे $\frac{p}{q}$ के रूप में नहीं लिखा जा सकता है, जहाँ $p$ और $q$ पूर्णांक हैं और $q \neq 0$।

3. एक परिमेय संख्या का दशमलव विस्तार या तो सांत होता है या असांत आवर्ती होता है। इसके अतिरिक्त, एक संख्या जिसका दशमलव विस्तार सांत या असांत आवर्ती होता है, वह परिमेय होती है।

4. एक अपरिमेय संख्या का दशमलव विस्तार अनवसानी और अनावर्ती होता है। इसके अतिरिक्त, एक संख्या जिसका दशमलव विस्तार अनवसानी और अनावर्ती होता है, वह अपरिमेय होती है।

5. सभी परिमेय और अपरिमेय संख्याएं मिलकर वास्तविक संख्याओं का समूह बनाती हैं।

6. यदि $r$ परिमेय है और $s$ अपरिमेय है, तो $r+s$ और $r-s$ अपरिमेय संख्याएं होती हैं, और $r s$ और $\frac{r}{s}$ अपरिमेय संख्याएं होती हैं, $r \neq 0$।

7. धनात्मक वास्तविक संख्याओं $a$ और $b$ के लिए, निम्नलिखित सर्वसमिकाएं लागू होती हैं:

(i) $\sqrt{a b}=\sqrt{a} \sqrt{b}$

(ii) $\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$

(iii) $(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})=a-b$

(iv) $(a+\sqrt{b})(a-\sqrt{b})=a^{2}-b$

(v) $(\sqrt{a}+\sqrt{b})^{2}=a+2 \sqrt{a b}+b$

8. $\frac{1}{\sqrt{a}+b}$ के हर को परिमेय बनाने के लिए, हम इसे $\frac{\sqrt{a}-b}{\sqrt{a}-b}$ से गुणा करते हैं, जहां $a$ और $b$ पूर्णांक हैं।

9. मान लीजिए $a>0$ एक वास्तविक संख्या है और $p$ और $q$ परिमेय संख्याएं हैं। तब

(i) $a^{p} \cdot a^{q}=a^{p+q}$

(ii) $\left(a^{p}\right)^{q}=a^{p q}$

(iii) $\frac{a^{p}}{a^{q}}=a^{p-q}$

(iv) $a^{p} b^{p}=(a b)^{p}$