अध्याय 07 मात्राओं की तुलना
7.1 प्रतिशत - मात्राओं की तुलना करने का एक अन्य तरीका
| अनीता की रिपोर्ट |
|---|
| कुल $320 / 400$ |
| प्रतिशत: 80 |
| रीता की रिपोर्ट |
|---|
| कुल $300 / 360$ |
| प्रतिशत: 83.3 |
अनीता ने कहा कि उसने बेहतर प्रदर्शन किया है क्योंकि उसे 320 अंक मिले जबकि रीता को केवल 300 अंक मिले। क्या आप उससे सहमत हैं? आपके विचार से किसने बेहतर प्रदर्शन किया है?
मानसी ने उनसे कहा कि वे केवल प्राप्त कुल अंकों की तुलना करके यह निर्णय नहीं कर सकते कि किसने बेहतर प्रदर्शन किया है क्योंकि जिन अधिकतम अंकों में से उन्हें अंक मिले हैं वे समान नहीं हैं।
उसने कहा कि आप अपनी रिपोर्ट कार्ड में दिए गए प्रतिशत क्यों नहीं देखते?
अनीता का प्रतिशत 80 था और रीता का 83.3 था। तो, इससे पता चलता है कि रीता ने बेहतर प्रदर्शन किया है। क्या आप सहमत हैं?
प्रतिशत भिन्नों के ऐसे अंश होते हैं जिनका हर 100 होता है और इनका उपयोग परिणामों की तुलना में किया जाता है। आइए इसके बारे में विस्तार से समझने का प्रयास करें।
7.1.1 प्रतिशत का अर्थ
प्रतिशत लैटिन शब्द ‘पर सेंटम’ से लिया गया है जिसका अर्थ है ‘प्रति सौ’।
प्रतिशत को प्रतीक $%$ द्वारा दर्शाया जाता है और इसका अर्थ सौवाँ भी होता है। इसका अर्थ है $1 %$
सौ में से 1 या एक सौवाँ होता है। इसे इस प्रकार लिखा जा सकता है: $1 %=\frac{1}{100}=0.01$
इसे समझने के लिए, आइए निम्नलिखित उदाहरण पर विचार करें।
रीना ने 100 विभिन्न रंगों की टाइलों से एक टेबल टॉप बनाया। उसने पीले, हरे, लाल और नीले रंग की टाइलों को अलग-अलग गिना और नीचे दी गई तालिका को भर दिया। क्या आप उसकी तालिका को पूरा करने में मदद कर सकते हैं?
| रंग | टाइलों की संख्या |
प्रति सौ दर |
भिन्न | इस प्रकार लिखा जाता है | इस प्रकार पढ़ा जाता है |
|---|---|---|---|---|---|
| पीला | 14 | 14 | $\frac{14}{100}$ | $14 %$ | 14 प्रतिशत |
| हरा | 26 | 26 | $\frac{26}{100}$ | $26 %$ | 26 प्रतिशत |
| लाल | 35 | 35 | —– | —– | —— |
| नीला | 25 | —– | —– | —– | —– |
| कुल | $\mathbf{1 0 0}$ |
इन्हें आजमाइए
1. निम्नलिखित आंकड़ों के लिए विभिन्न ऊंचाइयों के बच्चों का प्रतिशत ज्ञात कीजिए।
| ऊंचाई | बच्चों की संख्या | भिन्न के रूप में | प्रतिशत के रूप में |
|---|---|---|---|
| $110 ~cm$ | 22 | ||
| $120 ~cm$ | 25 | ||
| $128 ~cm$ | 32 | ||
| $130 ~cm$ | 21 | ||
| कुल | $\mathbf{1 0 0}$ |
2. एक दुकान में विभिन्न आकारों के जूतों की निम्नलिखित संख्या में जोड़ियाँ हैं।
आकार $2: 20$
आकार $3: 30$
आकार $4: 28$
आकार $5: 14$
आकार $6: 8$
इस सूचना को तालिका के रूप में पहले की तरह लिखिए और दुकान में उपलब्ध प्रत्येक जूते के आकार का प्रतिशत ज्ञात कीजिए।
प्रतिशत जब कुल सौ न हो
इन सभी उदाहरणों में वस्तुओं की कुल संख्या 100 है। उदाहरण के लिए, रीना के पास कुल 100 टाइलें थीं, 100 बच्चे थे और 100 जोड़ी जूते थे। यदि वस्तुओं की कुल संख्या 100 नहीं है तो हम किसी वस्तु का प्रतिशत कैसे निकालेंगे? ऐसे मामलों में हमें भिन्न को 100 हर वाले समतुल्य भिन्न में बदलना होता है। निम्नलिखित उदाहरण पर विचार कीजिए। आपके पास दो रंगों की बीस मनियों की एक हार है।
| रंग | मनके की संख्या |
भिन्न | सौ वाला हर | प्रतिशत में |
|---|---|---|---|---|
| लाल | 8 | $\frac{8}{20}$ | $\frac{8}{20} \times \frac{100}{100}=\frac{40}{100}$ | $40 %$ |
| नीला | 12 | $\frac{12}{20}$ | $\frac{12}{20} \times \frac{100}{100}=\frac{60}{100}$ | $60 %$ |
| कुल | $2 0$ |
अनवर ने लाल मनकों का प्रतिशत इस प्रकार निकाला
20 मनकों में से लाल मनकों की संख्या 8 है। इसलिए, 100 में से लाल मनकों की संख्या $\frac{8}{20} \times 100=40($ सौ में से) $=40$%
आशा ने इस प्रकार किया
$ \frac{8}{20}=\frac{8 \times 5}{20 \times 5} $
$=\frac{40}{100}=40$%
हम देखते हैं कि ये तीनों विधियाँ प्रतिशत निकालने के लिए प्रयोग की जा सकती हैं जब कुल 100 नहीं बनता। तालिका में दिखाई गई विधि में हम भिन्न को $\frac{100}{100}$ से गुणा करते हैं। इससे भिन्न का मान नहीं बदलता। बाद में केवल 100 हर में रह जाता है।
अनवर ने एकात्म विधि प्रयोग की है। आशा ने हर में 100 पाने के लिए $\frac{5}{5}$ से गुणा किया है। आप जो विधि उपयुक्त लगे, उसे प्रयोग कर सकते हैं। हो सकता है, आप अपनी खुद की विधि भी बना लें।
अनवार द्वारा प्रयुक्त विधि सभी अनुपातों के लिए काम कर सकती है। क्या आशा द्वारा प्रयुक्त विधि भी सभी अनुपातों के लिए काम कर सकती है? अनवार कहता है कि आशा की विधि तभी प्रयोग की जा सकती है जब आपको कोई प्राकृतिक संख्या मिल सके जिसे हर से गुणा करने पर 100 प्राप्त हो। चूँकि हर 20 था, वह उसे 5 से गुणा कर 100 प्राप्त कर सकी। यदि हर 6 होता, तो वह इस विधि का प्रयोग नहीं कर पाती। क्या आप सहमत हैं?
इन्हें आज़माइए
1. 10 अलग-अलग रंगों की चिप्स का एक संग्रह दिया गया है।
| रंग | संख्या | भिन्न | सौ का हर | प्रतिशत में |
|---|---|---|---|---|
| हरा | ||||
| नीला | ||||
| लाल | ||||
| कुल |
तालिका को भरें और प्रत्येक रंग की चिप्स का प्रतिशत ज्ञात करें।
2. माला के पास चूड़ियों का संग्रह है। उसके पास 20 सोने की चूड़ियाँ और 10 चाँदी की चूड़ियाँ हैं। प्रत्येक प्रकार की चूड़ियों का प्रतिशत क्या है? क्या आप इसे उपरोक्त उदाहरण की तरह सारणीबद्ध रूप में लगा सकते हैं?
सोचिए, चर्चा कीजिए और लिखिए
1. नीचे दिए गए उदाहरणों को देखें और प्रत्येक में चर्चा करें कि तुलना के लिए कौन-सा बेहतर है।
वायुमंडल में, 1 g हवा में होता है:

2. एक कमीज़ में:
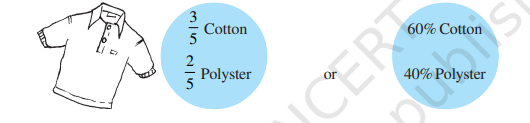
7.1.2 भिन्न संख्याओं को प्रतिशत में बदलना
भिन्न संख्याओं के भिन्न-भिन्न हर हो सकते हैं। भिन्न संख्याओं की तुलना करने के लिए हमें एक समान हर चाहिए होता है और हमने देखा है कि यदि हमारा हर 100 हो तो तुलना करना अधिक सुविधाजनक होता है। अर्थात् हम भिन्नों को प्रतिशत में बदल रहे हैं। आइए विभिन्न भिन्न संख्याओं को प्रतिशत में बदलने का प्रयास करें।
उदाहरण 1 $\frac{1}{3}$ को प्रतिशत के रूप में लिखिए।
हल
हमारे पास, $\frac{1}{3}=\frac{1}{3} \times \frac{100}{100}=\frac{1}{3} \times 100 %$
$ =\frac{100}{3} %=33 \frac{1}{3} % $
उदाहरण 2 एक कक्षा में 25 बच्चों में से 15 लड़कियाँ हैं। लड़कियों का प्रतिशत क्या है?
हल
25 बच्चों में से 15 लड़कियाँ हैं।
इसलिए, लड़कियों का प्रतिशत $=\frac{15}{25} \times 100=60$। कक्षा में $60 %$ लड़कियाँ हैं।
उदाहरण 3 $\frac{5}{4}$ को प्रतिशत में बदलिए।
हल
हमारे पास, $\frac{5}{4}=\frac{5}{4} \times 100 %=125 %$
इन उदाहरणों से हम पाते हैं कि उचित भिन्नों से संबंधित प्रतिशत 100 से कम होते हैं जबकि अनुचित भिन्नों से संबंधित प्रतिशत 100 से अधिक होते हैं।
सोचिए, चर्चा कीजिए और लिखिए
(i) क्या आप एक केक का $50 %$ खा सकते हैं? क्या आप एक केक का $100 %$ खा सकते हैं?
क्या आप एक केक का $150 %$ खा सकते हैं?
(ii) क्या किसी वस्तु की कीमत $50 %$ बढ़ सकती है? क्या किसी वस्तु की कीमत $100 %$ बढ़ सकती है?
क्या किसी वस्तु की कीमत $150 %$ बढ़ सकती है?
7.1.3 दशमलव को प्रतिशत में बदलना
हमने देखा है कि भिन्नों को प्रतिशत में कैसे बदला जाता है। आइए अब जानें कि दशमलव को प्रतिशत में कैसे बदला जाता है।
उदाहरण 4 दिए गए दशमलवों को प्रतिशत में बदलें:
(a) 0.75
(b) 0.09
(c) 0.2
हल
(a) $0.75=0.75 \times 100 %$
(b) $0.09=\frac{9}{100}=9 %$
$ =\frac{75}{100} \times 100 %=75 % $
(c) $0.2=\frac{2}{10} \times 100 %=20 %$
इन्हें आज़माइए
1. निम्नलिखित को प्रतिशत में बदलें:
(a) $\frac{12}{16}$
(b) 3.5
(c) $\frac{49}{50}$
(d) $\frac{2}{2}$
(e) 0.05
2. (i) 32 विद्यार्थियों में से 8 अनुपस्थित हैं। कितने प्रतिशत विद्यार्थी अनुपस्थित हैं?
(ii) 25 रेडियो हैं, उनमें से 16 खराब हैं। कितने प्रतिशत रेडियो खराब हैं?
(iii) एक दुकान में 500 वस्तुएँ हैं, जिनमें से 5 खराब हैं। कितने प्रतिशत खराब हैं?
(iv) 120 मतदाता हैं, उनमें से 90 ने ही वोट दिया। कितने प्रतिशत ने ही वोट दिया?
7.1.4 प्रतिशत को भिन्न या दशमलव में बदलना
हमने अब तक भिन्नों और दशमलवों को प्रतिशत में बदला है। हम इसका उल्टा भी कर सकते हैं। अर्थात्, दिए गए प्रतिशतों को हम दशमलव या भिन्न में बदल सकते हैं। तालिका को देखें, देखें और उसे पूरा करें:
| प्रतिशत | $1 $% | $10 $% | $25 $% | $50 $% | $90 $% | $125 $% | $250$% |
|---|---|---|---|---|---|---|---|
| भिन्न | $\frac{1}{100}$ | $\frac{10}{100}=\frac{1}{10}$ | |||||
| दशमलव | 0.01 | 0.10 |
कुछ और ऐसे उदाहरण बनाओ और उन्हें हल करो।
भाग हमेशा मिलकर पूरा बनाते हैं
रंगीन टाइलों, बच्चों की ऊँचाइयों और वायु में गैसों के उदाहरणों में हम देखते हैं कि जब हम प्रतिशतों को जोड़ते हैं तो हमें 100 प्राप्त होता है। सभी भाग जो पूरे को बनाते हैं, जब एक साथ जोड़े जाते हैं तो पूरा या $100 %$ देते हैं। इसलिए, यदि हमें एक भाग दिया गया हो तो हम हमेशा दूसरा भाग निकाल सकते हैं। मान लीजिए,
दी गई संख्या के छात्रों में से $30 %$% लड़के हैं।
इसका अर्थ है कि यदि 100 छात्र हों तो उनमें से 30 लड़के होंगे और शेष लड़कियाँ होंगी।
तब लड़कियाँ स्पष्ट रूप से $(100-30)%=70%$ होंगी।
इन्हें आज़माओ
1. 35%+_____%=100%,
64%+20%+_____%=100%
45%=100%-_____%
70%=_____%-30%
2. यदि किसी कक्षा के 65 % छात्रों के पास साइकिल है, तो कितने प्रतिशत छात्रों के पास साइकिल नहीं है?
3. हमारे पास सेब, संतरे और आमों से भरी एक टोकरी है। यदि 50 % सेब हैं, 30 % संतरे हैं, तो कितने प्रतिशत आम हैं?
सोचो, चर्चा करो और लिखो
किसी पोशाक पर किए गए व्यय पर विचार करें
$20 %$% कढ़ाई पर, $50 %$% कपड़े पर, $30 %$% सिलाई पर।
क्या आप और ऐसे उदाहरण सोच सकते हैं?
7.1.5 अनुमान के साथ मजा
प्रतिशत हमें किसी क्षेत्र के भागों का अनुमान लगाने में मदद करते हैं।
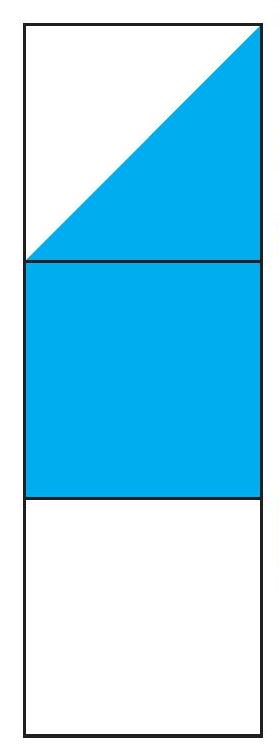
उदाहरण 5 संलग्न आकृति का कितना प्रतिशत भाग छायांकित है?
हल
हम पहले वह भिन्न निकालते हैं जो आकृति का छायांकित भाग है। इस भिन्न से छायांकित भाग का प्रतिशत निकाला जा सकता है।
आप पाएंगे कि आकृति का आधा भाग छायांकित है। और, $\frac{1}{2}=\frac{1}{2} \times 100 =50 $%
इस प्रकार, आकृति का $50$% भाग छायांकित है।
इन्हें आजमाएँ
इन आकृतियों का कितना प्रतिशत भाग छायांकित है?

आप स्वयं कुछ और आकृतियाँ बना सकते हैं और अपने मित्रों से छायांकित भागों का अनुमान लगाने को कह सकते हैं।
7.2 प्रतिशतों का प्रयोग
7.2.1 प्रतिशतों की व्याख्या
हमने देखा कि प्रतिशत तुलना में कितने उपयोगी होते हैं। हमने भिन्न संख्याओं और दशमलवों को प्रतिशत में बदलना भी सीखा है। अब हम सीखेंगे कि प्रतिशत का उपयोग वास्तविक जीवन में कैसे किया जा सकता है। इसके लिए हम निम्नलिखित कथनों की व्याख्या करना शुरू करते हैं:
—-$5 %$% आय का रवि द्वारा बचत किया जाता है। —– मीरा के कपड़ों में से $20 %$% नीले रंग के हैं। —-रेखा को हर किताब बेचने पर $10 %$% मिलता है।
आप इनमें से प्रत्येक कथन से क्या निष्कर्ष निकाल सकते हैं?
$5 %$% से हमारा तात्पर्य 100 में से 5 भाग है या हम इसे $\frac{5}{100}$ लिखते हैं। इसका अर्थ है कि रवि हर ₹ 100 में से ₹ 5 बचाता है। इसी तरह, ऊपर दिए गए बाकी कथनों की व्याख्या करें।
7.2.2 प्रतिशत को “कितने” में बदलना
निम्नलिखित उदाहरणों पर विचार करें:
उदाहरण 6 40 बच्चों के एक सर्वेक्षण से पता चला कि $25 %$ को फुटबॉल खेलना पसंद है। कितने बच्चों को फुटबॉल खेलना पसंद है?
हल
यहाँ, कुल बच्चों की संख्या 40 है। इनमें से, $25 %$ को फुटबॉल खेलना पसंद है। मीना और अरुण ने संख्या ज्ञात करने के लिए निम्नलिखित विधियों का उपयोग किया। आप कोई भी विधि चुन सकते हैं।
अरुण इसे इस तरह करता है
100 में से, 25 को फुटबॉल खेलना पसंद है
इसलिए 40 में से, बच्चों की संख्या जो
फुटबॉल खेलना पसंद करते हैं $=\frac{25}{100} \times 40=10$
मीना इसे इस तरह करती है
$25 %$ का $40=\frac{25}{100} \times 40$
$=10$
इसलिए, 40 में से 10 बच्चों को फुटबॉल खेलना पसंद है।
इन्हें आज़माएँ
1. ज्ञात करें:
(a) $50 %$% का 164
(b) $75 %$% का 12
(c) $12 \frac{1}{2} %$% का 64
2. 25 बच्चों की एक कक्षा के $8 %$% बच्चे बारिश में भीगना पसंद करते हैं। कितने बच्चे बारिश में भीगना पसंद करते हैं।
उदाहरण 7 राहुल ने एक स्वेटर खरीदा और $25 %$% की छूट मिलने पर ₹ 200 बचाए। छूट से पहले स्वेटर की कीमत क्या थी?
हल
राहुल ने ₹ 200 बचाए जब स्वेटर की कीमत $25 %$% घटाई गई। इसका अर्थ है कि कीमत में $25 %$% की कमी राहुल द्वारा बचाई गई राशि है। आइए देखें कि मोहन और अब्दुल ने स्वेटर की मूल लागत कैसे ज्ञात की।
मोहन का हल
मूल कीमत का $25 %$% = ₹ 200
माना कीमत (₹ में) $P$ है
इसलिए, $P$ का $25 %$% = 200 या $\frac{25}{100} \times P=200$
या, $\frac{P}{4}=200$ या $P=200 \times 4$
अतः, $P=800$
अब्दुल का हल
प्रत्येक ₹ 100 पर ₹ 25 बचत
वह राशि जिस पर ₹ 200 बचत हुई
$ =\frac{100}{25} \times 200=₹ 800 $
इस प्रकार दोनों ने स्वेटर की मूल कीमत ₹ 800 प्राप्त की।
इन्हें आज़माइए
- 9 किस संख्या का $25 %$% है?
- किस संख्या का $75 %$% 15 है?
अभ्यास 7.1
1. दिए गए भिन्नीय संख्याओं को प्रतिशत में बदलिए।
(a) $\frac{1}{8}$
(b) $\frac{5}{4}$
(c) $\frac{3}{40}$
(d) $\frac{2}{7}$
2. दिए गए दशमलव भिन्नों को प्रतिशत में बदलिए।
(a) 0.65
(b) 2.1
(c) 0.02
(d) 12.35
3. अनुमान लगाइए कि आकृतियों का कितना भाग रंगा गया है और इससे रंगे गए प्रतिशत को ज्ञात कीजिए।
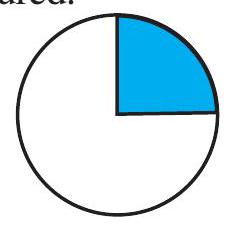
(i)
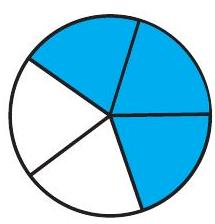
(ii)
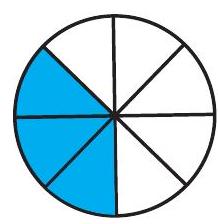
(iii)
4. ज्ञात कीजिए:
(a) 250 का 15%
(b) 1 घंटे का 1%
(c) ₹ 2500 का 20%
(d) 1 kg का 75%
5. पूरी मात्रा ज्ञात कीजिए यदि
(a) उसका 5% 600 है।
(b) उसका 12% ₹ 1080 है।
(c) उसका 40% 500 km है।
(d) उसका 70% 14 मिनट है।
(e) उसका 8% 40 लीटर है।
6. दिए गए प्रतिशतों को दशमलव भिन्नों में और सरलतम रूप के भिन्नों में भी बदलिए:
(a) 25%
(b) 150%
(c) 20%
(d) 5%
7. एक शहर में 30% महिलाएँ हैं, 40% पुरुष हैं और शेष बच्चे हैं। कितने प्रतिशत बच्चे हैं?
8. एक निर्वाचन क्षेत्र के 15,000 मतदाताओं में से 60% ने मतदान किया। उन मतदाताओं का प्रतिशत ज्ञात कीजिए जिन्होंने मतदान नहीं किया। क्या आप अब बता सकते हैं कि वास्तव में कितनों ने मतदान नहीं किया?
9. मीता अपने वेतन से ₹4000 बचाती है। यदि यह उसके वेतन का 10% है। उसका वेतन कितना है?
10. एक स्थानीय क्रिकेट टीम ने एक सीज़न में 20 मैच खेले। उसने उनमें से 25% मैच जीते। उन्होंने कितने मैच जीते?
7.2.3 अनुपात से प्रतिशत
कभी-कभी भाग हमें अनुपात के रूप में दिए जाते हैं और हमें उन्हें प्रतिशत में बदलना होता है। निम्नलिखित उदाहरण पर विचार करें:
उदाहरण 8 रीना की माँ ने कहा, इडली बनाने के लिए तुम्हें दो भाग चावल और एक भाग उड़द दाल लेनी चाहिए। ऐसे मिश्रण में चावल का कितना प्रतिशत होगा और उड़द दाल का कितना प्रतिशत होगा?
हल
अनुपात के रूप में हम इसे चावल : उड़द दाल = 2 : 1 लिखेंगे।
अब, 2 + 1 = 3 सभी भागों का योग है। इसका अर्थ है कि (\frac{2}{3}) भाग चावल है और (\frac{1}{3}) भाग उड़द दाल है।
फिर, चावल का प्रतिशत होगा (\frac{2}{3} \times 100) % = (\frac{200}{3} = 66\frac{2}{3}) %।
उड़द दाल का प्रतिशत होगा (\frac{1}{3} \times 100) % = (\frac{100}{3} = 33\frac{1}{3}) %।
उदाहरण 9 यदि ₹250 को रवि, राजू और रॉय में इस प्रकार बाँटना है कि रवि को दो भाग, राजू को तीन भाग और रॉय को पाँच भाग मिलें। प्रत्येक को कितना पैसा मिलेगा? यह प्रतिशत में क्या होगा?
हल
तीनों लड़कों को मिलने वाले भागों को अनुपात के रूप में 2 : 3 : 5 लिखा जा सकता है। भागों का योग 2 + 3 + 5 = 10 है।
| प्रत्येक को प्राप्त राशि | प्रत्येक के लिए धन का प्रतिशत |
|---|---|
| $\frac{2}{10} \times ₹ 250=₹ 50$ | $\text{ रवि को मिलता है } \frac{2}{10} \times$ 100 %=20% |
| $\frac{3}{10} \times ₹ 250=₹ 75$ | $\text{ राजू को मिलता है } \frac{3}{10} \times$ 100 %=30 |
| $\frac{5}{10} \times ₹ 250=₹ 125$ | $\text{ रॉय को मिलता है } \frac{5}{10} \times$ 100 %=50 |
इन्हें आज़माइए
1. 15 मिठाइयों को मनु और सोनू में इस प्रकार बाँटें कि उन्हें क्रमशः $20 %$% और $80 %$% मिलें।
2. यदि एक त्रिभुज के कोण $2: 3: 4$ के अनुपात में हैं। तो प्रत्येक कोण का मान ज्ञात कीजिए।
7.2.4 प्रतिशत के रूप में वृद्धि या कमी
ऐसे समय होते हैं जब हमें किसी निश्चित मात्रा में वृद्धि या कमी को प्रतिशत के रूप में जानने की आवश्यकता होती है। उदाहरण के लिए, यदि किसी राज्य की जनसंख्या 5,50,000 से बढ़कर $6,05,000$ हो गई। तो जनसंख्या में वृद्धि को बेहतर रूप से समझा जा सकता है यदि हम कहें कि जनसंख्या $10 %$ बढ़ी।
हम किसी मात्रा में वृद्धि या कमी को प्रारंभिक राशि के प्रतिशत के रूप में कैसे परिवर्तित करते हैं? निम्नलिखित उदाहरण पर विचार कीजिए।
उदाहरण 10 एक स्कूल की टीम ने इस वर्ष 6 खेल जीते जबकि पिछले वर्ष 4 खेल जीते। प्रतिशत वृद्धि क्या है?
हल
जीतों की संख्या में वृद्धि (या परिवर्तन की मात्रा) $=6-4=2$।
$ \begin{aligned} \text{ प्रतिशत वृद्धि } & =\frac{\text{ परिवर्तन की मात्रा }}{\text{ मूल राशि या आधार }} \times 100 \\ & =\frac{\text{ जीतों की संख्या में वृद्धि }}{\text{ जीतों की मूल संख्या }} \times 100=\frac{2}{4} \times 100=50 \end{aligned} $
उदाहरण 11 एक देश में निरक्षर व्यक्तियों की संख्या 10 वर्षों में 150 लाख से घटकर 100 लाख हो गई। कितने प्रतिशत की कमी हुई?
हल
मूल राशि $=$ प्रारंभ में निरक्षर व्यक्तियों की संख्या $=150$ लाख।
परिवर्तन की राशि $=$ निरक्षर व्यक्तियों की संख्या में कमी $=150-100=50$ लाख इसलिए, प्रतिशत कमी
$ =\frac{\text{ परिवर्तन की राशि }}{\text{ मूल राशि }} \times 100=\frac{50}{150} \times 100=33 \frac{1}{3} $
इन्हें आज़माइए
1. वृद्धि या कमी का प्रतिशत ज्ञात कीजिए:
- कमीज़ का मूल्य ₹ 280 से घटकर ₹ 210 हो गया।
- परीक्षा में अंक 20 से बढ़कर 30 हो गए।
2. मेरी माँ कहती हैं कि उसके बचपन में पेट्रोल ₹ 1 प्रति लीटर था। आज यह ₹ 52 प्रति लीटर है। मूल्य में कितने प्रतिशत की वृद्धि हुई है?
7.3 किसी वस्तु से संबंधित कीमतें या खरीद-फरोख्त
मैंने इसे ₹ 600 में खरीदा

किसी भी वस्तु की खरीद कीमत को क्रय मूल्य कहा जाता है। इसे संक्षेप में CP लिखा जाता है। जिस कीमत पर आप बेचते हैं, उसे विक्रय मूल्य या संक्षेप में SP कहा जाता है।
आप क्या कहेंगे कि क्या बेहतर है—वस्तु को अपनी खरीद कीमत से कम, बराबर या अधिक कीमत पर बेचना? आप यह तय कर सकते हैं कि बिक्री लाभदायक थी या नहीं, CP और SP पर निर्भर करता है। यदि CP<SP तो आपने लाभ कमाया $=SP-CP$।
$ \begin{aligned} & \text{ यदि } CP=SP \text{ तो आप न लाभ न हानि की स्थिति में हैं। } \ & \text{ यदि } CP>SP \text{ तो आपको हानि हुई है }=CP-SP \text{। } \end{aligned} $
आइए वस्तुओं की कीमतों से संबंधित कथनों की व्याख्या करने का प्रयास करें।
- एक खिलौना जिसे ₹ 72 में खरीदा गया, ₹ 80 में बेचा गया।
- एक टी-शर्ट जिसे ₹ 120 में खरीदा गया, ₹ 100 में बेची गई।
- एक साइकल जिसे ₹ 800 में खरीदा गया, ₹ 940 में बेची गई।
आइए पहले कथन पर विचार करें।
खरीद मूल्य (या CP) ₹ 72 है और विक्रय मूल्य (या SP) ₹ 80 है। इसका अर्थ है SP, CP से अधिक है। अतः लाभ हुआ $=SP-CP=₹ 80-₹ 72=₹ 8$
अब शेष कथनों की भी इसी प्रकार व्याख्या करने का प्रयास करें।
7.3.1 लाभ या हानि प्रतिशत के रूप में
लाभ या हानि को प्रतिशत में बदला जा सकता है। यह सदैव CP पर ही गणना की जाती है।
उपरोक्त उदाहरणों के लिए हम लाभ $%$ या हानि $%$ निकाल सकते हैं।
आइए खिलौने से संबंधित उदाहरण पर विचार करें। हमारे पास $CP=₹ 72, SP=₹ 80$, लाभ $=₹ 8$ है। लाभ का प्रतिशत ज्ञात करने के लिए, नेहा और शेखर ने निम्नलिखित विधियों का प्रयोग किया है।
नीहा इस तरह करती है
लाभ प्रतिशत=$\frac{\text{लाभ}}{क्रय मूल्य}\times 100=\frac{8}{72}\times 100$
$=\frac{1}{9}\times 100=11\frac{1}{9}$
शेखर इस तरह करता है
₹ 72 पर लाभ ₹ 8 है
₹ 100 पर लाभ=$\frac{8}{72}\times 100$
$=11\frac{1}{9}.$ इस प्रकार, लाभ प्रतिशत $11\frac{1}{9}$
इस प्रकार, लाभ ₹ 8 है और लाभ प्रतिशत $11\frac{1}{9}$ है।
इसी तरह आप दूसरी स्थिति में हानि प्रतिशत निकाल सकते हैं। यहाँ,
$क्रय मूल्य=₹ 120,विक्रय मूल्य=₹ 100.$
इसलिए, हानि =$₹ 120- ₹ 100=₹ 20$
हानि प्रतिशत$=\frac{हानि}{क्रय मूल्य}\times 100$
$=\frac{20}{120}\times 100$
$\frac{50}{3}=16\frac{2}{3}$
₹ 120 पर, हानि ₹ 20 है
$\frac{20}{120}\times 100=\frac{50}{3}=16\frac{2}{3}$
इस प्रकार, हानि प्रतिशत $16\frac{2}{3}$ है
अंतिम स्थिति को आज़माएँ।
अब हम देखते हैं कि मूल्यों से संबंधित तीन राशियों में से किन्हीं दो को देने पर, अर्थात् क्रय मूल्य, विक्रय मूल्य, लाभ या हानि की राशि या उनका प्रतिशत, हम शेष को निकाल सकते हैं।
उदाहरण 12 एक फूलदान का क्रय मूल्य ₹ 120 है। यदि दुकानदार इसे $10 %$ की हानि पर बेचता है, तो ज्ञात कीजिए कि यह किस मूल्य पर बेचा गया।
हल
हमें दिया गया है कि $क्रय मूल्य=₹ 120$ और हानि प्रतिशत $=10$। हमें विक्रय मूल्य ज्ञात करना है।
सोहन इस तरह करता है
$10 %$ की हानि का अर्थ है यदि क्रय मूल्य ₹ 100 है, तो हानि ₹ 10 है
इसलिए, विक्रय मूल्य होगा
$₹(100-10)=₹ 90$
जब क्रय मूल्य ₹ 100 है, विक्रय मूल्य ₹ 90 है।
इसलिए, यदि क्रय मूल्य ₹ 120 होता तो
$विक्रय मूल्य=\frac{90}{100} \times 120=₹ 108$
आनंदी इस तरह करती है
हानि क्रय मूल्य का $10 %$ है
$ \begin{aligned} & =₹ 120 का 10 % \\ & =\frac{10}{100} \times 120=₹ 12 \end{aligned} $
इसलिए $ \begin{aligned} SP & =CP-\text{ हानि } \\ & =₹ 120-₹ 12=₹ 108 \end{aligned} $
इस प्रकार, दोनों विधियों से हमें SP ₹ 108 प्राप्त होता है।
उदाहरण 13 एक खिलौने की कार का विक्रय मूल्य ₹ 540 है। यदि दुकानदार द्वारा किया गया लाभ $20 %$ है, तो इस खिलौने का क्रय मूल्य क्या है?
हल
हमें दिया गया है कि $SP=₹ 540$ और लाभ $=20 %$। हमें CP ज्ञात करना है।
| अमीना इसे इस प्रकार करती है |
|---|
| $20 %$ लाभ का अर्थ होगा यदि $CP$ ₹ 100 है, |
| लाभ ₹ 20 है |
| इसलिए, $SP=100+20=120$ |
| अब, जब $SP$ ₹ 120 है, |
| तब $CP$ ₹ 100 है। |
| इसलिए, जब $SP$ ₹ 540 है, |
| तब $CP=\frac{100}{120} \times 540=₹ 450$ |
| अरुण इसे इस प्रकार करता है |
|---|
| लाभ $=CP$ का $20 %$ और $SP=CP+$ लाभ |
| इसलिए, $540=CP+CP$ का $20 %$ |
| $=CP+\frac{20}{100} \times CP=[1+\frac{1}{5}] CP$ |
| $=\frac{6}{5} CP$. इसलिए, $540 \times \frac{5}{6}=CP$ |
| या ₹ 450=CP |
इस प्रकार, दोनों विधियों से, क्रय मूल्य ₹ 450 है।
इन्हें आजमाइए
1. एक दुकानदार ने एक कुर्सी ₹ 375 में खरीदी और ₹ 400 में बेच दी। लाभ प्रतिशत ज्ञात कीजिए।
2. एक वस्तु की लागत ₹ 50 है। इसे $12 %$ लाभ के साथ बेचा गया। विक्रय मूल्य ज्ञात कीजिए।
3. एक वस्तु को ₹ 250 में $5 %$ लाभ के साथ बेचा गया। इसका क्रय मूल्य क्या था?
4. एक वस्तु को ₹ 540 में $5 %$ हानि के साथ बेचा गया। इसका क्रय मूल्य क्या था?
7.4 उधार लिए गए धन पर लगाया गया शुल्क या साधारण ब्याज
सोहिनी ने कहा कि वे एक नया स्कूटर खरीदने जा रहे हैं। मोहन ने उससे पूछा कि क्या उनके पास उसे खरीदने के लिए पैसे हैं। सोहिनी ने कहा कि उसके पिता बैंक से ऋण लेने जा रहे हैं। जो पैसे उधार लिए जाते हैं उन्हें उधार राशि या मूलधन कहा जाता है।
यह पैसा उधारकर्ता कुछ समय तक उपयोग करेगा और फिर वापस करेगा। इस पैसे को कुछ समय तक रखने के लिए उधारकर्ता को बैंक को कुछ अतिरिक्त पैसे देने होते हैं। इसे ब्याज कहा जाता है।
आप वह राशि ज्ञात कर सकते हैं जो आपको वर्ष के अंत में देनी होगी, उधार राशि और ब्याज को जोड़कर। अर्थात्, राशि = मूलधन + ब्याज।
ब्याज आमतौर पर एक वर्ष की अवधि के लिए प्रतिशत में दिया जाता है। इसे $10 %$% प्रति वर्ष या प्रति वर्षम या संक्षेप में $10 %$% p.a. (प्रति वर्षम) लिखा जाता है।
$10 %$% p.a. का अर्थ है हर ₹ 100 उधार पर, ₹ 10 ब्याज है जो आपको एक वर्ष के लिए देना होता है। आइए एक उदाहरण लेते हैं और देखते हैं कि यह कैसे काम करता है।
उदाहरण 14 अनीता ₹ 5,000 का ऋण $15 %$% प्रति वर्ष की ब्याज दर पर लेती है। वह एक वर्ष के अंत में देने वाले ब्याज को ज्ञात कीजिए।
हल
उधार ली गई राशि $=₹ 5,000$, ब्याज दर $=15 %$% प्रति वर्ष।
इसका अर्थ है कि अगर ₹ 100 उधार लिए जाते हैं, तो उसे एक वर्ष के लिए ₹ 15 ब्याज के रूप में देना होता है। अगर उसने ₹ 5,000 उधार लिए हैं, तो एक वर्ष के लिए देने वाला ब्याज
$ =₹ \frac{15}{100} \times 5000=₹ 750 $
इसलिए, वर्ष के अंत में उसे ₹ $5,000+₹ 750=₹ 5,750$ की राशि देनी होगी।
हम एक वर्ष के लिए ब्याज ज्ञात करने के लिए एक सामान्य संबंध लिख सकते हैं। मूलधन या राशि को $P$ लें और वार्षिक दर प्रतिशत को $R %$ लें।
अब हर ₹ 100 उधार लेने पर, ₹ $R$ ब्याज देना होता है।
इसलिए, ₹ $P$ उधार लेने पर, एक वर्ष के लिए देय ब्याज $\frac{R \times P}{100}=\frac{P \times R}{100}$ होगा।
7.4.1 बहु-वर्षीय ब्याज
यदि राशि एक वर्ष से अधिक समय के लिए उधार ली जाती है, तो ब्याज उस अवधि के लिए गणना किया जाता है जितने समय के लिए धन रखा जाता है। उदाहरण के लिए, यदि अनीता दो वर्ष के अंत में धन वापस करती है और ब्याज दर वही है, तो उसे दोगुना ब्याज देना होगा अर्थात् पहले वर्ष ₹ 750 और दूसरे वर्ष ₹ 750। ब्याज की इस विधि, जहाँ मूलधन नहीं बदला जाता, साधारण ब्याज कहलाती है। जैसे-जैसे वर्षों की संख्या बढ़ती है, ब्याज भी बढ़ता है। ₹ 100 को 3 वर्षों के लिए $18 %$ पर उधार लेने पर, 3 वर्ष के अंत में देय ब्याज $18+18+18=3 \times 18=₹ 54$ होगा।
हम एक वर्ष से अधिक समय के लिए साधारण ब्याज का सामान्य रूप ज्ञात कर सकते हैं।
हम जानते हैं कि ₹ $P$ मूलधन पर $R %$ वार्षिक ब्याज दर से, एक वर्ष के लिए देय ब्याज $\frac{R \times P}{100}$ होता है। इसलिए, $T$ वर्षों के लिए देय ब्याज $I$
$ \frac{T \times R \times P}{100}=\frac{P \times R \times T}{100} \text{ या } \frac{P R T}{100} $
और $T$ वर्षों के अंत में आपको देय राशि $A=P+I$ होगी।
इन्हें आज़माइए
1. ₹ 10,000 को $5 %$ वार्षिक ब्याज दर पर निवेशित किया गया है। एक वर्ष के अंत में ब्याज ज्ञात कीजिए।
२. ₹ 3,500 को $7 %$ प्रति वर्ष की ब्याज दर पर दिया गया है। दो वर्ष के अंत में प्राप्त होने वाला ब्याज ज्ञात कीजिए।
३. ₹ 6,050 को $6.5 %$ प्रति वर्ष की ब्याज दर पर उधार लिया गया है। 3 वर्ष के अंत में देय ब्याज और राशि ज्ञात कीजिए।
४. ₹ 7,000 को $3.5 %$ प्रति वर्ष की ब्याज दर पर 2 वर्ष के लिए उधार लिया गया है। दूसरे वर्ष के अंत में देय राशि ज्ञात कीजिए।
जैसे वस्तुओं से संबंधित कीमतों के मामले में, यदि आपको संबंध $I=\frac{P \times T \times R}{100}$ में तीन मात्राओं में से कोई दो दी गई हों, तो आप शेष मात्रा ज्ञात कर सकते हैं।
उदाहरण 15 यदि मनोहर ₹ 4,500 की राशि पर 2 वर्ष के लिए ₹ 750 ब्याज देता है, तो ब्याज दर ज्ञात कीजिए।
| हल 1 | हल 2 |
|---|---|
| $P \times T \times R$ | 2 वर्षों के लिए, दिया गया ब्याज $₹ 750$ है |
| $1=\frac{100}{10}$ | इसलिए, 1 वर्ष के लिए, दिया गया ब्याज $₹ \underline{750}=₹ 375$ है |
| इसलिए, $750=\frac{4500 \times 2 \times R}{100}$ | ₹ 4,500 पर, दिया गया ब्याज ₹ 375 है |
| या $\quad \frac{750}{45 \times 2}=R^{100}$ | इसलिए, ₹ 100 पर, दी गई ब्याज दर |
| इसलिए, दर $=8 \frac{1}{3} %$ | $=\frac{375 \times 100}{4500}=8 \frac{1}{3} %$ |
इन्हें आज़माइए
1. आपके खाते में $₹ 2,400$ हैं और ब्याज दर $5 %$ है। कितने वर्षों के बाद आपको ₹ 240 ब्याज प्राप्त होगा।
2. एक निश्चित राशि पर 3 वर्ष के बाद दिया गया ब्याज $₹ 450$ है जबकि ब्याज दर $5 %$ प्रति वर्ष है। राशि ज्ञात कीजिए।
अभ्यास 7.2
1. निम्नलिखित लेन-देनों में लाभ या हानि बताएं। साथ ही प्रत्येक स्थिति में लाभ प्रतिशत या हानि प्रतिशत भी ज्ञात कीजिए।
(a) बागवानी कैंची ₹ 250 में खरीदी गई और ₹ 325 में बेची गई।
(b) एक रेफ्रिजरेटर ₹ 12,000 में खरीदा गया और ₹ 13,500 में बेचा गया।
(c) एक अलमारी ₹ 2,500 में खरीदी गई और ₹ 3,000 में बेची गई।
(d) एक स्कर्ट ₹ 250 में खरीदी गई और ₹ 150 में बेची गई।
2. अनुपात के प्रत्येक भाग को प्रतिशत में बदलें:
(a) $3: 1$
(b) $2: 3: 5$
(c) $1: 4$
(d) $1: 2: 5$
3. एक शहर की जनसंख्या 25,000 से घटकर 24,500 हो गई। प्रतिशत कमी ज्ञात कीजिए।
4. अरुण ने एक कार ₹ $3,50,000$ में खरीदी। अगले वर्ष, कीमत बढ़कर $₹ 3,70,000$ हो गई। कीमत में प्रतिशत वृद्धि कितनी थी?
5. मैं एक टी.वी. ₹ 10,000 में खरीदता हूँ और उसे $20 %$% के लाभ पर बेचता हूँ। मुझे उसके लिए कितना धन मिलता है?
6. जूही एक वॉशिंग मशीन ₹ 13,500 में बेचती है। उसे इस सौदे में $20 %$% की हानि होती है। वह इसे किस कीमत पर खरीदी थी?
7. (i) चॉक में कैल्शियम, कार्बन और ऑक्सीजन 10:3:12 के अनुपात में होते हैं। चॉक में कार्बन का प्रतिशत ज्ञात कीजिए।
(ii) यदि चॉक की एक स्टिक में कार्बन $3 g$ है, तो चॉक स्टिक का वजन कितना है?
8. अमीना एक किताब ₹ 275 में खरीदती है और उसे $15 %$% की हानि पर बेचती है। वह इसे कितने में बेचती है?
9. प्रत्येक स्थिति में 3 वर्षों के अंत में देय राशि ज्ञात कीजिए:
(a) मूलधन $=₹ 1,200$ जिसकी दर $12 %$% प्रति वर्ष है।
(b) मूलधन $=₹ 7,500$ जिसकी दर $5 %$% प्रति वर्ष है।
10. ₹ 56,000 की राशि पर 2 वर्षों में ₹ 280 ब्याज देने वाली दर कितनी है?
११. यदि मीना एक वर्ष के लिए ₹ 45 ब्याज $9 %$% वार्षिक दर से देती है, तो उसने कितनी राशि उधार ली है?
हमने क्या चर्चा की है?
१. मात्राओं की तुलना का एक तरीका प्रतिशत है। प्रतिशत, 100 हर वाली भिन्नों के अंश होते हैं। प्रतिशत का अर्थ है प्रति सौ।
उदाहरण के लिए $82 %$ अंक का अर्थ है सौ में से 82 अंक।
२. भिन्नों को प्रतिशत में और प्रतिशत को भिन्न में बदला जा सकता है।
उदाहरण के लिए, $\frac{1}{4}=\frac{1}{4} \times 100 %$% जबकि, 75%$=\frac{75}{100}=\frac{3}{4}$
३. दशमलवों को भी प्रतिशत में और प्रतिशत को दशमलव में बदला जा सकता है।
उदाहरण के लिए, $0.25=0.25 \times 100 $%==25%
४. प्रतिशत हमारे दैनिक जीवन में व्यापक रूप से प्रयोग किए जाते हैं,
(क) हमने सीखा है कि कुल मात्रा का एक निश्चित प्रतिशत दिया गया हो तो वास्तविक संख्या कैसे निकाली जाए।
(ख) जब किसी मात्रा के भाग अनुपात के रूप में दिए जाते हैं, तो हमने देखा है कि उन्हें प्रतिशत में कैसे बदला जाए।
(ग) किसी निश्चित मात्रा में वृद्धि या कमी को भी प्रतिशत के रूप में व्यक्त किया जा सकता है।
(घ) किसी निश्चित लेन-देन में हुआ लाभ या हानि को प्रतिशत के पदों में व्यक्त किया जा सकता है।
(ङ) जब कोई राशि उधार ली जाती है तो उस पर ब्याज की गणना करते समय ब्याज की दर प्रतिशत के रूप में दी जाती है। उदाहरण के लिए, ₹ 800 को 3 वर्षों के लिए $12 %$ वार्षिक दर से उधार लिया गया।











